算法DAY52 动态规划10 300.最长递增子序列 674. 最长连续递增序列 718. 最长重复子数组

news2024/11/18 3:42:34

300.最长递增子序列

五部曲：
1、dp数组的含义：
dp[ i ] : 代表截至到nums[i] (包括 nums[i]) 的序列中，以nums[i] 结尾的，最长递增子序列的长度。这里强调以nums[i] 结尾，是因为还要跟nums[j]做对比，确定是不是递增的。
2、递推公式
if(nums[i] > nums[j]) dp = max(dp[i],dp[j]+1)
注意：dp[i] 随着j可能会变化多次，所以其实是在取满足条件的 dp[j]+1的最大值
3、初始化
对于每一个单独的nums[i]，连续子序列都是1
4、遍历顺序
j从0~i-1，无所谓前后。但是dp[i] 依赖于dp[i-1]，所以必须从前向后遍历
5、举例推导
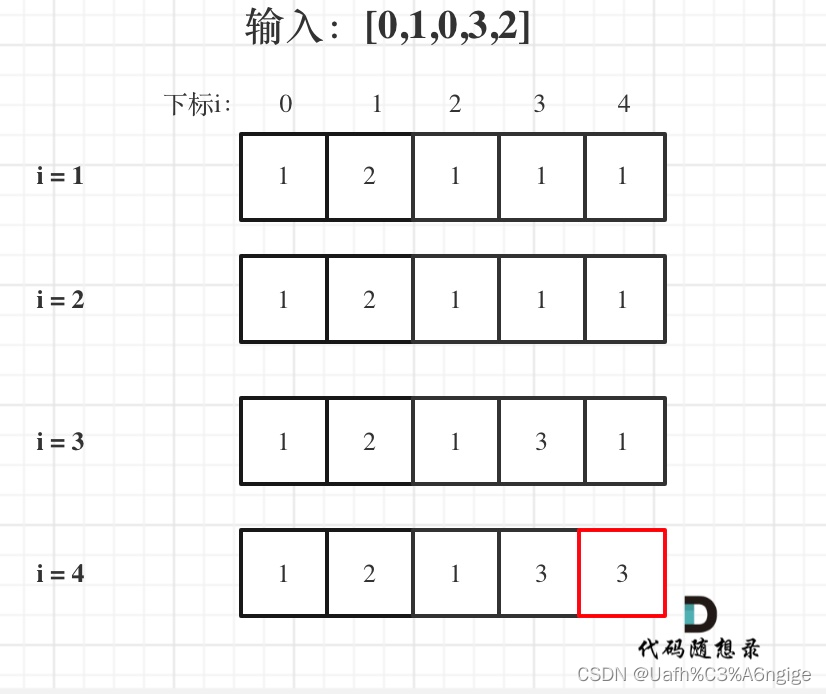
在这里插入图片描述

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        vector<int> dp(nums.size(),1);
        int res = 0;
        for(int i = 1; i < nums.size(); ++i){
            for(int j = 0; j < i; ++j){
                if(nums[i] > nums[j])dp[i] = max(dp[i],dp[j]+1);
            }
            if(dp[i] > res) res = dp[i];
        }

        return res == 0 ? 1 : res;
    }
};

674. 最长连续递增序列

本题可以直接用暴力写出来。

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        int res = 0;
        int count = 1;
        for(int i = 1; i< nums.size(); ++i ){
            if(nums[i] > nums[i-1]){
                count++;
                if(count > res) res = count;
                continue;
            }
            else{
                count = 1;
            }
            
        }
        return res == 0 ? 1 : res;
    }
};

动态规划：
1、dp[i] : 以nums[i]结尾的序列，最长连续递增子序列的长度
2、递推公式
因为要是连续子序列，所以只能是当dp[i] > dp[i-1] 时，dp[i] = dp[i-1] + 1;
3、初始化
都是1
4、遍历顺序
从前向后

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        vector<int> dp(nums.size(),1);
        int res = 1;
        for(int i = 1; i < nums.size(); ++i){
            if(nums[i] > nums[i-1]) dp[i] = dp[i-1] + 1;
            if(dp[i] > res) res = dp[i];
        }
        return res;
    }
};

718. 最长重复子数组

1、dp[i][j] : 以A[i-1], B[j-1]为结尾的A B字符串的最大重复子序列。
不定义成以A[i], B[j]为结尾的A B字符串的最大重复子序列，是因为会多一步初始化的步骤，如果nums1[i] 与 nums2[0] 相同的话，对应的 dp[i][0]就要初始为1，因为此时最长重复子数组为1。 nums2[j] 与 nums1[0]相同的话，同理。

// 要对第一行，第一列经行初始化
        for (int i = 0; i < nums1.size(); i++) if (nums1[i] == nums2[0]) dp[i][0] = 1;
        for (int j = 0; j < nums2.size(); j++) if (nums1[0] == nums2[j]) dp[0][j] = 1;

而以A[i-1], B[j-1]为结尾的A B字符串的最大重复子序列这种定义里，dp[i][0], dp[0][j] 是无意义的。但是依然需要初始化为0，因为会依赖i-1，j-1。假设A[0] = B[0]，dp[1][1] = dp[0][0] + 1。

不太好理解，还是看：以A[i], B[j]为结尾的A B字符串的最大重复子序列，这个定义。
2、递推公式

if (nums1[i] == nums2[j] && i > 0 && j > 0) { // 防止 i-1 出现负数
    dp[i][j] = dp[i - 1][j - 1] + 1;
}

3、初始化
在定义中已经提及
4、遍历顺序
从前向后

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>> dp(nums1.size(),vector<int>(nums2.size() , 0));
        for(int i = 0; i< nums1.size();i++) {
            if(nums2[0] == nums1[i]){
                dp[i][0] = 1;
            }
        }
        for(int j = 0; j< nums2.size();j++) {
            if(nums1[0] == nums2[j]){
                dp[0][j] = 1;
            }
        }
        int res = 0;
        for(int i = 0; i < nums1.size();++i){
            for(int j = 0; j < nums2.size();++j){
                if(nums1[i] == nums2[j] && i>0 && j >0){
                    dp[i][j] = dp[i-1][j-1] + 1;
                }
                if(res < dp[i][j]) res = dp[i][j];
            }
        }
        return res;
    }
};