非递归遍历二叉树
- 前序
- 中序
- 后序
接下来我们在研究如何使用循环实现遍历二叉树时,以下面的二叉树为例:
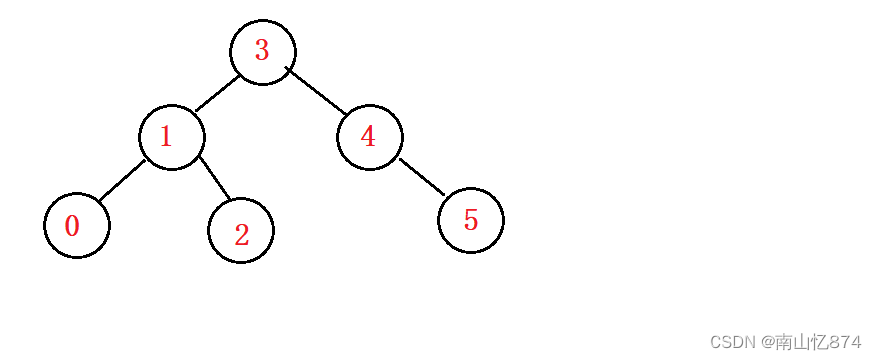
在下文的讲解中,不对如何构建这颗二叉树做讲解,直接给出代码,如果有不懂的地方欢迎私信我。
文章中的完整源代码链接在结尾处。
前序
先来讲解前序。
前序的遍历顺序为:根-左-右,所以以上面的这棵树为例,前序遍历的结果就应该为:3 1 0 2 4 5。
我们要遍历这颗树,不适用递归的话,就只能使用循环的方式来了。
思路讲解:
根据前序的遍历顺序我们不难发现,我们首先要先将根节点和左子树遍历完才能遍历右子树,所以我们可以先循环遍历到这颗树的最左结点,同时将结点的值存放在vector中。如下图所示:
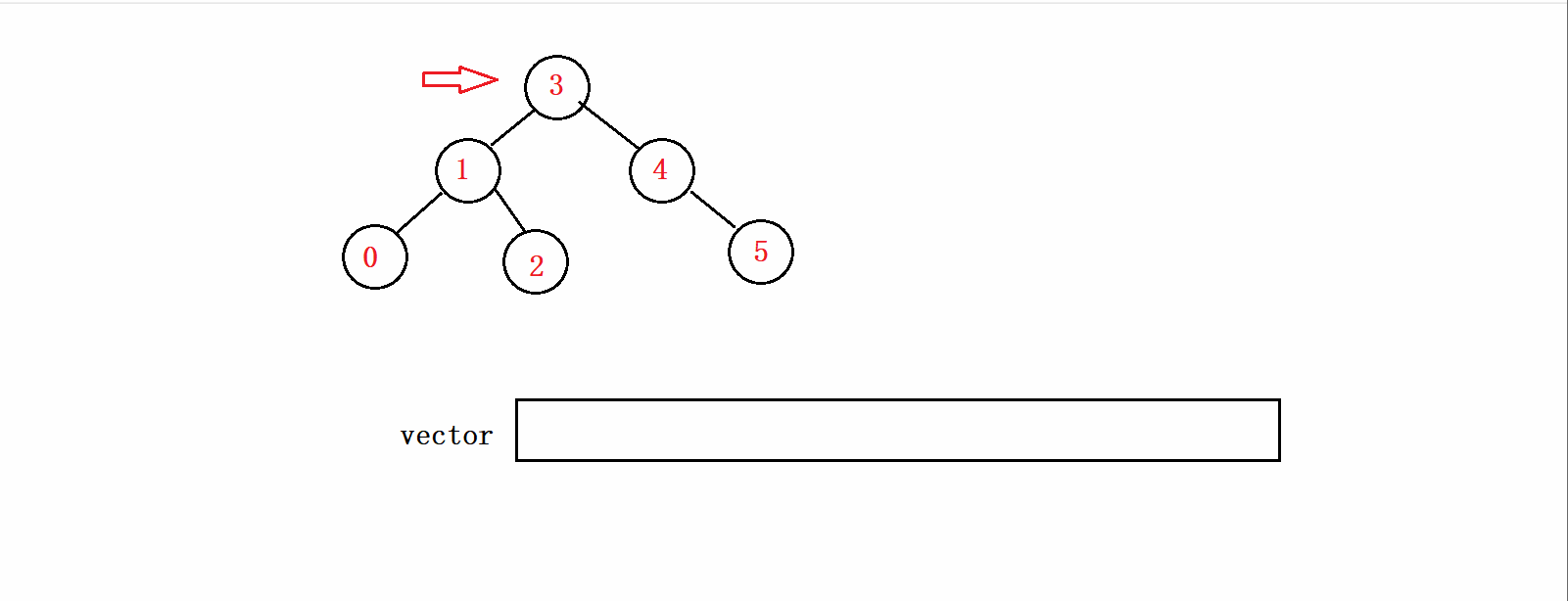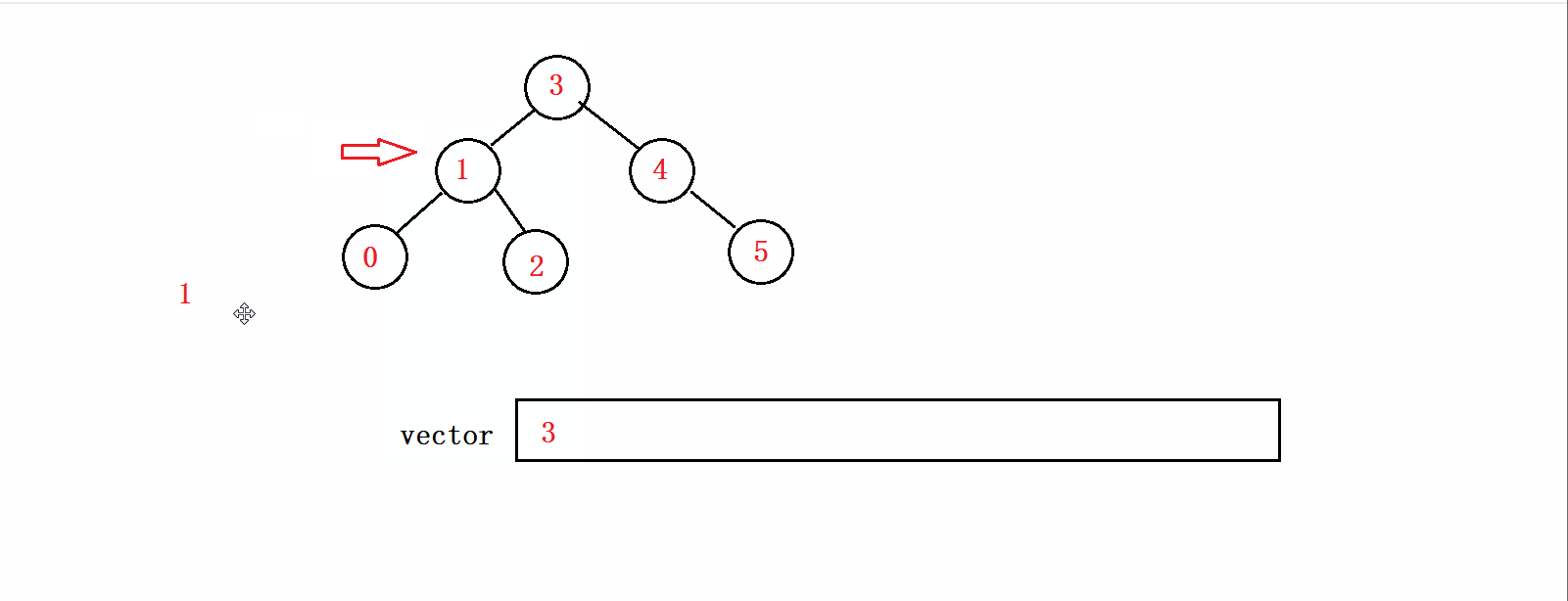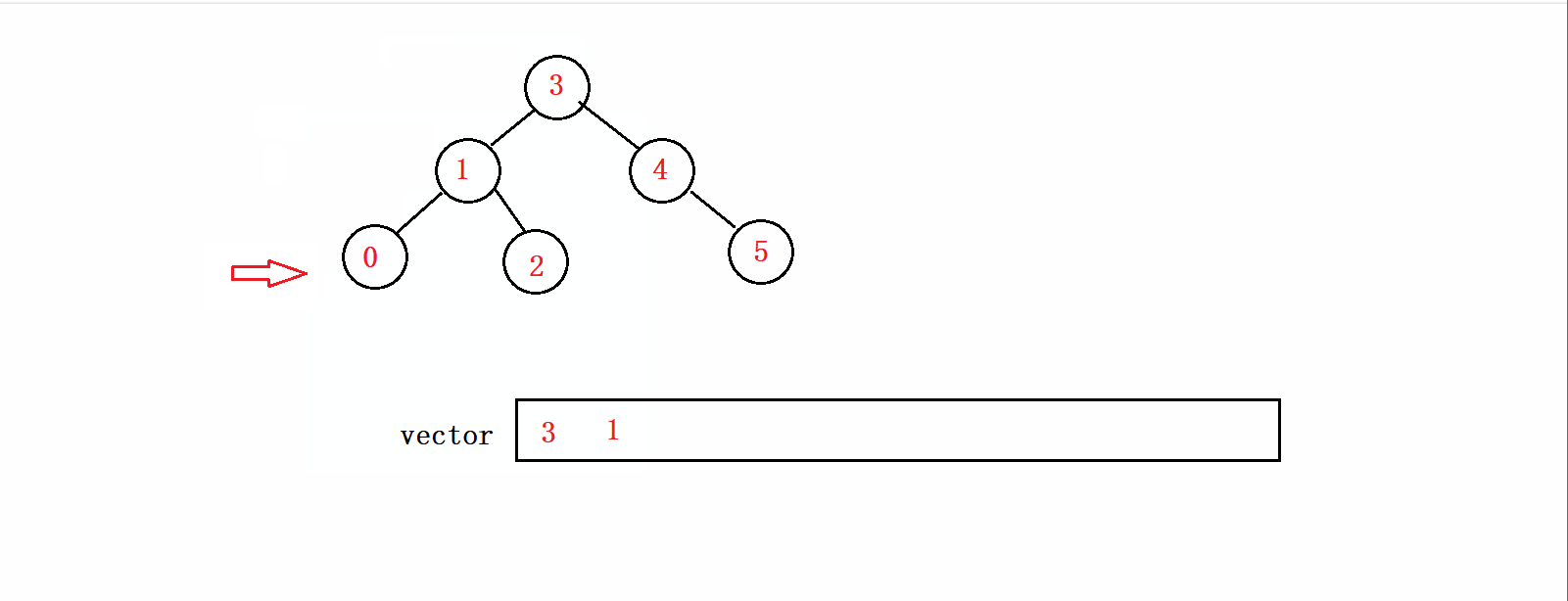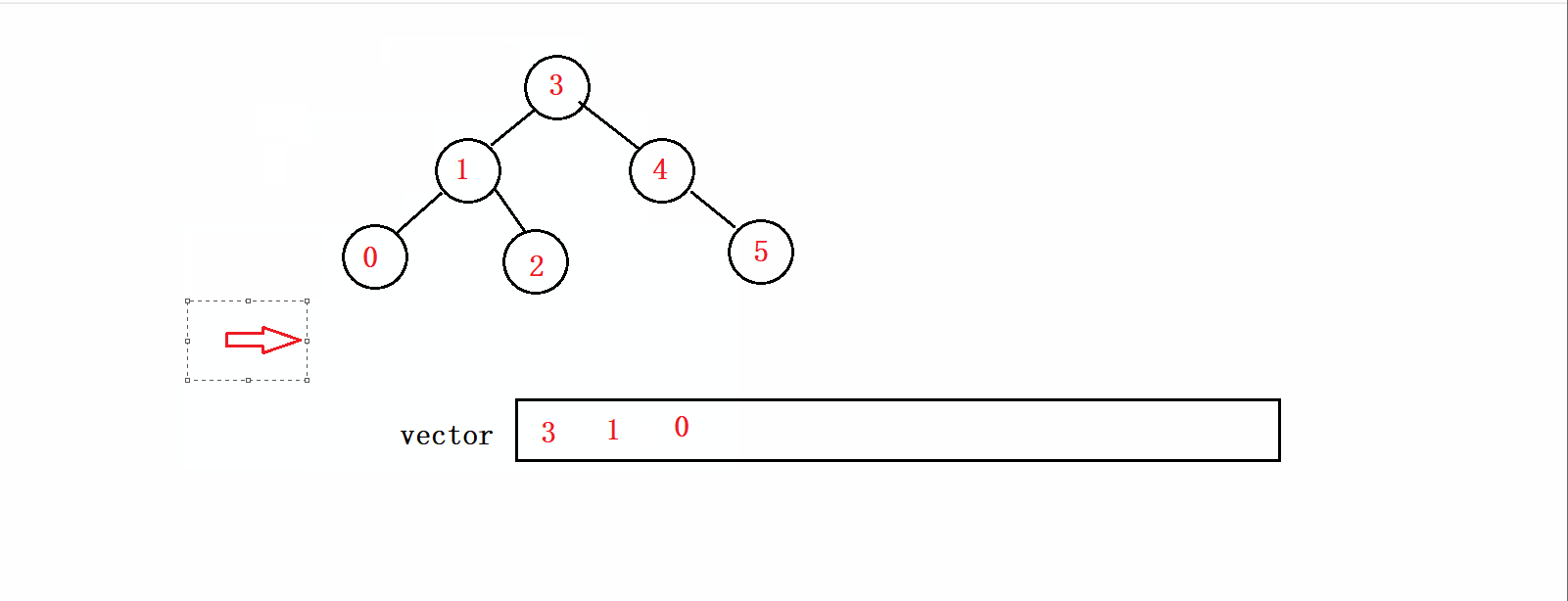
接下来我们就要考虑的是,如何遍历右子树的问题。
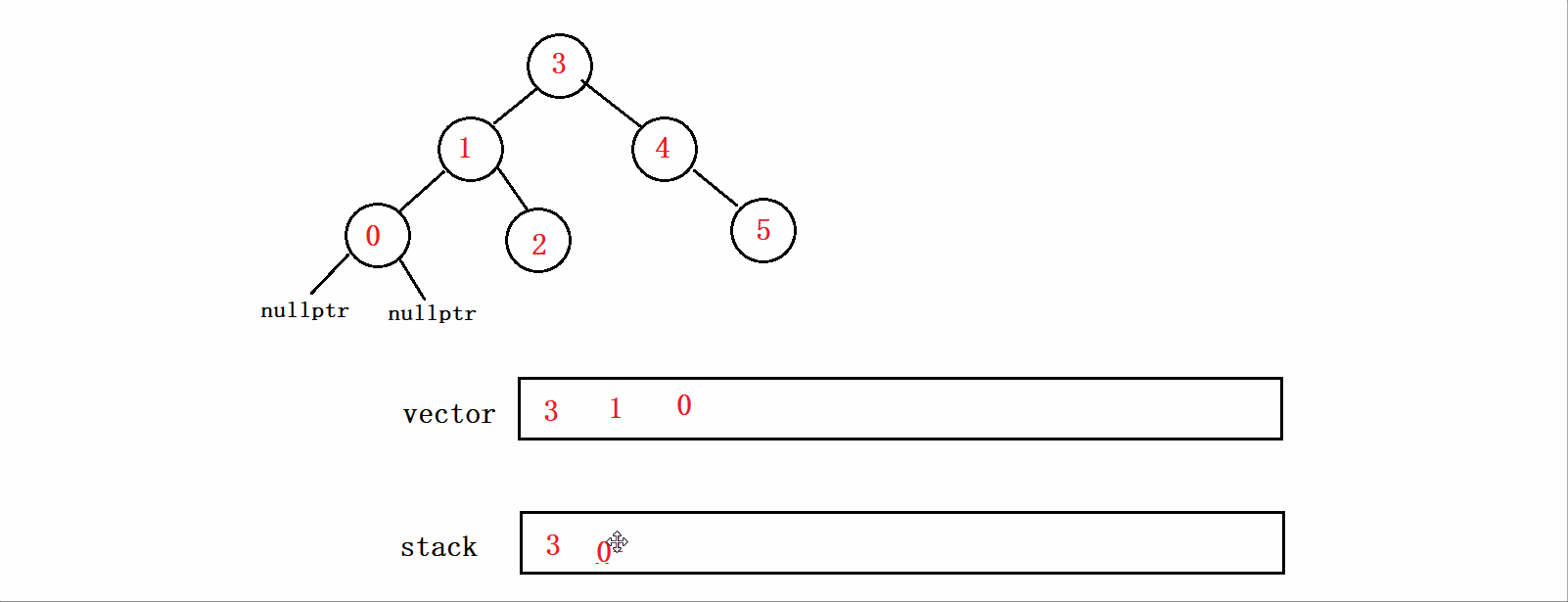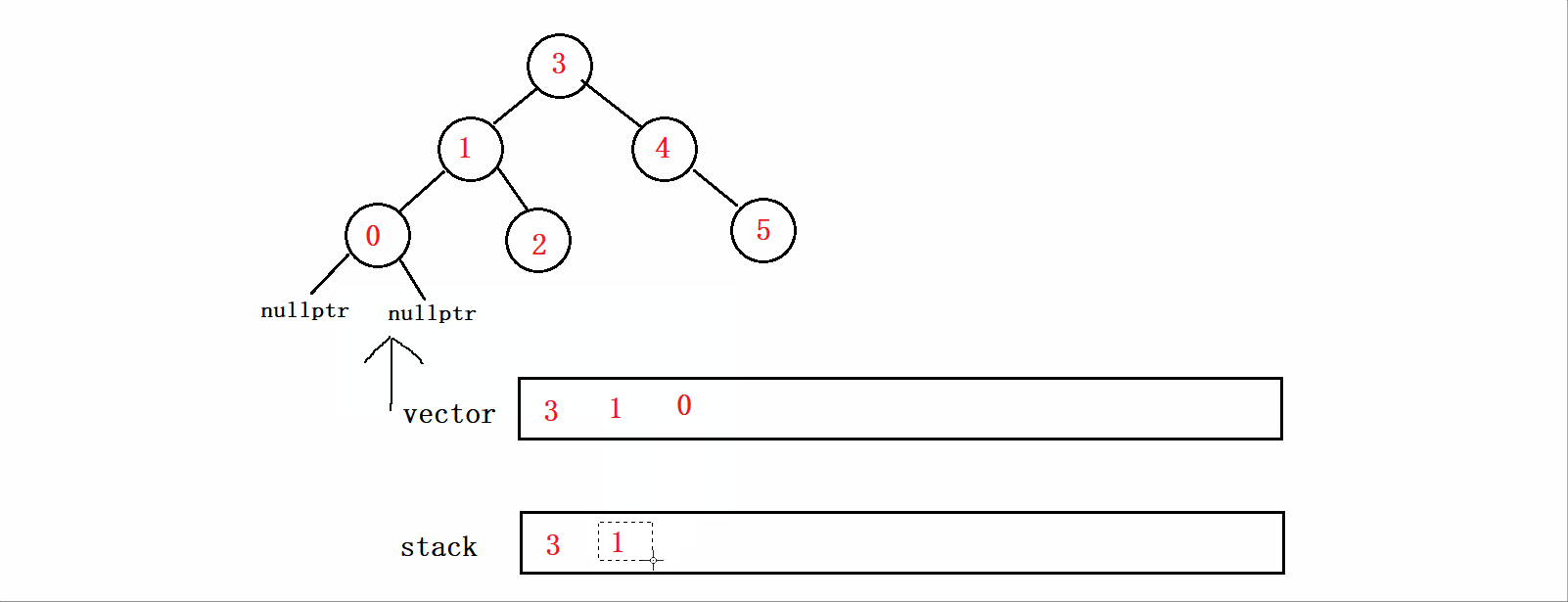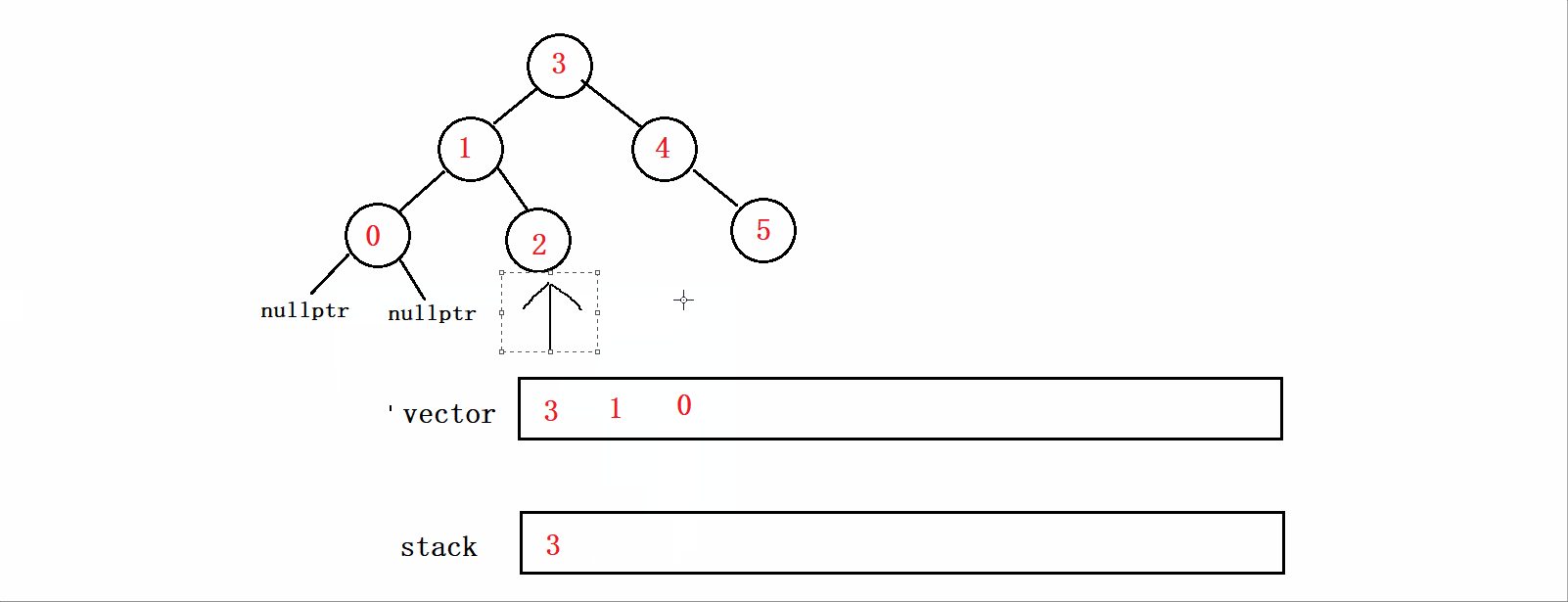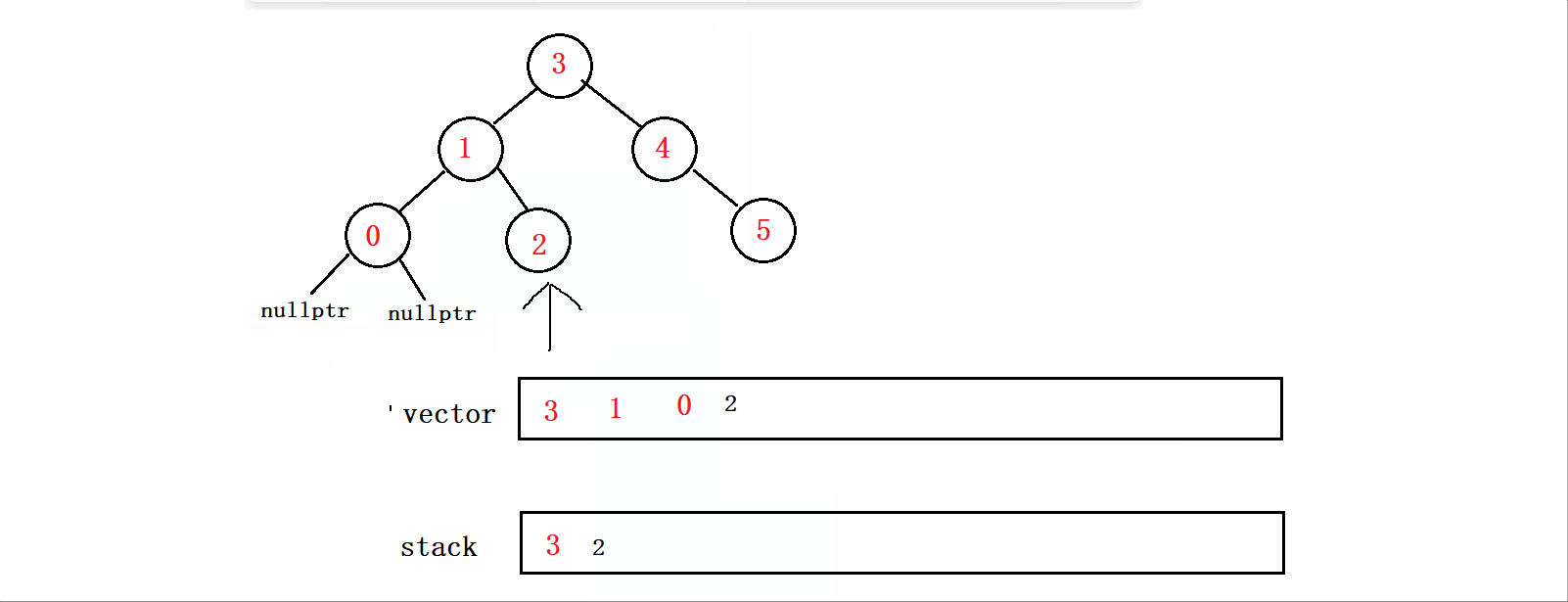
其实也不难,我们只需要使用一个栈,在vector存在结点的值的同时,将结点也存放在栈结构中即可,即在上图的遍历完成后我们还能得到一个下图所示的栈:

在上图中我们已经完成了0结点和0结点的左子树的遍历,因为0结点的左子树为空所以本次循环结束,接下来我们只需要取栈顶元素,即0结点,让栈顶元素的右子树按照同样的方式进行遍历即可。
因为0的右子树也为空,所以下次循环直接结束,再取栈顶元素的时候,因为0已经被取走了,再取就是1结点了,1结点的右子树不为空,所以2入vector和栈。
上诉过程如下图所示:
然后就是以同样的方式去遍历整颗树。
代码如下:
//前序遍历
vector<int> preorderTraversal(TreeNode* root)
{
//非递归,借助栈来实现
//分为两大的问题,一,左路结点, 二,左路节点的右子树
stack<TreeNode*> st;
vector<int> arr;
TreeNode* cur = root;
while (cur || !st.empty())
{
//1.先访问左路结点
while (cur)
{
st.push(cur);
arr.push_back(cur->val);
cur = cur->left;//向左走,先把左路结点全部放到栈
}
//2.开始处理最左结点的右子树问题
TreeNode* top = st.top();
st.pop();
//访问每个左路结点的右子树就是上述过程的子问题,把左节点的第一个右结点
//看成一个树的根节点。
cur = top->right;
}
return arr;
}
测试结果:
中序
中序的遍历和前序本质上没有太大的区别,一定要在理解前序之后再来看中序。
这里先直接给出代码,再给代码进行解释:
//中序遍历
vector<int> inorderTraversal(TreeNode* root) {
//思路跟前序的非递归相似
stack<TreeNode*> st;
vector<int> arr;
TreeNode* cur = root;
while (cur || !st.empty())
{
while (cur)
{
st.push(cur);
cur = cur->left;
}
TreeNode* top = st.top();
st.pop();
arr.push_back(top->val);
cur = top->right;//一个结点从栈中出来就意味着,它和它的左子树访问完了
}
return arr;
}
因为中序遍历的顺序是:左-根-右。
所以在遍历到最左结点的时候,不应该直接入vector中,而是在取栈顶元素的时候,将其值入到vector中去。
认真观察我们可以发现一点:一个结点如果出栈的话,就代表这个结点的左子树肯定是遍历完了的!!
后序
后序就需要先遍历完左右子树再去处理根节点了。
讲解以注释的形式给出了,按照代码的思路去走一遍才能更好的理解。
//后序遍历
vector<int> postorderTraversal(TreeNode* root) {
//思路跟前序的非递归相似
stack<TreeNode*> st;
vector<int> arr;
TreeNode* cur = root;
TreeNode* prev = nullptr;
while (cur || !st.empty())
{
while (cur)
{
st.push(cur);
cur = cur->left;
}
TreeNode* top = st.top();
if (top->right == nullptr || top->right == prev)
{
//满足第一个条件的时候,处理的就是左结点
//满足第二个条件的时候,处理的就是根结点,,在满足第二个条件的时候,就说明左右子树都处理完了
arr.push_back(top->val);
prev = top;
st.pop();
}
else
cur = top->right;//开始遍历右子树
}
return arr;
}
测试结果:
点此处->源代码链接