C++——二叉搜索树

news2024/11/29 20:38:51

目录

二叉搜索树

二叉搜索树实现 

非递归插入|非递归查找

删除 

推导阶段 

非递归删除代码 

递归查找 

 递归插入

递归删除 

析构函数 

拷贝构造 

赋值重载

完整代码 

 二叉搜索树的应用

Key/Value模型 

 

二叉搜索树

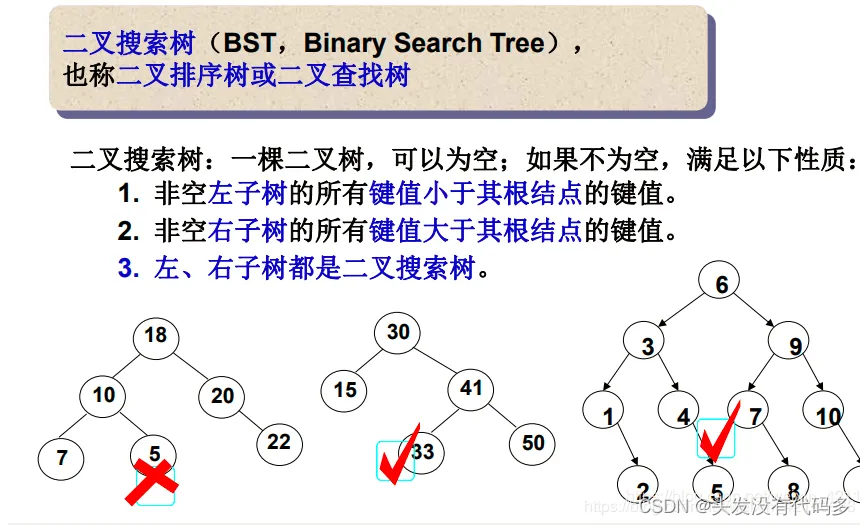
 二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:
    若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
    若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
    它的左右子树也分别为二叉搜索树

二叉搜索树实现 

非递归插入|非递归查找

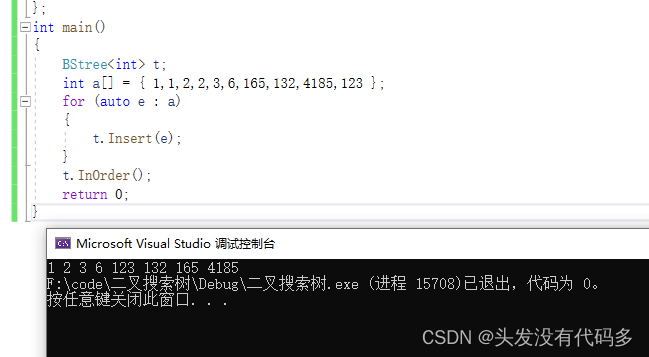
#include<iostream>
using namespace std;
template<class K>
class BStreeNode
{
public:
	BStreeNode(const K& key)
		:_left(nullptr),
		_right(nullptr),
		_key(key)
	{}
	BStreeNode<K>* _left;
	BStreeNode<K>* _right;
	K _key;
};
template<class K>
class BStree
{
	typedef BStreeNode<K> Node;
public:
	bool Insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}

		cur = new Node(key);
		if (parent->_key < key)
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}

		return true;
	}
bool Find(const K& key)//查找
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				cur = cur->_left;
			}
			else
			{
				return true;
			}
		}

		return true;
	}
	void InOrder()
	{
		_InOrder(_root);
	}
private:
	void _InOrder(Node *root)
	{
		if (root == nullptr)
			return;
		_InOrder(root->_left);
		cout << root->_key << " ";
		_InOrder(root->_right);
	}
private:
	Node* _root = nullptr;
};
int main()
{
	BStree<int> t;
	int a[] = { 1,1,2,2,3,6,165,132,4185,123 };
	for (auto e : a)
	{
		t.Insert(e);
	}
	t.InOrder();
	return 0;
}

 

可去重 

删除 

推导阶段 

 1.若要删除的节点是叶子节点，直接删除即可

2.删除节点只有一个孩子

若左为空，则让父亲节点指向该节点的右子树以删除3为例

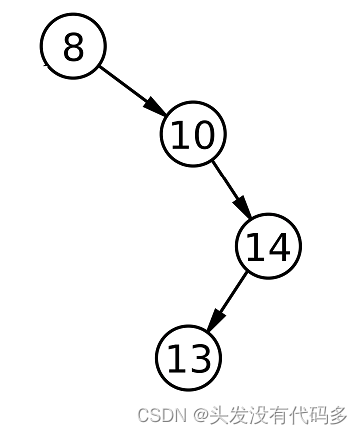
若果要删除跟节点，而且左为空，若要删除8，我们更新根节点即可，让根节点指向10

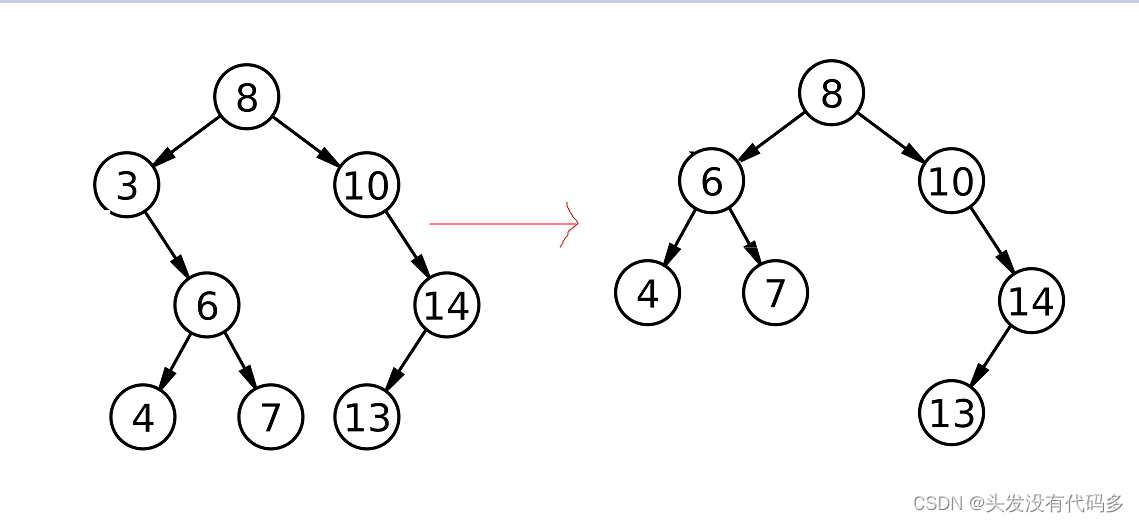
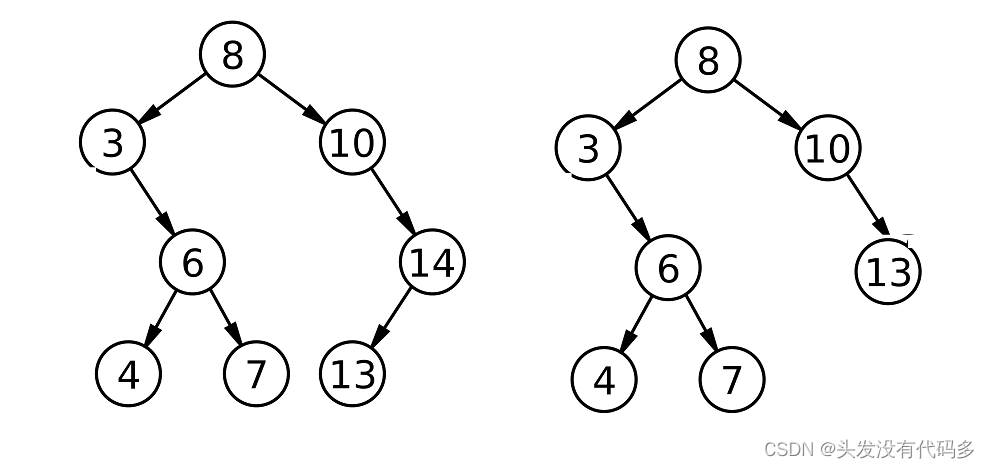
若右为空，则让父亲指向左子树，以删除14为例

  若果要删除跟节点，而且右为空，若要删除8，让根节点指向3即可

 3.要删除的节点其左右节点都不为空

我们可以采用替换法删除节点

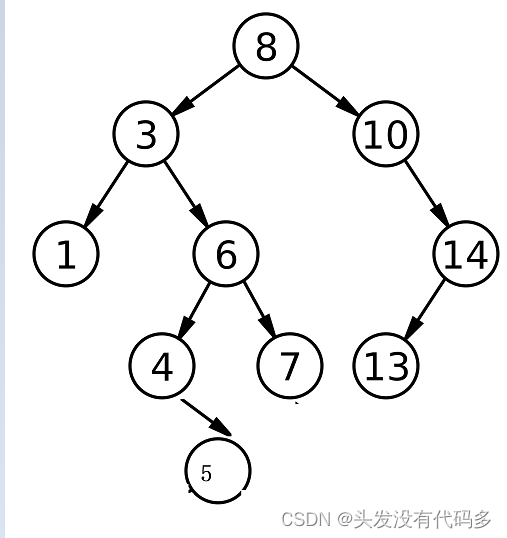
用左子树的最大节1点或右子树的最小节点4，若采用右树的最小节点，交换3和4删除4之后，删除3，但还有一个子节点5，我们让5成为6的左节点

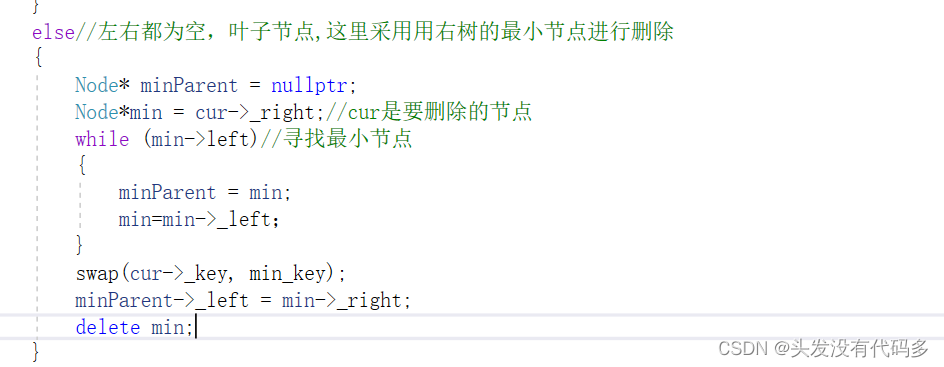
若要删除8，这里采用右树最左节点的替换法，右树的最左节点就是10自己，如果这样写会有错误，while循环都不会进去，minparent就是空，而后面minParent->_left = min->_right;这个语句会出错，修正方法，让minparent一开始就是cur，并且加个判断。

这样写即可

非递归删除代码 

	bool Erase(const K& key)//删除
	{
		//若有一个子节点，删除父节点后，让子节点填充
		//若有俩个子节点，父节点删除后
		//1.用左子树的最大节点替换父节点
		//2.或右子树的最小节点替换父节点
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else//找到了
			{
				if (cur->_left == nullptr)//如果要删除的节点左为空
				{
					if (cur == _root)//如果要删除的是根节点(这种情况根节点只有右子树，因为左为空)
					{
						_root = cur->_right;
					}
					else
					{
						if (cur == parent->_left)//判断要删除的节点是父亲的左节点还是右节点
						{
							parent->_left = cur->_right;
						}
						else
						{
							parent->_right = cur->_right;
						}
					}
					delete cur;
					cur = nullptr;
				}
				else if (cur->_right == nullptr)//如果要删除的节点右为空
				{
					if (cur == _root)
					{
						_root = cur->_left;
					}
					else
					{
						if (cur == parent->_left)//判断要删除的节点是父亲的左节点还是右节点
						{
							parent->_left = cur->_left;
						}
						else
						{
							parent->_right = cur->_left;
						}
					}
					delete cur;
					cur = nullptr;
				}
				else//左右都为空，叶子节点,这里采用用右树的最小节点进行删除
				{
					Node* minParent = cur;
					Node*min = cur->_right;//cur是要删除的节点
					while (min->_left)//寻找最小节点
					{
						minParent = min;
						min = min->_left;
					}
					swap(cur->_key, min->_key);
					if (minParent->_left == min)
					{
						minParent->_left = min->_right;
					}
					else
					minParent->_right = min->_right;
					delete min;
				}
				return true;
			}
		}
		return false;
	}

递归查找 

	bool _FindR(Node *root,const K& key)
	{
		if (root == nullptr)
			return false;
		if (root->_key < key)
		{
			return _FindR(root->right, key);
		}
		else if (root->_key > key)
		{
			return _FindR(root->left, key);
		}
		else
		{
			return true;
		}
	}

 递归插入

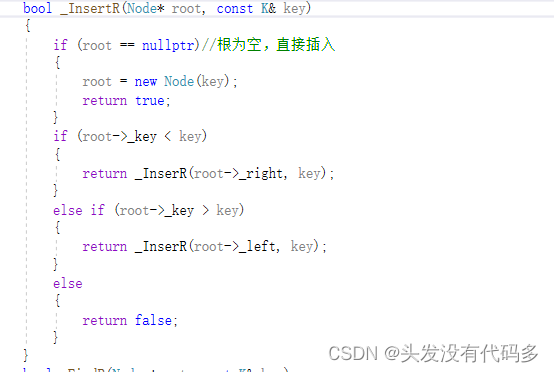
这种插入写法会导致二叉树断开

 这里的Node没有跟父节点连接上，而是创建了一个空间单独在那里

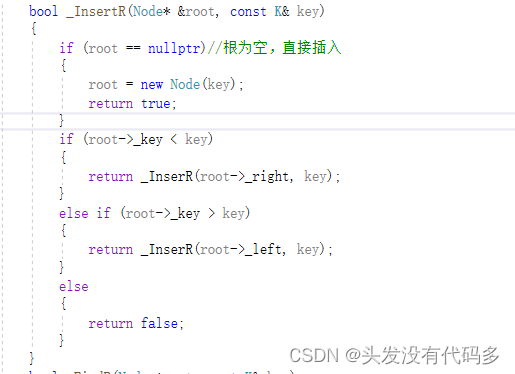
 加上引用即可

	bool _InsertR(Node*& root, const K& key)
	{
		if (root == nullptr)//根为空，直接插入
		{
			root = new Node(key);
			return true;
		}
		if (root->_key < key)
		{
			return _InsertR(root->_right, key);
		}
		else if (root->_key > key)
		{
			return _InsertR(root->_left, key);
		}
		else
		{
			return false;
		}
	}

递归删除 

	bool _Eraser(Node*& root, const K& key)
	{
		if (root == nullptr)
			return false;
		if (root->_key < key)
		{
			return _Eraser(root->_right, key);
		}
		else if (root->_key > key)
		{
			return _Eraser(root->_left, key);
		}
		else
		{
			Node* del = root;
			if (root->_left == nullptr)
			{
				root = root->_right;
			}
			else if (root->_right == nullptr)
			{
				root = root->_left;//由于是引用，可直接这样将二叉树连接起来
			}
			else
			{
				//找右树的最左节点
				Node* min = root->_right;
				while (min->_left)
				{
					min = min->_left;
				}
				swap(root->_key, min->_key);
				return _Eraser(root->_right, key);
			}
			delete del;
			return true;
		}
	}

析构函数 

	~BStree()
	{
Destory(_root);
	}
private:
	void Destory(Node*& root)//采用引用可让root置空起作用
	{
		if (root ==nullptr)
			return;
		Destory(root->_left);
		Destory(root->right);
		delete root;
		root=nullptr
	}

拷贝构造 

 注：拷贝构造也是构造，如果写了构造，编译器不会生成默认构造，会报错没有合适的默认构造

	BStree(const BStree<K> & t)
	{
		_root = _Copy(t._root);
	}
Node* _Copy(Node* root)
	{
		if (root == nullptr)
		{
			return nullptr;
		}
		Node* copyRoot = new Node(root->_key);
		copyRoot->_left = _Copy(root->_left);
		copyRoot->_right = _Copy(root->_right);
		return copyRoot;
	}

我们需加默认构造 

默认构造也可写为BSTree()=default;

这是强制编译器生成默认构造，是C++11的用法

赋值重载

	BStree<K>& operator=(BStree<K> t)
	{
		swap(_root, t._root);
		return *this;
	}

搜索二叉树增删查的时间复杂度是：O（h），h代表高度 

完整代码 

#include<iostream>
using namespace std;
template<class K>
class BStreeNode
{
public:
	BStreeNode(const K& key)
		:_left(nullptr),
		_right(nullptr),
		_key(key)
	{}
	BStreeNode<K>* _left;
	BStreeNode<K>* _right;
	K _key;
};
template<class K>
class BStree
{
	typedef BStreeNode<K> Node;
public:
	bool Insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}

		cur = new Node(key);
		if (parent->_key < key)
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}

		return true;
	}
	void InOrder()//排序
	{
		_InOrder(_root);
	}
	bool Find(const K& key)//查找
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				cur = cur->_left;
			}
			else
			{
				return true;
			}
		}

		return true;
	}
	bool Erase(const K& key)//删除
	{
		//若有一个子节点，删除父节点后，让子节点填充
		//若有俩个子节点，父节点删除后
		//1.用左子树的最大节点替换父节点
		//2.或右子树的最小节点替换父节点
		Node* parent = nullptr;
		Node* cur = _root;

		while (cur)
		{
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else//找到了
			{
				if (cur->_left == nullptr)//如果要删除的节点左为空
				{
					if (cur == _root)//如果要删除的是根节点(这种情况根节点只有右子树，因为左为空)
					{
						_root = cur->_right;
					}
					else
					{
						if (cur == parent->_left)//判断要删除的节点是父亲的左节点还是右节点
						{
							parent->_left = cur->_right;
						}
						else
						{
							parent->_right = cur->_right;
						}
					}
					delete cur;
					cur = nullptr;
				}
				else if (cur->_right == nullptr)//如果要删除的节点右为空
				{
					if (cur == _root)
					{
						_root = cur->_left;
					}
					else
					{
						if (cur == parent->_left)//判断要删除的节点是父亲的左节点还是右节点
						{
							parent->_left = cur->_left;
						}
						else
						{
							parent->_right = cur->_left;
						}
					}
					delete cur;
					cur = nullptr;
				}
				else//左右都为空，叶子节点,这里采用用右树的最小节点进行删除
				{
					Node* minParent = cur;
					Node* min = cur->_right;//cur是要删除的节点
					while (min->_left)//寻找最小节点
					{
						minParent = min;
						min = min->_left;
					}
					swap(cur->_key, min->_key);
					if (minParent->_left == min)
					{
						minParent->_left = min->_right;
					}
					else
						minParent->_right = min->_right;
					delete min;
				}
				return true;
			}
		}
		return false;
	}
	bool FindR(const K& key)
	{
		return _FindR(_root, key);
	}
	bool InsertR(const K& key)
	{
		return _InsertR(_root, key);
	}
	bool EraseR(const K& key)
	{
		return _Eraser(_root, key);
	}
	~BStree()
	{
		Destory(_root);
	}
	BStree()
	{}
	BStree(const BStree<K>& t)
	{
		_root = _Copy(t._root);
	}
	BStree<K>& operator=(BStree<K> t)
	{
		swap(_root, t._root);
		return *this;
	}
private:
	Node* _Copy(Node* root)
	{
		if (root == nullptr)
		{
			return nullptr;
		}
		Node* copyRoot = new Node(root->_key);
		copyRoot->_left = _Copy(root->_left);
		copyRoot->_right = _Copy(root->_right);
		return copyRoot;
	}
	void Destory(Node*& root)//采用引用可让root置空起作用
	{
		if (root == nullptr)
			return;
		Destory(root->_left);
		Destory(root->_right);
		delete root;
		root = nullptr;
	}
	bool _Eraser(Node*& root, const K& key)
	{
		if (root == nullptr)
			return false;
		if (root->_key < key)
		{
			return _Eraser(root->_right, key);
		}
		else if (root->_key > key)
		{
			return _Eraser(root->_left, key);
		}
		else
		{
			Node* del = root;
			if (root->_left == nullptr)
			{
				root = root->_right;
			}
			else if (root->_right == nullptr)
			{
				root = root->_left;//由于是引用，可直接这样将二叉树连接起来
			}
			else
			{
				//找右树的最左节点
				Node* min = root->_right;
				while (min->_left)
				{
					min = min->_left;
				}
				swap(root->_key, min->_key);
				return _Eraser(root->_right, key);
			}
			delete del;
			return true;
		}
	}
	bool _InsertR(Node*& root, const K& key)
	{
		if (root == nullptr)//根为空，直接插入
		{
			root = new Node(key);
			return true;
		}
		if (root->_key < key)
		{
			return _InsertR(root->_right, key);
		}
		else if (root->_key > key)
		{
			return _InsertR(root->_left, key);
		}
		else
		{
			return false;
		}
	}
	bool _FindR(Node *root,const K& key)
	{
		if (root == nullptr)
			return false;
		if (root->_key < key)
		{
			return _FindR(root->right, key);
		}
		else if (root->_key > key)
		{
			return _FindR(root->left, key);
		}
		else
		{
			return true;
		}
	}
	void _InOrder(Node *root)
	{
		if (root == nullptr)
			return;
		_InOrder(root->_left);
		cout << root->_key << " ";
		_InOrder(root->_right);
	}
private:
	Node* _root = nullptr;
};
int main()
{
	BStree<int> t;
	int a[] = { 1,1,2,2,3,6,165,132,4185,123 };
	for (auto e : a)
	{
		t.Insert(e);
	}
	BStree<int> copy = t;
	copy.InOrder();
	t.InOrder();
	BStree<int> t1;
	t1.Insert(2);
	t1.Insert(1);
	t1.Insert(3);
	copy = t1;
	copy.InOrder();
	cout << endl;
	t1.InOrder();
	cout << endl;
	return 0;
}

 二叉搜索树的应用

 .K模型：K模型即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到
的值。
比如：给一个单词word，判断该单词是否拼写正确，具体方式如下：
以词库中所有单词集合中的每个单词作为key，构建一棵二叉搜索树

在二叉搜索树中检索该单词是否存在，存在则拼写正确，不存在则拼写错误

KV模型：每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。该种方
式在现实生活中非常常见：
比如英汉词典就是英文与中文的对应关系，通过英文可以快速找到与其对应的中文，英
文单词与其对应的中文<word, chinese>就构成一种键值对；


再比如统计单词次数，统计成功后，给定单词就可快速找到其出现的次数，单词与其出
现次数就是<word, count>就构成一种键值对
KV模型通过K去找V

Key/Value模型 

namespace KeyValue
{
	template<class K, class V>
	struct BSTreeNode
	{
		BSTreeNode<K, V>* _left;//Key和Value绑到一起
		BSTreeNode<K, V>* _right;
		K _key;
		V _value;

		BSTreeNode(const K& key, const V& value)
			:_left(nullptr)
			, _right(nullptr)
			, _key(key)
			, _value(value)
		{}
	};

	template<class K, class V>
	class BSTree
	{
		typedef BSTreeNode<K, V> Node;
	public:
		bool Insert(const K& key, const V& value)
		{
			if (_root == nullptr)
			{
				_root = new Node(key, value);
				return true;
			}

			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					return false;
				}
			}

			cur = new Node(key, value);
			if (parent->_key < key)
			{
				parent->_right = cur;
			}
			else
			{
				parent->_left = cur;
			}

			return true;
		}

		Node* Find(const K& key)//查找的时候以K去查找，返回的时候返回节点指针，以便于修改
		{
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key < key)
				{
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					cur = cur->_left;
				}
				else
				{
					return cur;
				}
			}

			return nullptr;
		}

		bool Erase(const K& key)//用K删除
		{
			//...

			return true;
		}

		void InOrder()
		{
			_InOrder(_root);
			cout << endl;
		}
	private:

		void _InOrder(Node* root)
		{
			if (root == nullptr)
			{
				return;
			}

			_InOrder(root->_left);
			cout << root->_key << ":" << root->_value << endl;
			_InOrder(root->_right);
		}
	private:
		Node* _root = nullptr;
	};

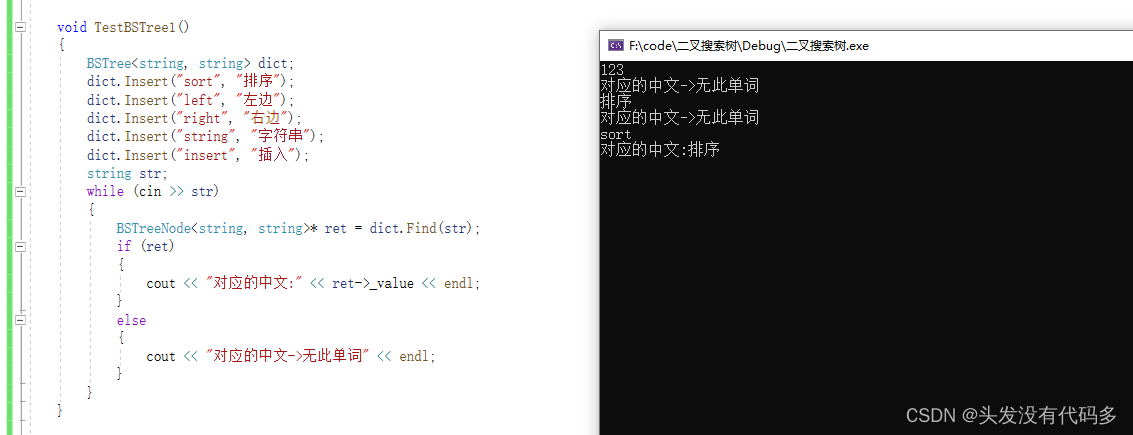
英译汉

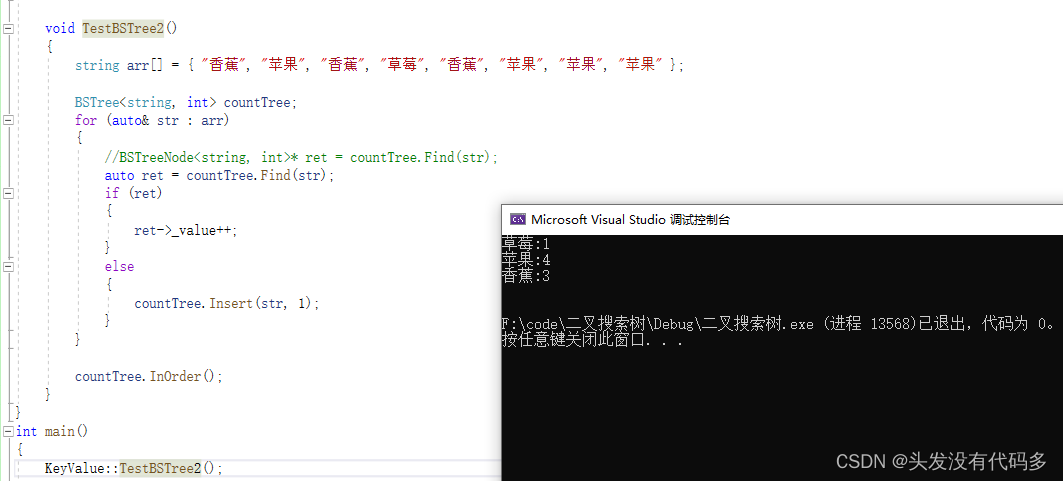
 统计水果出现的次数

 链表相交和复杂链表的赋值可用kv模型。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/49060.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

第3部分 静态路由

第3部分 静态路由

目录 3.1 静态路由与默认路由 3.1.1 静态路由介绍 3.1.2 默认路由介绍 3.2 静态路由命令汇总 转发数据包是路由器的最主要功能。路由器转发数据包时需要查找路由表&#xff0c;管理员可以通过手工的方法在路由器中直接配置路由表&#xff0c;这就是静态路由。虽然静态路由不…
阅读更多...
Dialog的IDE搭建systermView的方法步骤（DA1469X）

Dialog的IDE搭建systermView的方法步骤（DA1469X）

1.背景 SystemView 是一个可以在线调试嵌入式系统的工具&#xff0c;它可以分析有哪些中断、任务执行了&#xff0c;以及这些中断、任务执行的先后关系。还可以查看一些内核对象持有和释放的时间点&#xff0c;比如信号量、互斥量、事件、消息队列等。这在开发和处理具有多个线…
阅读更多...
大规模 MIMO 检测的近似消息传递 （AMP）附Matlab代码

大规模 MIMO 检测的近似消息传递 （AMP）附Matlab代码

✅作者简介&#xff1a;热爱科研的Matlab仿真开发者&#xff0c;修心和技术同步精进&#xff0c;matlab项目合作可私信。 &#x1f34e;个人主页&#xff1a;Matlab科研工作室 &#x1f34a;个人信条&#xff1a;格物致知。 更多Matlab仿真内容点击&#x1f447; 智能优化算法 …
阅读更多...
神经架构搜索的综合调查：挑战和解决方案(一)

神经架构搜索的综合调查：挑战和解决方案(一)

神经架构搜索的综合调查&#xff1a;挑战和解决方案 paper题目&#xff1a;A Comprehensive Survey of Neural Architecture Search: Challenges and Solutions paper是西北大学发表在ACM Computing Surveys 2021的工作 paper地址&#xff1a;链接 ABSTRACT 深度学习以其强大的…
阅读更多...
c#机器学习之opencv（2）-Mat基础

c#机器学习之opencv（2）-Mat基础

目录Mat基础Mat本质copyTo与cloneMat基础 opencv将图像数据存在一个二维矩阵里。 下面代码复制了一个图像矩阵。 Mat srcPic new Mat("test1.png", ImreadModes.Color); Mat aPic new Mat(srcPic,new OpenCvSharp.Rect(100,120, srcPic.Width-100, srcPic.Heigh…
阅读更多...
1.8 打好shell基础

1.8 打好shell基础

一、常用shell命令 1、管道命令 &#xff08;1&#xff09;命令格式 &#xff08;2&#xff09;案例演示 任务1、查看/etc目录信息前5行信息 执行命令&#xff1a;ll /etc | head -5 任务2、查看/etc/profile文件后5行信息 执行命令&#xff1a;cat /etc/profile | tai…
阅读更多...
大数据培训FileInputFormat实现类

大数据培训FileInputFormat实现类

FileInputFormat实现类 思考:在运行MapReduce程序时&#xff0c;输入的文件格式包括:基于行的日志文件、 二进制格式文件、数据库表等。那么&#xff0c;针对不同的数据类型&#xff0c;MapReduce是如 何读取这些劣如据的呢? FileInputFormat常见的接口实现类包括:TextInputF…
阅读更多...
mapreduce搭建

mapreduce搭建

一.虚拟机安装CentOS7并配置共享文件夹 二.CentOS 7 上hadoop伪分布式搭建全流程完整教程 三.本机使用python操作hdfs搭建及常见问题 四.mapreduce搭建 五.mapper-reducer编程搭建 mapreduce搭建一、配置1.创建mapred-site.xml文件2.编辑mapred-site.xml二、打开hadoop0.删除da…
阅读更多...
virtio-net 实现机制【一】（图文并茂）

virtio-net 实现机制【一】（图文并茂）

1. 基于virtio的半虚拟化概述 1.1 virtio运行结构 ① virtio表示虚拟化IO&#xff0c;用于实现设备半虚拟化&#xff0c;即虚拟机中运行的操作系统需要加载特殊的驱动&#xff08;e.g. virtio-net&#xff09;且虚拟机知道自己是虚拟机 相较于基于完全模拟的全虚拟化&#xf…
阅读更多...
PR-视频加介绍背景

PR-视频加介绍背景

每天一个PS/PR小技巧&#xff08;原理实践&#xff09; 比如我们有一个展示视频&#xff0c;我们希望在视频一开始时添加一个介绍背景&#xff08;纯色背景&#xff09;&#xff1a; 点击新建->颜色遮罩&#xff1a; 定义名称&#xff0c;选择颜色&#xff0c;然后就能在工…
阅读更多...
Bug: conda环境与jupyter notebook kernel核环境不一致

Bug: conda环境与jupyter notebook kernel核环境不一致

问题 一般在服务器上进行环境安装的时候有多种方式&#xff0c;比如docker, conda等。conda肯使用起来更加简便&#xff0c;docker更适合服务器部署的时候使用。 本文记录在使用conda时候出现的问题&#xff0c;jupter notebook中的环境不一致导致的。 首先conda创建环境 co…
阅读更多...
蓝桥杯嵌入式第二篇配置按键

蓝桥杯嵌入式第二篇配置按键

文章目录前言一、原理图查看二、cubeMX配置三、代码讲解(使用按键控制LED灯的开关)四、HAL_Delay的内部实现五.遗留的问题总结前言 点完灯后接下来我们就开始按键的学习了&#xff0c;这也是很简单的&#xff0c;大家不用担心。 一、原理图查看 可以看到板子上面是有4个按键…
阅读更多...
定时任务多线程-springboot

定时任务多线程-springboot

定时任务 在项目开发过程中&#xff0c;经常需要定时任务来帮助我们实现某些业务功能&#xff0c;比如定时生成数据报表、生成对账单、订单超时处理等。Spring Boot提供了内置的Scheduled注解实现定时任务的功能。 步骤 1.修改启动类 在启动类上加上EnableScheduling开启定时…
阅读更多...
华为数字化转型之道 方法篇 第五章 视IT为投资，用产品思维管理IT

华为数字化转型之道 方法篇 第五章 视IT为投资，用产品思维管理IT

第五章 视IT为投资，用产品思维管理IT 5.1 数字时代IT系统的重新定位 比较传统信息化和数字化转型下的IT系统特征，我们发现业务环境、IT能力、业务和IT的关系都发生了巨大的变化（见图5-1） 从“管理系统”到“作业平台” 传统信息化下的IT系统往往侧重于信息记录、流程固化…
阅读更多...
LeetCode994. 腐烂的橘子(C++中等题)

LeetCode994. 腐烂的橘子(C++中等题)

题目 在给定的 m x n 网格 grid 中&#xff0c;每个单元格可以有以下三个值之一&#xff1a; 值 0 代表空单元格&#xff1b; 值 1 代表新鲜橘子&#xff1b; 值 2 代表腐烂的橘子。 每分钟&#xff0c;腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。 返回 直到单元格…
阅读更多...
因子模型：协方差矩阵

因子模型：协方差矩阵

本文是Quantitative Methods and Analysis: Pairs Trading此书的读书笔记。 因子协方差矩阵&#xff08;factor covariance matrix&#xff09;在计算风险的时候很重要。如果一个模型有个因子&#xff0c;那么协方差矩阵的大小就是。对角线元素是每个因子的方差&#xff0c;非…
阅读更多...
[附源码]Python计算机毕业设计SSM流浪动物管理系统（程序+LW)

[附源码]Python计算机毕业设计SSM流浪动物管理系统（程序+LW)

项目运行 环境配置&#xff1a; Jdk1.8 Tomcat7.0 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; SSM mybatis Maven Vue 等等组成&#xff0c;B/S模式 M…
阅读更多...
用Python来开发安卓程序：(1)BeeWare安卓开发环境的搭建

用Python来开发安卓程序：(1)BeeWare安卓开发环境的搭建

文章目录1. 前言2. BeeWare简介3. 开发环境搭建注意事项4. 安装BeeWare5. 开发环境搭建5.1 创建项目5.1.1 创建一个新项目5.2 运行项目5.3 打包项目5.3.1 打包为Windows程序5.3.1.1 首先briefcase create安装应用的脚手架5.3.1.2 然后构建应用5.3.1.3 接着&#xff0c;运行构建…
阅读更多...
2. JVM内存模型

2. JVM内存模型

1. JVM虚拟机内存模型图解 JAVA虚拟机主要由这三部分组成类装载子系统&#xff0c;字节码执行引擎&#xff0c;运行时数据区上一节我们不是学了类的加载吗&#xff0c;那些类加载器许多都是C帮我们做的&#xff0c;那么我们这个类装载子系统就是帮我们把类放入运行时数据区的&a…
阅读更多...
[附源码]Python计算机毕业设计SSM浪漫烘焙屋（程序+LW)

[附源码]Python计算机毕业设计SSM浪漫烘焙屋（程序+LW)

项目运行 环境配置&#xff1a; Jdk1.8 Tomcat7.0 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; SSM mybatis Maven Vue 等等组成&#xff0c;B/S模式 M…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023