本文是Quantitative Methods and Analysis: Pairs Trading此书的读书笔记。
因子协方差矩阵(factor covariance matrix)在计算风险的时候很重要。如果一个模型有个因子,那么协方差矩阵的大小就是
。对角线元素是每个因子的方差,非对角线元素是协方差,这些协方差有可能不为零。
协方差矩阵是对称的。
协方差矩阵是正定的。正定的意思是,对于协方差矩阵,存在矩阵
,使得
。
现在考虑一个情况,我们需要估计两个股票A和B回报的协方差。用和
分别表示两个股票的因子暴露系数(factor exposure)向量。那么它们的协方差表示为:
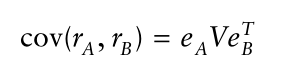
如果有5000个股票,那么协方差矩阵就是一个5000*5000的矩阵了。计算每一个股票的方差以及每一对股票的协方差计算量会很大。对于所有股票的回报的协方差矩阵表示为:

X是因子暴露系数矩阵,V是因子协方差矩阵。
协方差矩阵也是从历史数据中计算出来的,所以存在一些问题,比如过拟合。还有一个问题,对于计算的方差假定它们是服从高斯分布的,而这个假设可能不符合现实中金融时间序列的回报的方差肥尾现象的广泛存在。(肥尾指这样一类事件:它们在突然变本加厉袭来之前看似发生几率极低、通常不被人们重视)。
看一个计算两个股票回报的协方差的例子:

![[附源码]Python计算机毕业设计SSM流浪动物管理系统(程序+LW)](https://img-blog.csdnimg.cn/68e663b1e61c4014a0742ddb2c392f53.png)

![[附源码]Python计算机毕业设计SSM浪漫烘焙屋(程序+LW)](https://img-blog.csdnimg.cn/eed66e8b4d9242ed9fcc69d3bed281d4.png)
![[附源码]Python计算机毕业设计Django的桌游信息管理系统](https://img-blog.csdnimg.cn/df73f78571b64ffb93e5bae450d041ba.png)