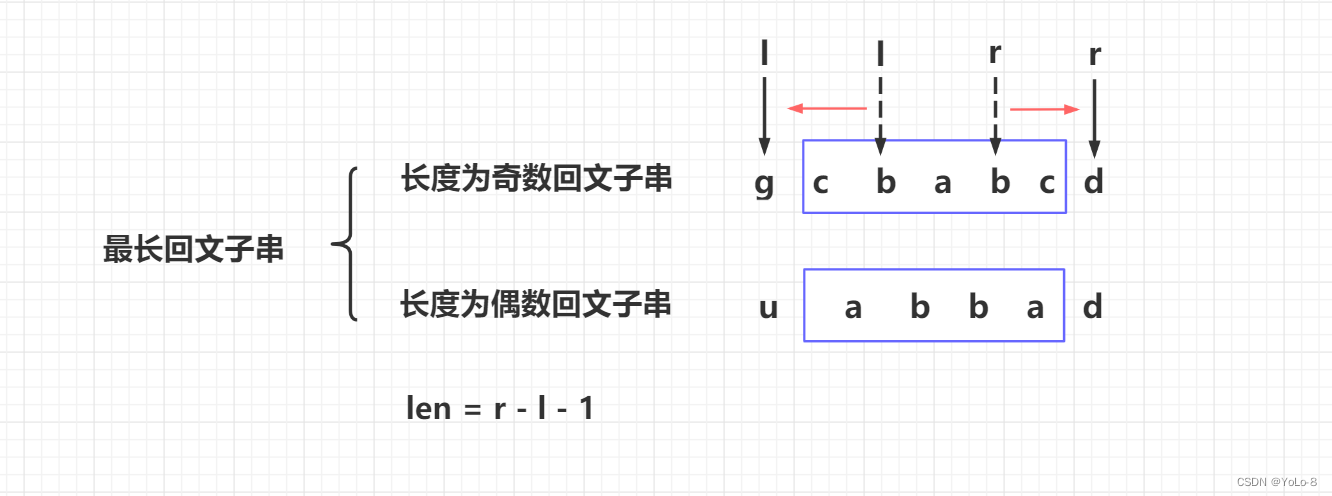
大津算法是一种自适应图像二值化方法。
它以最大化类内距离或最小化类间距离为优化目标,将图像从某一亮度阈值分为前景/背景。
其基本原理示意图如下:

1.前言
为了深入介绍此算法,先说明一些背景知识。
1.1 数据可分性
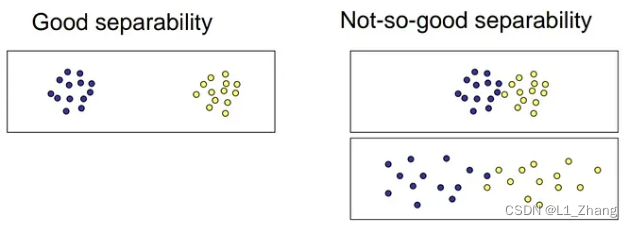
数据可分性通常使用类间及类内距离来评判,即类间距离越大,类内距离越小,数据越容易进行分类/聚类。
1.1 类间方差、类内方差及全局方差
设一数据集 { x i ; i = 1 , 2 , . . . , N } \{x_i;i=1,2,...,N\} {xi;i=1,2,...,N},将其分为 c c c 类,第 j j j 类个数为 n j n_j nj,记为:
{ x i j ; j = 1 , 2 , . . . , c , i = 1 , 2 , . . . , n j } \qquad\qquad\qquad {\{x_i^j;j=1,2,...,c,i=1,2,...,n_j\}} {xij;j=1,2,...,c,i=1,2,...,nj}。
-
所有数据均值 m = 1 N ∑ i = 1 N x i \qquad m=\cfrac{1}{N}\sum\limits_{i=1}^Nx_i m=N1i=1∑Nxi
-
第 j j j 类数据均值 m j = 1 n j ∑ i = 1 n j x i \quad m_j=\cfrac{1}{n_j}\sum\limits_{i=1}^{n_j}x_i mj=nj1i=1∑njxi
-
类内方差
S W j = 1 n j ∑ i = 1 n j ( x i j − m j ) ( x i j − m j ) T \qquad\qquad\qquad\quad S_W^j=\cfrac{1}{n_j}\sum\limits_{i=1}^{n_j}(x_i^j-m_j)(x_i^j-m_j)^T SWj=nj1i=1∑nj(xij−mj)(xij−mj)T -
总的类内方差
S W = ∑ i = 1 c n j N ⋅ S W j \qquad\qquad\qquad\quad S_W=\sum\limits_{i=1}^{c}\cfrac{n_j}{N}\cdot S_W^j SW=i=1∑cNnj⋅SWj -
类间方差
S B = ∑ j = 1 c n j N ( m j − m ) ( m j − m ) T \qquad\qquad\qquad\quad S_B=\sum\limits_{j=1}^{c}\cfrac{n_j}{N}(m_j-m)(m_j-m)^T SB=j=1∑cNnj(mj−m)(mj−m)T -
全局方差
S T = 1 N ∑ i = 1 N ( x j − m ) ( x j − m ) T \qquad\qquad\qquad\quad S_T=\cfrac{1}{N}\sum\limits_{i=1}^{N}(x_j-m)(x_j-m)^T ST=N1i=1∑N(xj−m)(xj−m)T可见,对于同一组数据,其全局方差为一常数。
1.2 三种方差之间的关系
S T = S W + S B \qquad\qquad\qquad\quad S_T=S_W+S_B ST=SW+SB
证明见参考文献[2]。
1.3 评判数据可分性metric
其中一种方法是Calinski-Harabasz Index。
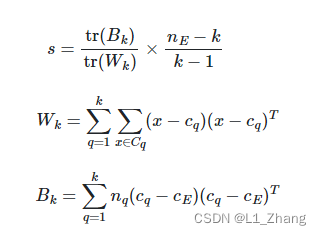
B
k
B_k
Bk,
W
k
W_k
Wk即1.1中的
S
B
S_B
SB,
S
W
S_W
SW。
sklearn中有相应的实现:
from sklearn import metrics
metrics.calinski_harabasz_score(X, labels)
2. OSTU算法
从1.2可知,对于同一组数据,全局方差为一常数,则最大化类间方差等价于最小化类内方差。
因此对于图像二值化,优化目标可设为最大化前景/背景两类之间的方差。
这里直接列出 wiki Otsu中的方法:



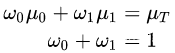
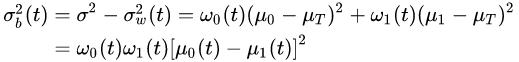
- 具体算法:
1) 计算图像直方图,统计每一个亮度水平 i = 0 , 1 , . . . , L i=0,1,...,L i=0,1,...,L 的比例 p i p_i pi;
2) for t = 1 , . . . , L t=1,...,L t=1,...,L,分别计算类间方差 σ b 2 ( t ) \sigma_b^2(t) σb2(t);
3)二值化亮度阈值设为 最大 σ b 2 ( t ) \sigma_b^2(t) σb2(t)对应的t值。
参考文献
[1] Otsu Thresholding — Mathematical Secrets behind Image Binarization
[2] 现代模式识别,孙即祥
[3] https://scikit-learn.org/stable/modules/clustering.html#calinski-harabasz-index
[4] wiki Otsu