1、构造二叉树

树节点：

// 二叉树节点的构造函数
function TreeNode(val, left, right) {
    this.val = (val===undefined ? 0 : val)
    this.left = (left===undefined ? null : left)
    this.right = (right===undefined ? null : right)
}

下面我们需要遍历下面这颗二叉树：

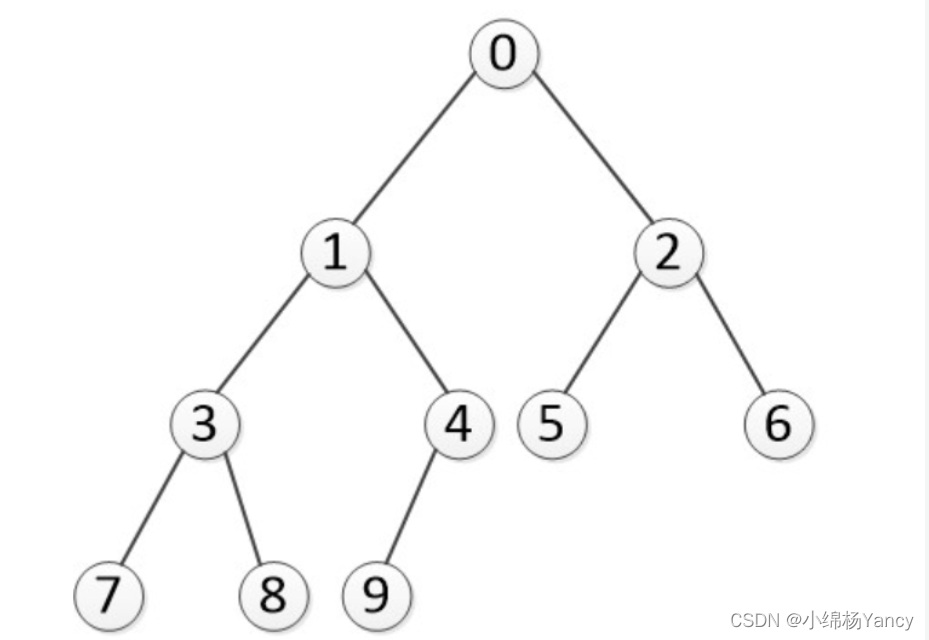
遍历结果：
先序：“中 - 左 - 右” 0137849256
中序：“左 - 中 - 右” 7381940526
后序：“左 - 右 - 中” 7839415620

2、递归遍历

调用递归的位置不同，结果分为三种。

var preorder = []// 前序结果
var inorder = []// 中序结果
var postorder = []// 后序结果

var loop = function(root){
	// 当前节点为空，表示达到了叶子节点
    if (root == null) return

    preorder.push(root.val)  // 前序
    loop(root.left)
    inorder.push(root.val)// 中序
    loop(root.right)
    postorder.push(root.val)// 后序
}
loop(root)

3、非递归遍历

3.1 先序

1. 根节点入栈，依此取出栈顶元素。
2. 访问栈顶元素，同时出栈，将栈顶元素作为当前元素，当前元素右节点入栈，左节点入栈（注意：右先入那么右后出）。
3. 重复上述操作，直到整个栈为空时，则遍历结束。

var preorderTraversal = function(root) {
    var arr = []
    arr.push(root)
    var res = []
    while (arr.length) {
        var temp = arr.pop()
        if (!temp) break;
        //当前节点的值放入结果数组
        res.push(temp.val)
        //右子树入栈
        if (temp.right) {
            arr.push(temp.right)
        }
        //左子树入栈
        if (temp.left) {
            arr.push(temp.left)
        }
    }
    return res
};

3.2 中序

1. 循环将根节点和其的左子树入栈。
2. 直到左子树为空时，访问栈顶元素，同时将栈顶元素作为当前元素，并出栈。
3. 开始访问右子树，循环出栈直到整个栈为空时，则遍历结束。

var inorderTraversal = function(root) {
    var res = []
    var arr = []

    while(arr.length || root) {
        if (root) {
            arr.push(root)
            root = root.left
        } else {
            let temp = arr.pop()
            res.push(temp.val)
            root = temp.right
        }
    }

    return res
};

3.3 后序

和前序遍历思想相反。
先序是使用push往res数组后面加数据，二后序是使用unshift往数组前面加数据。

var postorderTraversal = function(root) {
    var arr = []
    arr.push(root)
    var res = []
    while(arr.length) {
        var temp = arr.pop()
        if (!temp) break
        res.unshift(temp.val)// 从前往后塞入数据
        if(temp.left) {// 左节点先入栈
            arr.push(temp.left)
        }
        if(temp.right) {
            arr.push(temp.right)
        }
    }

    return res
};