一、问题

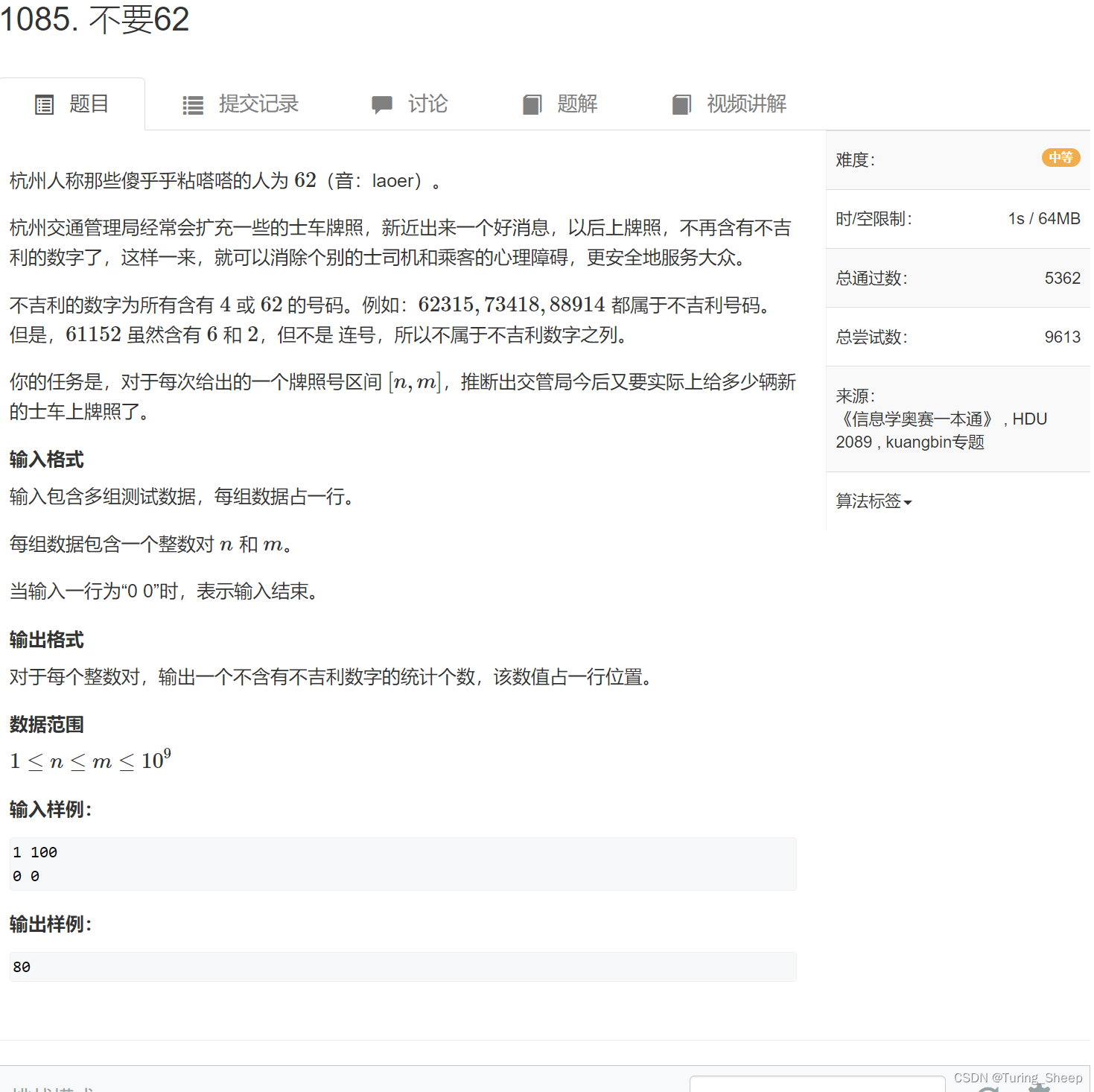
二、分析

这道题涉及的算法是数位DP。如果大家不懂数位DP的话，可以先去看作者之前的文章：第五十章 动态规划——数位DP模型

假设一个数$n$，我们先求出从$1$到$n$当中，所有不含数字4和62的数字的个数。我们将这个过程封装为一个函数，先来分析一下这个函数怎么写。

按照数位DP的分析逻辑，先将$n$的每一位存储在$vector$中，然后从高位开始枚举。

对于其中的任意一位$a$。由于我们求的是从$1$到$n$的数字，所以在该位之前所有高位都相同的条件下，该位所填的数字必须是$\le a$的，这样做才能小于等于$n$。

我们现在分成两类，一类是该位$<a$。
在这种情况下，我们就无需考虑数字大小的问题了，因为该位小于$a$，所以比该位小的位可以随便写，无论怎么写都是小于$a$的。那么我们又怎么统计该情况下，符合题目要求的数字个数呢？

求个数的过程就是我们真正需要写DP的部分。这里我们先直接利用DP的状态定义解决这个函数，具体的状态转移我们后面再说。
我们让状态：$f[i][k]$表示数字有$i$位，并且第$i$位是$k$的情况下， 数字中不含$4$、$62$的数字个数。那么我们这里直接将$k$从$0$到$a-1$进行枚举$f[i][k]$，然后将这些累加到结果上。但并不是所有都能累加的，比如$k=4$的时候，就不可以。再比如上一位的数字和当前位的$k$组成$62$的时候，也是不能算的。（这就说明我们还需要一个$last$变量去存储上一位的数字。）

当这一位是$a$的时候，我们只需要接着往后讨论，但是如果第$a$位是$4$的话，说明无论后面是什么，组成的数字都是不符合题目要求的，直接挑出循环即可。

接下来，我们分析一下状态转移应该怎么写？

$$Af[i][k]+=f[i-1][j]$$
上面的$j$是从$0$到$9$的。但是要注意的是，$j$和$k$不能是$4$，并且$j$和$k$不能组成$62$。

三、代码

#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 35;

int f[N][10];

void init()
{
    for (int i = 0; i <= 9; i ++ )
        if (i != 4)
            f[1][i] = 1;

    for (int i = 1; i < N; i ++ )
        for (int j = 0; j <= 9; j ++ )
        {
            if (j == 4) continue;
            for (int k = 0; k <= 9; k ++ )
            {
                if (k == 4 || j == 6 && k == 2) continue;
                f[i][j] += f[i - 1][k];
            }
        }
}
int dp(int n)
{
    if (!n) return 1;

    vector<int> nums;
    while (n) nums.push_back(n % 10), n /= 10;

    int res = 0;
    int last = 0;
    for (int i = nums.size() - 1; i >= 0; i -- )
    {
        int x = nums[i];
        for (int j = 0; j < x; j ++ )
        {
            if (j == 4 || last == 6 && j == 2) continue;
            res += f[i + 1][j];
        }

        if (x == 4 || last == 6 && x == 2) break;
        last = x;

        if (!i) res ++ ;
    }

    return res;
}
int main()
{
    init();

    int l, r;
    while (cin >> l >> r, l || r)
    {
        cout << dp(r) - dp(l - 1) << endl;
    }

    return 0;
}