参考博客:快速排序算法详解(原理、实现和时间复杂度)
排序算法的思想非常简单,在待排序的数列中,我们首先要找一个数字作为基准数(这只是个专用名词)。为了方便,我们一般选择第 1 个数字作为基准数(其实选择第几个并没有关系)。接下来我们需要把这个待排序的数列中小于基准数的元素移动到待排序的数列的左边,把大于基准数的元素移动到待排序的数列的右边。这时,左右两个分区的元素就相对有序了;接着把两个分区的元素分别按照上面两种方法继续对每个分区找出基准数,然后移动,直到各个分区只有一个数时为止。
这是典型的分治思想,即分治法。下面我们对一个实际例子进行算法描述,讲解快速排序的排序步骤。
以 47、29、71、99、78、19、24、47 的待排序的数列为例进行排序,为了方便区分两个 47,我们对后面的 47 增加一个下画线,即待排序的数列为 47、29、71、99、78、19、24、47。
首先我们需要在数列中选择一个基准数,我们一般会选择中间的一个数或者头尾的数,这里直接选择第 1 个数 47 作为基准数,接着把比 47 小的数字移动到左边,把比 47 大的数字移动到右边,对于相等的数字不做移动。所以实际上我们需要找到中间的某个位置 k,这样 k 左边的值全部比 k 上的值小,k 右边的值全部比 k 上的值大。
接下来开始移动元素。怎么移动呢?其实冒泡排序也涉及对元素的移动,但是那样移动起来很累,比如把最后一个元素移动到第 1 个,就需要比较 n-1 次,同时交换 n-1 次,效率很低。其实,只需把第 1 个元素和最后一个元素交换就好了,这种思想是不是在排序时可以借鉴呢?之前说快速排序就是对冒泡排序的一个改进,就是这个原因。
快速排序的操作是这样的:首先从数列的右边开始往左边找,我们设这个下标为 i,也就是进行减减操作(i--),找到第 1 个比基准数小的值,让它与基准值交换;接着从左边开始往右边找,设这个下标为 j,然后执行加加操作(j++),找到第 1 个比基准数大的值,让它与基准值交换;然后继续寻找,直到 i 与 j 相遇时结束,最后基准值所在的位置即 k 的位置,也就是说 k 左边的值均比 k 上的值小,而 k 右边的值都比 k 上的值大。
所以对于上面的数列 47、29、71、99、78、19、24、47,进行第 1 趟第 1 个交换的排序情况如下,第 1 次的操作情况如图 1 所示。
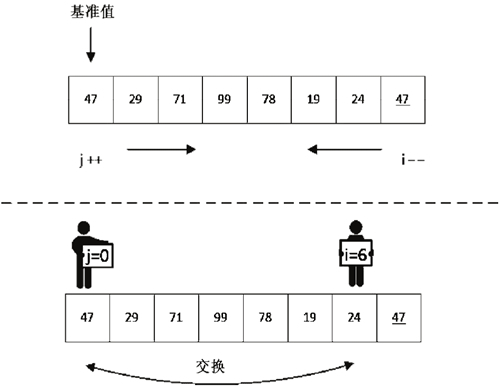
图 1 第 1 次发现可以交换的数
交换之后,j 移动到了下标为 6 的位置,对 i 继续扫描,如图 2 所示。

图 2 第 2 次发现可交换的值
此时交换后的数列变为 24、29、47、99、78、19、71、47。接下来我们继续对 i、j 进行操作,如图 3 所示,继续进行 i-- 及 j++ 的比较操作。
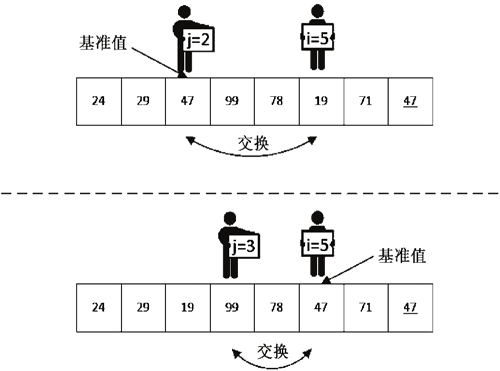
图 3 继续进行 i 与 j 的移动
进行了这两次 i、j 的移动、比较、交换之后,我们最终得到的数列是 24、29、19、47、78、99、71、47。接下来我们继续进行 i-- 的操作,发现在 i 为 4 时比 47 大不用交换,在 i 为 3 时与 j 相遇,这时就不需要继续移动、比较了,已经找到 k 了,并且 k 的值为 3。我们可以确认一下当前的数列是不是 k 左边的值都比 47 小,而 k 右边的值都比 47 大(由于要保持相对位置不变,所以 47 同样在基准值 47 的右边)。
47 这个值已经落到了它该在的位置,第 1 趟排序完成了。接下来就是以 k 为基准,分为两部分,然后在左右两部分分别执行上述排序操作,最后数据会分为 4 部分;接着对每部分进行操作,直到每部分都只有一个值为止。
接下来进行第 2 趟排序,现在左边部分为 24、29、19,我们选择第 1 个数 24 作为基准数,接着进行 i--、j++ 的操作,我们发现 i 最初的值为 19,比 24 这个基准值小,所以与基准值进行交换,得到的数列为 19、29、24;当 j 为 1 时,我们发现 29 比 24 大,所以与基准值进行交换,得到的数列 19、24、29,此时 i 为 2,j 为 1;继续 i-- 时发现 i 为 1,与 j 相遇,左边部分的数列的 k 为 1,并且左右两部分分别只有一个元素,此时第 2 轮排序的左边部分的排序结束,同时左边部分的所有数据都排序完成。
我们接着看右边部分的排序,待排序的数列为 78、99、71、47,我们同样选择第 1 个值 78 为基准值,接下来进行 i 与 j 的移动与比较,发现 47 比 78 小,进行交换,得到的数列 47、99、71、78;从左往右发现 99 比基准值 78 大,进行交换,得到的数列为 47、78、71、99;继续从右向左看,发现 71 比基准值 78 小,进行交换,得到的数列为 47、71、78、99。此时 i 在整体数组中的下标为 6,j 为 5,若继续 j++ 则与 i 相遇,所以完成此轮排序。
此时右边数列的 k 为 6,一般会是相遇的位置,也就是基准值所在的位置,这时数列又被分为两部分,左边是 47、71,右边是 99,需要继续对左边部分的数据进行排序,虽然只有两个数据,但我们还是继续按照快速排序的思想操作一下,选择 47 作为基准数,将i进行从右向左的移动、比较,发现 i 与 j 相等时没有产生移动,完成第 2 轮排序。
至此,所有排序都已经完成,最终数列的结果是 19、24、29、47、47、71、78、99,怎么样,快速排序是不是非常简单地完成了所有的排序呢?虽然本次快速排序没有改变相同值的元素的顺序,但是由于快速排序需要对数列中的元素来回移动,有时还是会改变相对顺序的(比如 47 在第 1 轮的移动过程中就被移动到 47 的右边了),所以快速排序并不是一个稳定的算法。
快速排序的实现
通过以上的学习,你是否可以自己写出快速排序的实现代码呢?在接着学习之前,最好自己能对代码的实现进行一些思考,然后和下面的内容进行比对,看看自己有哪些疏忽之处。
其实快速排序有一个比较简单的思想,就是递归。对于每一趟排序都是一样的思想,只不过需要进行排序的数组的范围越来越小了,使用递归实现这种排序最适合不过了。
给定一个长度为 n 的可能有重复值的数组,找出其中不去重的最小的 k 个数。例如数组元素是4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4(任意顺序皆可)。
数据范围:0≤�,�≤100000≤k,n≤10000,数组中每个数的大小0≤���≤10000≤val≤1000
要求:空间复杂度 �(�)O(n) ,时间复杂度 �(�����)O(nlogk)
示例1
输入:
[4,5,1,6,2,7,3,8],4
复制返回值:
[1,2,3,4]
复制说明:
返回最小的4个数即可,返回[1,3,2,4]也可以
示例2
输入:
[1],0
复制返回值:
[]
复制
示例3
输入:
[0,1,2,1,2],3
复制返回值:
[0,1,1]
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param input int整型一维数组
* @param inputLen int input数组长度
* @param k int整型
* @return int整型一维数组
* @return int* returnSize 返回数组行数
*/
void quick_sort(int* input, int left,int right)
{
int i = left, j = right;
int tmp;
tmp = input[i];
if(i < j) {
while(i < j){
while(i < j && input[j] > tmp) {
j--;
}
if(i < j){
input[i] = input[j];
i++;
}
while(i < j && input[i] < tmp) {
i++;
}
if(i < j) {
input[j] = input[i];
j--;
}
}
input[i] = tmp;
quick_sort(input,left,i-1);
quick_sort(input,i+1,right);
}
}
int* GetLeastNumbers_Solution(int* input, int inputLen, int k, int* returnSize ) {
// write code here
int i = 0;
quick_sort(input, 0, inputLen-1);
// for(i = 0 ;i < k; i++){
// printf("%d\n",input[i]);
// returnSize[i] = input[i];
// }
*returnSize = k;
return input;
}