练习1：行动（Action）操作算子方法

任务1: reduce

// 1. 数组
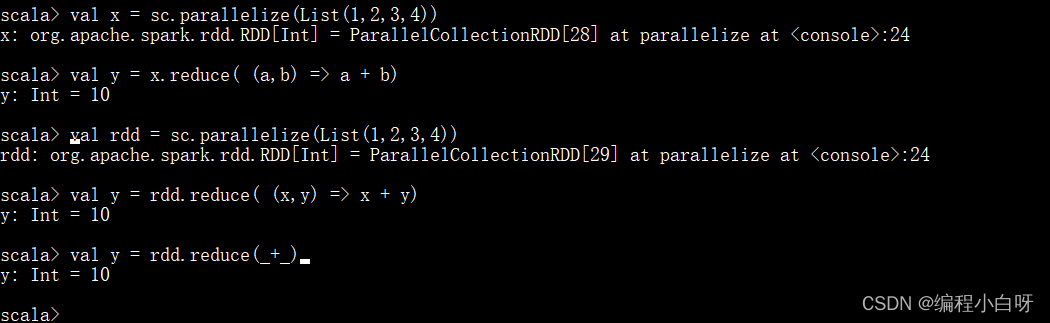
val x = sc.parallelize(List(1,2,3,4))
val y = x.reduce( (a,b) => a + b)
// 2. 列表
val rdd = sc.parallelize(List(1,2,3,4))
// 求和,将各个数累加,依次合并  下面两种方式相同
val y = rdd.reduce( (x,y) => x + y)
val y = rdd.reduce(_+_)

任务2: saveAsTextFile

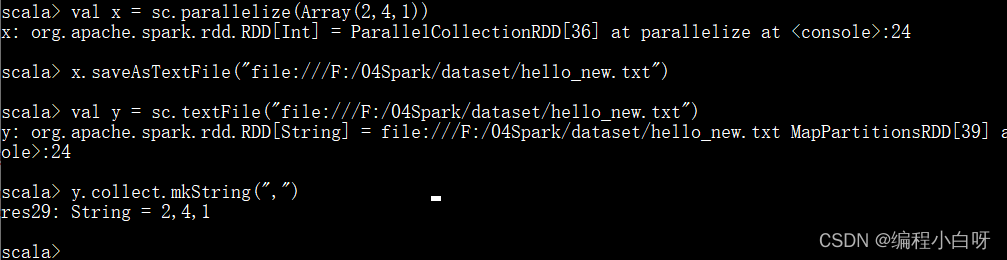
val x = sc.parallelize(Array(2,4,1))
x.saveAsTextFile("file:///F:/04Spark/dataset/hello_new.txt")
// 再将文件中内容读出来
val y = sc.textFile("file:///F:/04Spark/dataset/hello_new.txt")
y.collect.mkString(",")

练习2：RDD的分区操作、分区个数查看

任务1: textFile、parallelize

2.1 textFile

• 对于textFile而言，如果没有在方法中指定分区数，则sc.defaultMinPartitions默认为min(defaultParallelism,2)，其中，defaultParallelism对应的就是spark.default.parallelism，如果是从HDFS中读取文件，则分区数为文件分片数(比如，128MB/片)
• rdd的分区数 = max（本地file的分片数， sc.defaultMinPartitions）

// 1. 查看默认分区 （为4）
sc.defaultParallelism
// 2. 查看默认最小分区 （为2）
sc.defaultMinPartitions
//3.  将rdd存为文件
val rdd1 = sc.parallelize(Array(2,4))
rdd1.saveAsTextFile("file:///F:/04Spark/dataset/hello_new2.txt")
// 4. 读取
val rdd2 = sc.textFile("file:///F:/04Spark/dataset/hello_new2.txt")
// 5.查看分区的数量 （为4）
rdd2.partitions.size

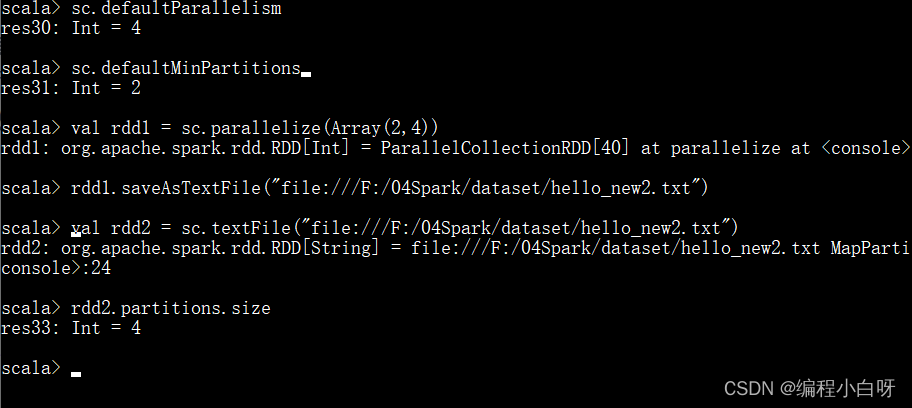
• 由于rdd的分区数 = max（本地file的分片数， sc.defaultMinPartitions），rdd的分区数为4，sc.defaultMinPartitions为2，所以本地file的分片数为4，检查发现确实分为4个part。

2.2 parallelize

• 这种方式下，如果在parallelize操作时没有指定分区数，则rdd的分区数 = sc.defaultParallelism

// 1. 没有设置分区数量
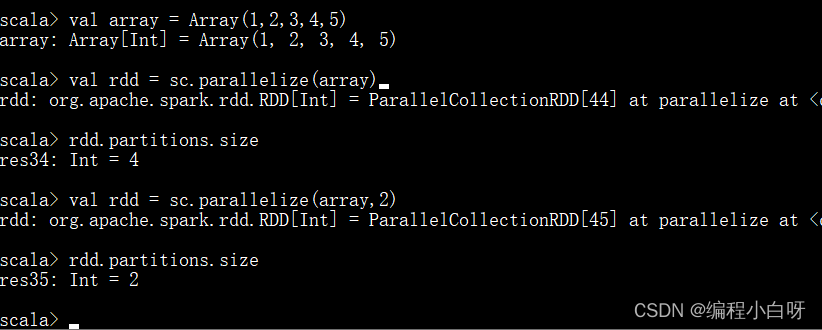
val array = Array(1,2,3,4,5)
val rdd = sc.parallelize(array) #没有设置分区数量
// 分区数量为默认分区数量（4）
rdd.partitions.size
// 2. 设置分区数量
val rdd = sc.parallelize(array,2) // 分区数量为2
// 结果分区数量变为2
rdd.partitions.size

任务2: repartition

• coalesce方法默认是不触发shuffle的，而repartition方法一定会触发shuffle，他们都可以重新进行分区
• repartition方法不会改变原来rdd分区数量，而是使返回新的rdd分区数量改变

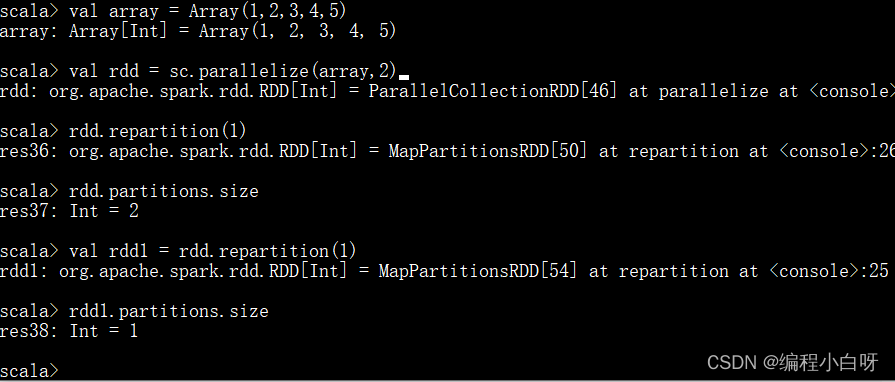
val array = Array(1,2,3,4,5)
val rdd = sc.parallelize(array,2) // 此时rdd分区数量为2
// repartition不会改变原来rdd，它会返回一个新的rdd
rdd.repartition(1)  // 此时rdd分区数量仍为2
rdd.partitions.size
// 返回一个新的rdd，新的rdd分区数量为1
val rdd1 = rdd.repartition(1) // 此时新的rdd1分区数量为1，rdd分区数量为2
rdd1.partitions.size

补充

1. countByKey()

• action算子；根据key的次数来做统计

val x = sc.parallelize(Array(('J',"James"),('F',"Fred"),('A',"Anna"),('J',"John")))
val y = x.countByKey()
println(y) 

2. foreachPartition

foreachPartition方法是迭代器被传入了我们的方法(每个分区执行一次函数，我们获取迭代器后需要自行进行迭代处理)

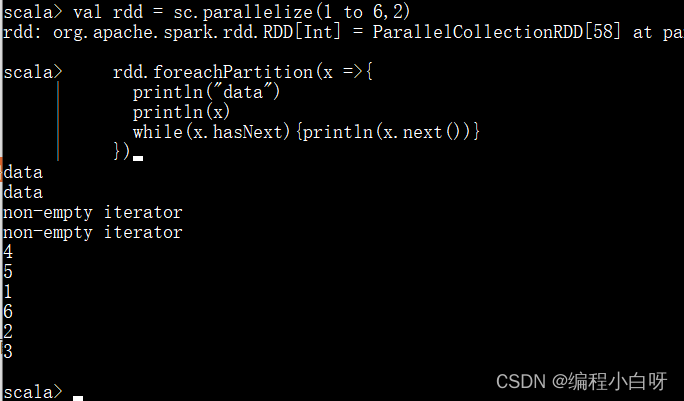
//   1. 分区 2个分区
    val rdd = sc.parallelize(1 to 6,2)
    rdd.foreachPartition(x =>{
      println("data")
      println(x)
      while(x.hasNext){println(x.next())}
    })

3. aggregate 方法

3.1 方法说明

首先对每个分区内的数据基于初始值进行一个首次聚合，然后将每个分区聚合的结果，通过使用给定的聚合函数，再次基于初始值进行分区之间的聚合，并且最终返回结果。该算子为action算子。

3.2 操作步骤

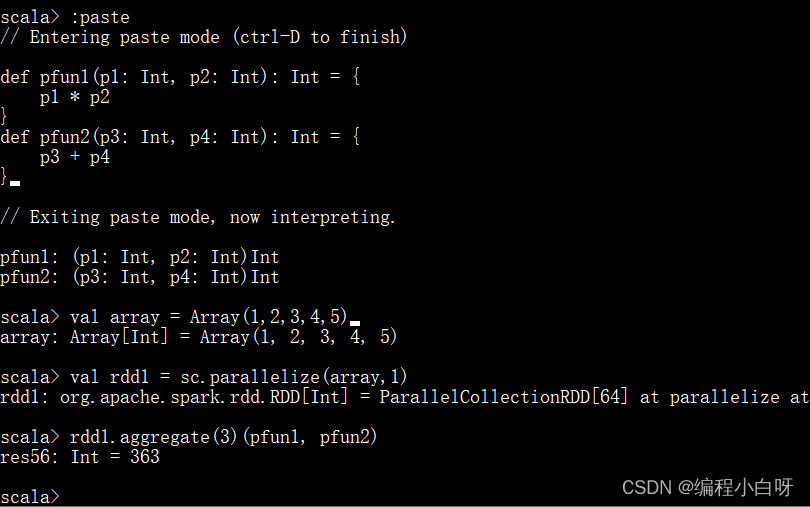
• 定义两个要给 aggregate 当作输入参数的函数,给初值3

// 乘积
def pfun1(p1: Int, p2: Int): Int = {
    p1 * p2
}
// 和
def pfun2(p3: Int, p4: Int): Int = {
    p3 + p4
}
// 
val array = Array(1,2,3,4,5)
// 指明分区数量为1，否则默认分区数量为4
 val rdd1 = sc.parallelize(array,1)
// 给定初值3，先进行相乘，再将结果进行相加
rdd1.aggregate(3)(pfun1, pfun2)

3.2 分析

• 首先用初值 3 作为 pfun1 的参数 p1 ，用 RDD 中的第 1 个值，即 1 作为 pfun1 的参数 p2 。由此我们可以得到第一个计算值为 3 * 1 = 3 。接着这个结果 3 被当成 p1 参数传入，RDD 中的第 2 个值即 2 被当成 p2 传入，由此得到第二个计算结果为 3 * 2 = 6 。以此类推，整个 pfun1 函数执行完成以后3 * 1 * 2 * 3 * 4 * 5 = 360

• 在 aggregate 方法的第 1 个参数函数 pfun1 执行完毕以后，我们得到了结果值 360 。于是，这个时候就要开始执行第 2 个参数函数 pfun2 了。

• pfun2 的执行过程与 pfun1 是差不多的，同样会将 zeroValue 作为第一次运算的参数传入，在这里即是将 zeroValue 即 3 当成 p3 参数传入，然后是将 pfun1 的结果 360 当成 p4 参数传入，由此得到计算结果为 363 。因为 pfun1 仅有一个结果值，所以整个 aggregate 过程就计算完毕了，最终的结果值就是 363 。
  注意分区数量的不同导致最后运算的结果也会不同。

3.3 多个分片RDD

val array = Array(1,2,3,4,5,6,7,8,9,10)
val rdd2 = sc.parallelize(array,3)
rdd2.getNumPartitions

rdd2.aggregate(2)(pfun1, pfun2)

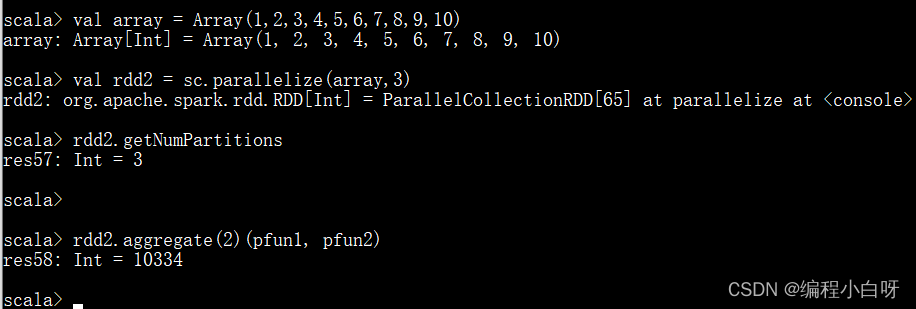
• 分析：
  2 * 1 * 2 * 3 = 12
  2 * 4 * 5 * 6 = 240
  2 * 7 * 8 * 9 * 10 = 10080
  2 + 12 + 240 + 10080 = 10334

参考链接

1. aggregate参考
2. 默认分区数参考