论文地址：Delving into Localization Errors for Monocular 3D Object Detection
Github地址：Delving into Localization Errors for Monocular 3D Object Detection

1. 解决了什么问题？

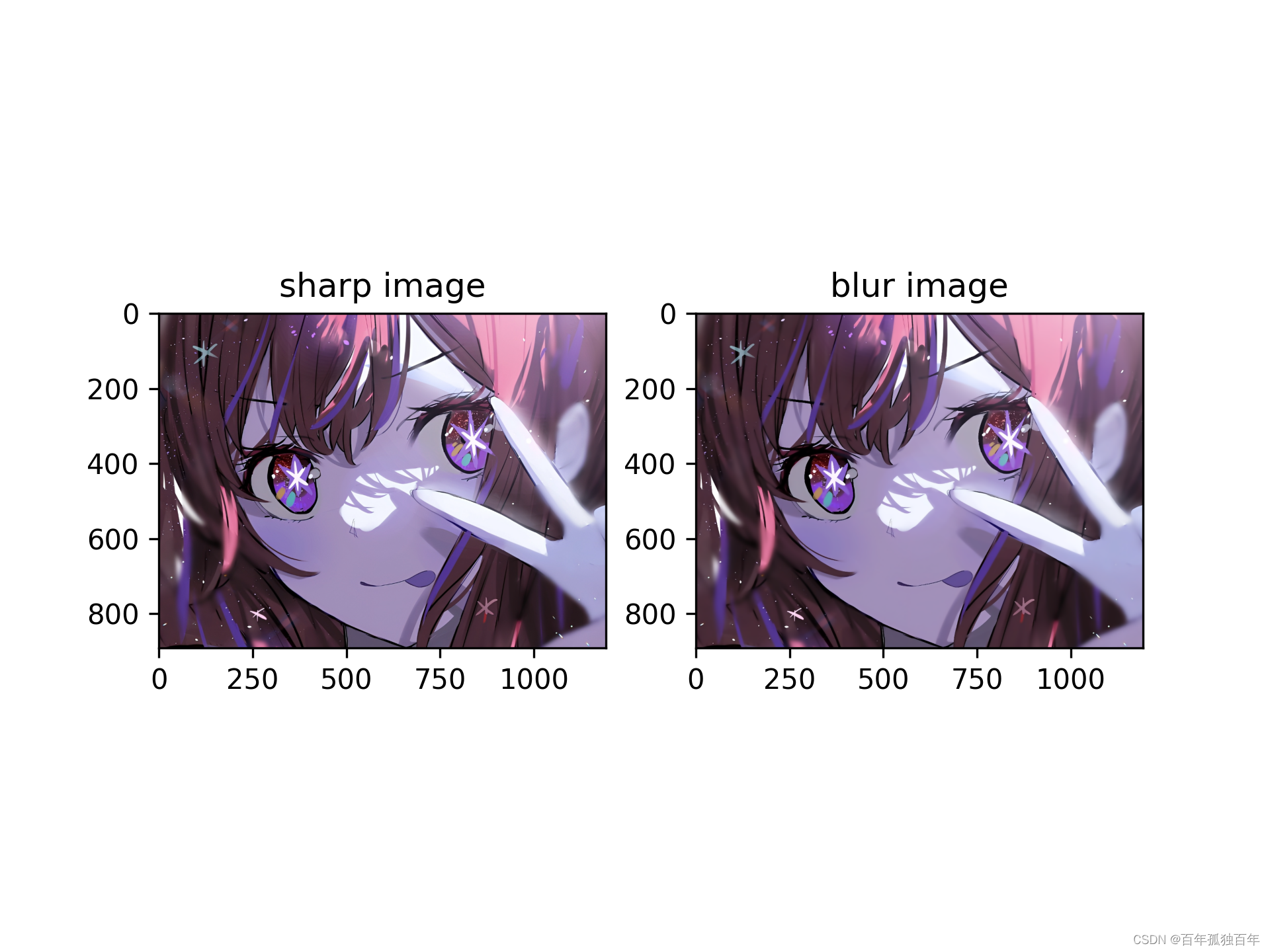
从单目图像准确地估计 3D 框是自动驾驶领域的重要功能，但很具有挑战性。本文以 CenterNet 为基线模型，逐个地将预测项替换为 ground-truths。为了更好地分析误差的规律，作者以深度范围的方式做评测，在下图展示了各实验的结果。下图是在 KITTI 验证集上做的评测，用 Car 类别的${\text{AP}}_{40}$作为指标，采样区间是$10m$。比如，横轴上的$20$表示样本的整体表现在$15m$到$25m$区间。作者有三点发现：

• 使用 ground-truth location 时，表现的提升最明显，甚至接近 LiDAR 方法的表现，这说明定位误差是制约 3D 检测的关键因素。此外，除了深度估计，检测到 3D 目标的投影中心点对于恢复目标的 3D 位置也很重要。CenterNet 将 2D 框中心点当作 3D 框在图像平面的投影中心，然后用预测的深度和相机参数反投回到 3D 空间。但是，2D 框中心和 3D 框的中心并不一样，于是，作者探讨了 2D 框中心和 3D 目标投影中心不对齐的问题，认为应该在单目 3D 检测器中保留 2D 检测分支，用 3D 投影中心替换 2D 框的中心能提升定位的准确率。2D 检测作为辅助任务，有助于特征学习。
• 随着目标的距离增大，检测准确率会显著降低。超过一定的距离后，所有的模型都无法准确预测目标。作者发现，现有的方法都受到定位误差影响，无法准确地检出远距离物体。因此，作者认为可以从训练集中去除这些目标。“坏”样本和“容易检测”的样本之间有明显的域差异，强迫网络学习这些样本会降低其表征能力，不利于网络的整体表现。于是作者将远距离样本从训练集中剔除，并降低这些样本的损失权重。
• 除了定位误差，尺寸估计也束缚了单目 3D 检测的表现（即便用了 ground-truth location，仍有$27.4\%$的提升空间）。现有的方法单独优化 3D 框的每个部分，但没有在一个最终的度量（即 3D IoU）里考虑每个损失项，这种优化并不是最优的。于是作者提出了 IoU 朝向损失来做尺寸预测。该损失根据样本的每一个面对 3D IoU 的贡献，动态地调节它的损失权重。

2. 提出了什么方法？

本文通过大量的消融实验，对每个子任务做定量分析，发现定位误差是制约单目 3D 检测重要的因素。作者也研究了造成定位误差的底层原因，分析它们带来的问题，从而提出了三个策略。

• 2D 框中心点和 3D 目标的投影中心点之间存在不对齐的问题，这会造成定位准确率偏低。
• 用现有的方法要想定位远距离物体，几乎是不可能的，远距离目标会误导网络的学习。作者认为应将这些样本从训练数据集中去除，从而提升检测器的整体表现。
• 针对目标的尺寸估计任务，作者提出了 3D IoU 朝向损失，它不会受到“定位误差”影响。

2.1 问题定义

给定一张 RGB 图像及相机参数，我们要对 3D 空间中感兴趣的目标做分类和定位。每个目标都有它的类别、2D 框${\mathbf{B}}_{2D}$、3D 框${\mathbf{B}}_{3D}$。${\mathbf{B}}_{2D}$用中心点${\mathbf{c}}^{\mathbf{i}}=[x^{\prime },y^{\prime }{]}_{2D}$和图像平面的尺寸$[h^{\prime },w^{\prime }{]}_{2D}$表示，而${\mathbf{B}}_{3D}$用它在 3D 世界空间的中心$[x,y,z{]}_{3D}$、尺寸$[h,w,l{]}_{2D}$和朝向角$\gamma$表示。

2.2 基线模型

架构

作者基于单阶段 anchor-free 的 CenterNet 构建基线模型。主干网络为 DLA-34，它平衡了速度和精度。然后是七个轻量级的 heads（由一个$3\times 3$卷积层和$1\times 1$卷积层实现），分别用于 2D 检测和 3D 检测。

2D 检测

模型输出热力图，表示分类得分和目标大概的中心位置$\mathbf{c}=(u,v)$。$\mathbf{c}$用 ground-truth 2D 框的中心点的坐标监督。另一个分支则预测$\mathbf{c}$和实际中心位置的偏移量${\mathbf{o}}^{\mathbf{i}}=(\Delta u^i,\Delta v^i)$，然后得到最终的 2D 框中心坐标${\mathbf{c}}^{\mathbf{i}}=\mathbf{c}+{\mathbf{o}}^{\mathbf{i}}$。最后，还有一个分支预测 2D 框的尺寸$[w^{\prime },h^{\prime }{]}_{2D}$。

3D 检测

一个分支预测$\mathbf{c}$和 3D 框中心投影${\mathbf{c}}^{\mathbf{w}}$(${\mathbf{c}}^{\mathbf{w}}=[x^w,y^w{]}^T=\mathbf{c}+{\mathbf{o}}^{\mathbf{w}}$) 之间的偏移量${\mathbf{o}}^{\mathbf{w}}=(\Delta u^w,\Delta v^w)$。通过相机参数$\mathbf{K}\in {\mathbb{R}}^{3\times 3}$，我们可以恢复 3D 世界中目标的中心位置：
$${\left[\begin{array}{c}x\\ y\\ z\end{array}\right]}_{3D}={\mathbf{K}}^{-1}\left[\begin{array}{c}{\mathbf{c}}^{\mathbf{w}}\cdot z\\ z\end{array}\right]={\mathbf{K}}^{-1}{\left[\begin{array}{c}{x}^w\cdot z\\ y^w\cdot z\\ z\end{array}\right]}_{2D}$$
$z$是深度分支预测的值。其余两个分支分别预测 3D 尺寸$[h,w,l{]}_{3D}$和朝向角$\gamma$。
损失
总共有七项损失，一个用于正负样本分类，两个（中心位置和尺寸）用于 2D 检测，四个（中心位置、深度、尺寸、朝向角）用于 3D 检测。

• 分类任务使用了 Focal Loss。
• 对于 2D 检测的中心位置和尺寸回归，使用了 L1 损失。
• 对于 3D 检测，
  • 用不确定性建模深度估计，
  • 3D 中心坐标优化采用了 L1 损失，
  • 朝向角估计使用了 multi-bin loss（考虑了$12$个不重叠的 bins），
  • 尺寸估计使用了 L1 损失，以及本文提出的 IoU 损失。
    所有损失项权重都是$1$。

2.3 误差分析

作者探究了制约单目 3D 检测表现的因素。作者在 KITTI 验证集上进行误差分析，将每一项预测结果替换为 ground-truths，然后评测其表现。如上表所示，如果将预测的 3D 中心${\mathbf{c}}^{\mathbf{w}}$替换为 ground-truths，准确率从$11.12\%$提升到了$18.97\%$。此外，ground-truth 深度值可以将准确率提升至$38.01\%$。如果深度和 3D 中心投影都考虑了，再将预测 3D 坐标$[x,y,z{]}_{3D}$替换为 ground-truths 能带来最显著的提升。所以作者认为，单目 3D 检测效果差，主要是定位误差造成的。根据上式，深度估计和中心位置一起决定了 3D 空间内目标的位置。在单目图像中做深度估计是不适当的，优化中心点的检测效果是更加合理的努力方向。

上表展示了图像平面（以像素为单位）上中心点偏移造成的定位误差（以米为单位）。KITTI 数据集中，cars 的平均尺寸$[h,w,l{]}_{3D}$为$[1.53m,1.63m,3.53m]$。假设其它的度量都是对的，用长度$l$来对齐定位误差，IoU 计算过程为：
$IoU=\frac{3.53-{\Delta }_{loc}}{3.53+{\Delta }_{loc}}$
其中${\Delta }_{loc}$表示定位误差。IoU 阈值设定为$0.7$，因此理论可接受的最大误差是$0.62m$。但是，图像上$4\sim 8$个像素（$4\times$下采样的特征图上$1\sim 2$像素）的误差都会造成相距$60m$的物体无法被准确检测到。再加上其它任务的误差（比如下图的深度估计误差），要想在单目图像上准确地检测远距离 3D 物体几乎就是不可能的，除非深度信息是非常准确的。下图的上半部分是 2D 框中心和 3D 投影到图像平面的中心不对齐的现象（以像素为单位，来源于 KITTI trainval 集）；下半部分是深度误差（以米为单位，用 KITTI 训练集训练，在验证集测试）。

2.4 Revisiting Center Detection

Our design for center detection

为了预测目标大概的中心位置$\mathbf{c}$，本文提出的方法很简单。

• 将投影 3D 中心点${\mathbf{c}}^{\mathbf{w}}$作为预测中心位置$\mathbf{c}$分支的 ground-truths，
• 迫使模型同时去学习 2D 检测的特征。
  这些设计来自于下面的分析：
• 分析1：如下图所示（红色为 3D 投影中心，蓝色为 2D 框中心），在 2D 框中心${\mathbf{c}}^{\mathbf{i}}$和 3D 框中心投影${\mathbf{c}}^{\mathbf{w}}$之间存在不对齐的现象。3D 投影中心点${\mathbf{c}}^{\mathbf{w}}$是恢复 3D 目标中心$[x,y,z{]}_{3D}$的关键。那么问题就是$\mathbf{c}$的监督信号应该是什么。一些论文将 2D 框中心${\mathbf{c}}^{\mathbf{i}}$作为标签使用，但${\mathbf{c}}^{\mathbf{i}}$和 3D 目标中心的关联并不紧密，使得中心点预测并不清楚目标的 3D 几何信息。因此，作者将 3D 投影中心${\mathbf{c}}^{\mathbf{w}}$作为训练$\mathbf{c}$的 ground-truths。
• 分析2：SMOKE 算法也将 3D 投影中心${\mathbf{c}}^{\mathbf{w}}$作为中心点$\mathbf{c}$的 ground-truth 标签。但是它抛弃了 2D 检测分支，而本文选择保留该分支。在本方法中，用 3D 投影中心${\mathbf{c}}^{\mathbf{w}}$监督$\mathbf{c}$，也负责监督预测 2D 框的中心${\mathbf{c}}^{\mathbf{i}}$。此外，2D 检测分支会预测一个真实 2D 中心和预测中心$\mathbf{c}$之间的偏移量${\mathbf{o}}^{\mathbf{i}}={\mathbf{c}}^{\mathbf{i}}-\mathbf{c}$。这样，模型就知道了目标的几何信息。然后，还有一个分支预测 2D 框的大小，共享特征就能学到一些有利于深度估计的信息。这样，保留了 2D 检测有助于 3D 特征学习。
  

2.5 训练样本

本文认为去掉那些极端困难的样本对于单目 3D 检测网络的整体表现是有益的。物体的距离和检测难易程度之间是强关联的。于是，作者设计了两种机制，计算样本$i$的训练权重$w_i$：

• 硬编码，该机制舍弃那些超出一定距离的样本：
  $w_i=\{\begin{array}{rlr}1,& \text{if}& d_i\le s\\ 0,& \text{if}& d_i>s\end{array}$
  $d_i$表示样本$i$的深度，$s$是深度阈值，在实验中设为$60m$。凡是距离超出$s$的样本不参与训练。
• 软编码，用近似于 sigmoid 的函数计算，
  $w_i=\frac{1}{1+e^{(d_i-c)/T}}$
  $c$和$T$是超参数，调节对称中心和弯曲度。当$c=s,T\to 0$时，等价于硬编码。当$T\to \infty$，所有的样本的权重一样。默认$c=60,T=1$。
  这两个机制效果差不多。

2.6 IoU Oriented Optimization

在单目 3D 检测中，判断物体的 3D 中心是很难的，定位误差经常能达到几米远。直接用 IoU 损失，会使定位相关的任务（如深度估计）比其它任务（如 3D 尺寸预测）更加重要。然而单目图像做深度估计是不适合的，该矛盾会造成训练的效果比较差。另一方案是将每个损失解耦开来，再独立地优化，但它忽视了损失项彼此之间的联系。于是，作者针对 3D 尺寸预测提出了 IoU oriented 优化方法。假设所有的预测项（除了 3D 尺寸$\mathbf{s}=[h,w,l{]}_{3D}$）都是对的，我们可得到：
$\frac{\partial IoU}{\partial h}:\frac{\partial IoU}{\partial w}:\frac{\partial IoU}{\partial l}\approx \frac{1}{h}:\frac{1}{w}:\frac{1}{l}$
该等式证明可见于2.9。因此，我们可以根据 IoU 的偏导数来调节每一项的权重，3D 尺寸估计的损失函数可变形为：
${\mathcal{L}}_{size}={\Vert \frac{(\mathbf{s}-{\mathbf{s}}^{\ast })}{\mathbf{s}}\Vert }_1$
${\Vert \cdot \Vert }_1$表示 L1 范数。注意，与标准的 3D 尺寸损失函数${{\mathcal{L}}^{\prime }}_{size}=\Vert \mathbf{s}-{\mathbf{s}}^{\ast }\Vert$，该新损失的数量级没有改变。重新计算一次${{\mathcal{L}}^{\prime }}_{size}$，计算补偿权重$w_s=|{{\mathcal{L}}^{\prime }}_{size}/{\mathcal{L}}_{size}|$，最终损失函数$w_s\cdot {\mathcal{L}}_{size}$的均值等于${{\mathcal{L}}^{\prime }}_{size}$。因此，本文提出的损失可以看作为标准 L1 损失的重新排布。

2.7 实现

训练

在两张 GTX 1080Ti 显卡训练，batch size 为$16$，训练了$140$个 epochs。使用 Adam 优化器，初始学习率为$1.25e^{-3}$，在第$90$和$120$个 epoch 时乘以$0.1$衰减。Weight decay 为$1e^{-5}$，在前$5$个 epochs 使用 warmup 策略。为避免过拟合，使用了随机裁剪和缩放（只针对 2D 检测）和随机水平翻转。整个训练花费了$9$个小时。

推理

从两个解码器得到预测结果。使用$3\times 3$最大池化对中心点检测结果做 NMS。然后，恢复出 2D/3D 框，中心点的得分作为预测结果的得分。丢弃那些置信度$<0.2$的预测结果。

2.8 Uncertainty Modeling

对深度估计使用异方差偶然不确定性建模。同时预测深度$\mathbf{d}$和标准差$\sigma$：
$[\mathbf{d},\sigma ]=f^{\mathbf{w}}(\mathbf{x})$
$\mathbf{x}$是输入数据，$f$是卷积网络，参数为$\mathbf{w}$。然后，使用 Laplace 似然来建模不确定性，深度估计的损失写作：
$\mathcal{L}=\frac{\sqrt{2}}{\sigma }{\Vert \mathbf{d}-{\mathbf{d}}^{\ast }\Vert }_1+\log \sigma$
${\Vert \cdot \Vert }_1$表示 L1 范数，${\mathbf{d}}^{\ast }$是 ground-truth 深度值。类似地，高斯似然建模的损失写作：
$\mathcal{L}=\frac{1}{2{\sigma }^2}{\Vert \mathbf{d}-{\mathbf{d}}^{\ast }\Vert }_2+\frac{1}{2}\log {\sigma }^2$
${\Vert \cdot \Vert }_2$表示 L2 范数。
从下表可以看到，不确定性建模可以提升深度图的准确率，从而提升整体表现。此外，基于 Laplace 分布建模的不确定性要比高斯分布更适合深度预测任务。

2.9 IoU Oriented Loss

Proposition

假设所有的预测项都是完全正确的（除了 3D 尺寸$(h,w,l)$），3D IoU 每一项的贡献率$\frac{\partial IoU}{\partial h}:\frac{\partial IoU}{\partial w}:\frac{\partial IoU}{\partial l}\approx \frac{1}{h}:\frac{1}{w}:\frac{1}{l}$。
证明
给定上述条件，3D IoU 可以写作：
I o U = Π i ∈ { h , w , l } min ⁡ ( i , i ∗ ) h × w × l + h ∗ × w ∗ × l ∗ − Π i ∈ { h , w , l } min ⁡ ( i , i ∗ ) IoU=\frac{\Pi_{i\in\left\{h,w,l\right\}}\min(i,i^\ast)}{h\times w\times l+h^\ast\times w^\ast\times l^\ast - \Pi_{i\in\left\{h,w,l\right\}}\min(i,i^\ast)} IoU=h×w×l+h∗×w∗×l∗−Πi∈{h,w,l}​min(i,i∗)Πi∈{h,w,l}​min(i,i∗)​
这里$(h^{\ast },w^{\ast },l^{\ast })$表示预测的 3D 尺寸$(h,w,l)$对应的 ground-truths。对于 3D 尺寸的预测值和 ground-truth 值之间的不同关系，可以分为下述情形：

• 如果$h\le h^{\ast },w\le w^{\ast },l\le l^{\ast }$，上式可简化为：$IoU=\frac{h\times w\times l}{h^{\ast }\times w^{\ast }\times l^{\ast }}$，计算 3D IoU 关于高度$h$的偏导$\frac{\partial IoU}{\partial h}=\frac{w\times l}{h^{\ast }\times w^{\ast }\times l^{\ast }}$，$\frac{\partial IoU}{\partial w},\frac{\partial IoU}{\partial l}$情况类似。然后，将它们的偏导数结合起来，每个的贡献率就是$\frac{\partial IoU}{\partial h}:\frac{\partial IoU}{\partial w}:\frac{\partial IoU}{\partial l}=\frac{1}{h}:\frac{1}{w}:\frac{1}{l}$。
• 如果$h>h^{\ast },w>w^{\ast },l>l^{\ast }$，可以推导出相同的结论。
• 如果$h>h^{\ast },w\le w^{\ast },l\le l^{\ast }$，3D IoU 表示为$IoU=\frac{h^{\ast }\times w\times l}{h\times w\times l+h^{\ast }\times w^{\ast }\times l^{\ast }-h^{\ast }\times w\times l}$，计算 3D IoU 关于$h,w,l$的偏导数，可以得到每个的贡献率为$\frac{\partial IoU}{\partial h}:\frac{\partial IoU}{\partial w}:\frac{\partial IoU}{\partial l}=\frac{w\times l}{h^{\ast }\times w^{\ast }\times l^{\ast }}:\frac{1}{w}:\frac{1}{l}$。
• 如果$h>h^{\ast },w>w^{\ast },l\le l^{\ast }$，可以得到 $IoU=\frac{h^{\ast }\times w^{\ast }\times l}{h\times w\times l+h^{\ast }\times w^{\ast }\times l^{\ast }-h^{\ast }\times w^{\ast }\times l}$，3D IoU 关于每一项的贡献率为$\frac{\partial IoU}{\partial h}:\frac{\partial IoU}{\partial w}:\frac{\partial IoU}{\partial l}=\frac{1}{h}:\frac{1}{w}:\frac{h^{\ast }\times w^{\ast }\times l^{\ast }}{h\times w\times l\times l}$。
  其它情形与上述第3和第4个类似。当$h\approx h^{\ast },w\approx w^{\ast },l\approx l^{\ast }$，可以得到$\frac{\partial IoU}{\partial h}:\frac{\partial IoU}{\partial w}:\frac{\partial IoU}{\partial l}\approx \frac{1}{h}:\frac{1}{w}:\frac{1}{l}$。