文章目录

part1. Data path设计
- 1.1 logic unit
- 1.2 shifter
- 1.3 adder
- 1.4 comparator
- 1.5 multiplier
- 1.6 divider
- 1.7 register file
part2. Control unit设计
part3. CPU SoC上的其它部件 (TODO：理解总结)
- 3.1 总线
- - AMBA（parallel）
- 3.2 Memory
- - memory 的分级结构

PPT: 7,8,9,10,11,12

part1. Data path设计

data path的功能是用于执行指令处理数据，虽然说在处理器核的结构示意图中画出了data memory和instruction memory，但是这个memory实际上并不属于处理器本身而是像io等设备一样属于SoC。因此在处理器中只需要处理如何从memory中存取数据的问题了，并不需要过多考虑memory实际的设计。

1.1 logic unit

这个部件，用于在ALU中进行逻辑运算。显然根据其功能我们可以做出下面的原型：

fig1. logic unit prototype

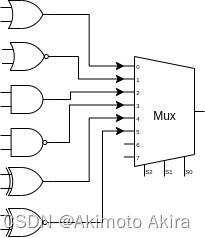
然而这个结构不能满意，主要是因为右边这个巨大的mux。其简化的真值表可以表示如下：

s0	s1	s2	s3	function
0	0	0	1	AND
1	1	1	0	NAND
0	1	1	1	OR
1	0	0	0	NOR
0	1	1	0	XOR
1	0	0	1	XNOR

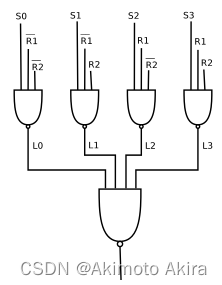
化简之后可得 $logic\_out=\overline{s0 \cdot \bar{R1} \cdot \bar{R2}} + \overline{s1 \cdot \bar{R1} \cdot R2} + \overline{s2 \cdot R1 \cdot \bar{R2 } }+ \overline{s3 \cdot R1 \cdot R2}$ 。其中R1，R2为logic unit的输入。也可以化为用NAND逻辑表示的逻辑电路。

fig2. UltraSpark T2 logic unit

1.2 shifter

固定带宽的移位寄存器如图fig3所示。这种移位寄存器需要时钟信号的驱动，每一个时钟周期后都会将数据移位一次。这个实际的用途还是用于存储数据而不是作移位计算
，因此并不是我们希望的shifter。

fig3. shift register

在ALU中由于需要在一个周期内将移位工作完成。在这个结构中，因为只有组合逻辑，因此理想状态下是当有输入时就有对应的输出。其功能描述对应的vhdl如下所示：

library ieee;
use ieee.std_logic_1164.all;

entity shifter is 
	port (
		data_in: in std_logic_vector(31 downto 0);
		shiift_select: in std_logic_vector(3 downto 1);
		data_out: out std_logic_vector(31 downto 0);
	);
end entrity;
architecture rtl of shifter is
	begin
	case shift_select is --通过选择引脚的配置决定移位多少位
		when "100" =>
			data_out(31)<='0' --或者这里data_out(31)<=data_in(0)实现循环移位
			gen_shift_1b: for i in 0 to 30 generate
				data_out(i)<=data_in(i+1); --实现data_in的右移1位
		when "010" =>
			...
		when "001" =>
			...
	end case;
end rtl;

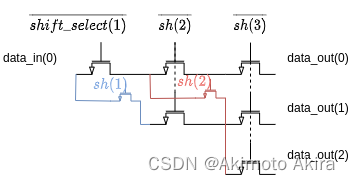
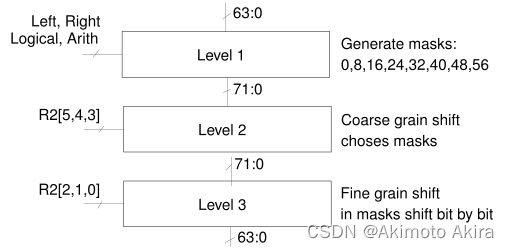
一个简化的结构示意图fig4所示，图中表示的是在不同的shift_select配置下data_in(1)信号的流向，也是实际上ASIC综合之后的transistor level description。

fig4. shift register transistor level description 在UltraSpark T2中的shifter的设计如图fig5所示，其中包括3个stage，其中第一个stage处理左右移位逻辑移位和算术移位的配置问题并生成跨度为0,8,16,...,56的跨度较大的模板结果，第二个stage则是对模板结果进行选择并生成0,1,2,3,...,8位的移位结果，最后在第三个stage中对移位结果进行选择从而生成最后结果。就功能本身分析这个shifter实现了sll,sllx,srl,sra,srlx,srax指令功能。需要注意的是逻辑移位和算术移位的区别在于对有符号数的处理，逻辑移位在右移的时候左边的符号位不需要扩展直接填0，而算术移位填上的是符号位上一样的数。

fig5. UltraSpark T2 shifter

1.3 adder

ripple carry adder是最基本最原始的加法器其原理是基于全加器如下所示：
$S_{i}=A_{i} \oplus B_{i} \oplus C_{i} (C_{i}是外部输入的进位) \\ C_{i+1}=A_i \cdot B_i + A_i \cdot C_i + B_i \cdot C_i$
其结构如图fig6所示，由图可知每次在计算的时候高位的结果总需要在低位的进位结果计算完之后才能计算出来，因此第一个改进则是将低位的结果和高位结果并行计算，对于高位的结果可以生成低位进位的两种不同情况，即进位为0和进位为1的结果，然后当低位进位结果计算完之后用mux选出正确的高位结果即可。

fig6. RCA（ripple carry adder）

fig7. CSA（carry select adder）

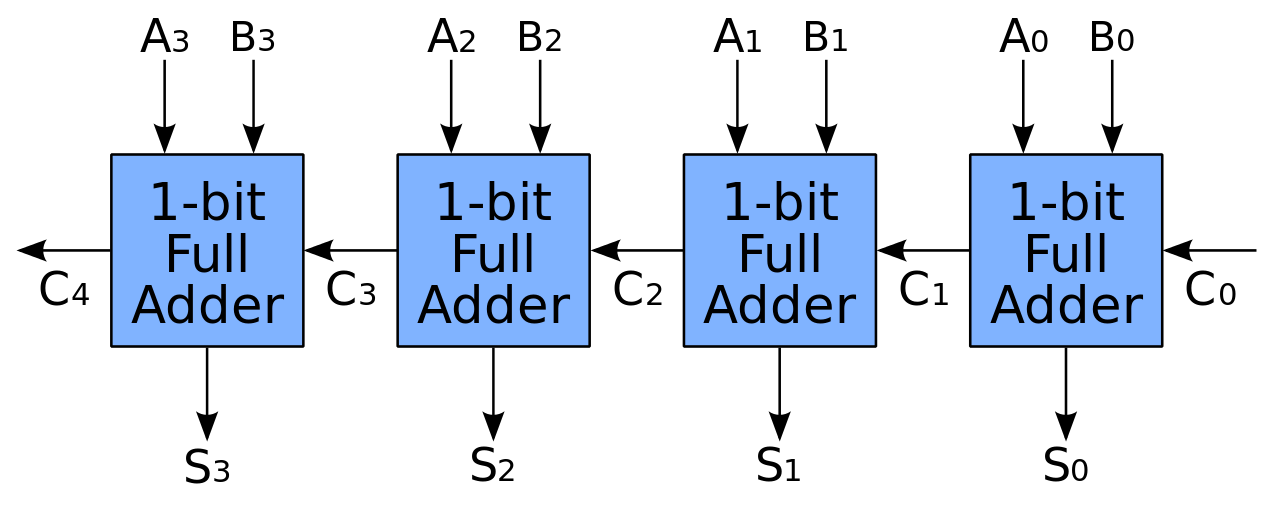
The idea behind the CLA(carry look ahead adder) is to compute several carries simultaneously and to avoid waiting until the correct carry propagates from the stage of the adder in which it has been generated.

在此有两个必须理解透彻的概念：propagate和generate（通过Carry skip adder的例子理解）

在carry skip adder中，为了避免进位延迟的问题，将n bit输入分为了k组进行上面提到的进位选择。第j+1组的进位输入由第j组决定是否延续j-1组以前的进位，如果p=1则表示carry是可以通过第j组传递到j+1组（即j-1的进位输出和j组的进位输出是一样的），如果p=0则表示不能传递过去，此时可以理解为第j组的RCA阻断了carry的传播或者说其carry_out和j-1组的carry_out是不一样的。
知道propagate的概念后，可以理解carry skip adder的主要思路是当第j组的进位是可以传递j-1组的进位时（p=1），j+1组的结果就不需要等待第j组的进位生成后再运行，而是直接使用j-1组的进位信号（即bypass第j组的进位）。

我们现在缩小我们的视野放在第j组RCA的一个位上，在第i+1位上的进位输入可以写成： $C_{i+1}=A_i \cdot B_i+ A_i \cdot C_i + B_i \cdot C_i=A_i \cdot B_i+C_i \cdot (A_i + B_i)$
其中：

$p_i=A_i + B_i$ ：当这个为1时表示i组的carry_in = carry_out
$g_i=A_i \cdot B_i$ ：当这个为1时表示carry_out由i组的RCA自己生成

那么也就是说，如果想要第j组的carry out=carry in那么我们需要其所有位上的p全都为1，此时第j+1个RCA就可以使用第j-1个RCA的进位了。carry skip adder结构示意图fig8所示

fig8. carry skip adder

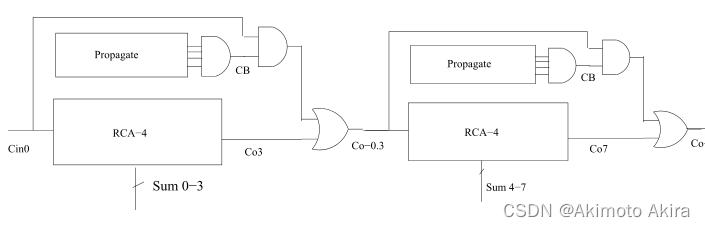
由上面加法器的逻辑运算式和propagate和generate的定义，可以将 $C_i$ 中的 $C_{i-1}$ 一直嵌套直到 $C_0$ ：
$C_i=g_i+p_i\cdot C_{i-1}=g_i+p_i\cdot (g_{i-1}+p_{i-1}\cdot C_{i-2})=...$
也就是说当 $C_0$ 已知时，只需要再知道输入是什么立即可以知道所有位上的进位取值，根据 $C_{i-1}$ 可以用下面公式计算出 $S_i$ 的值：
$S_i=A_i \oplus B_i \oplus C_{i-1}$
前面这个 $A_i \oplus B_i=p_i$ 成立是因为下面加法器的真值表，用xor定义propagate是更加严格的方式，因为在中间的第2，3，6，7行中才有 $C_i=C_o$ 。那么我们如果用 $\cdot b ; p=a \oplus b$ 定义这两个概念时就是说没有考虑a=0, b=0的情况，因为表中列出的两种情况下 $\oplus b=a + b$ ，因此这样的替代对是否跳过当前的RCA判断并没有影响，与此同时这个异或的结果还能直接用到结果运算中去，可以说是一石二鸟的做法：

fig9. 加法器真值表

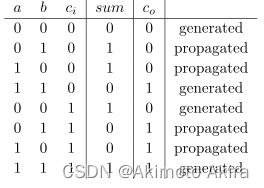
由此根据上面两个式子可以设计出由 $p_i$ 和 $g_i$ 计算的carry look ahead adder的原型如图fig10所示。显然这个方法下一旦输入的位宽稍大逻辑电路的复杂程度就会非常高，因此还需要进一步改进。

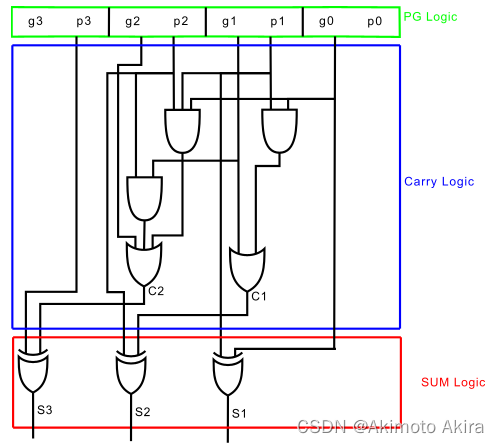
fig10. prototype of carry look ahead adder 除此之外还有另一种实现方法跟ripple carry adder一样的逻辑，一位一位用相同的结构连起来。如图fig11 所示，然而这样的好处就是逻辑门结构简单且规则，其复杂程度也不会随着输入带宽增加而增加。但是相比较上面的结构而言在g=0,p=1时还是需要高位等待低位的进位结果的。

fig11. different ripple look ahead adder implementation

此外在基于carry select adder的基础上我们可以使用PG block尽可能快地计算出每一个位加法操作的进位，carry network和adder network共同组成加法器电路即tree/prefix adder。对于上面的ripple carry look ahead adder我们可以将其换一种更清楚的表达方式如图fig12。

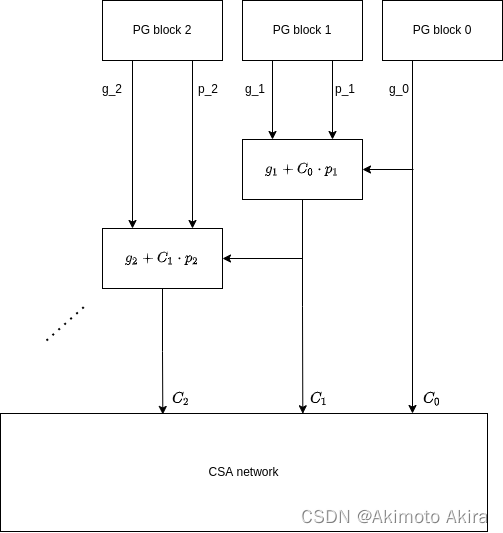
fig12. ripple carry look ahead adder implementation

在这里我们根据上面PG的形式，定义PG operator如下：
$G_{i:j} = {\color{blue}G_{i:k}}+{\color{blue}P_{i:k}} \cdot {\color{red}G_{k-1:j}} \\ P_{i:j} = {\color{blue}P_{i:k}} \cdot {\color{red}P_{k-1:j}}$
其中：

$G_{i:i}=g_i; P_{i:i}=p_i$
$g_0=c_{in}; p_0=0$
$\ge k>j$

由上面定义可知，实际上我们需要的 $C_i$ 就是上面对应的 $G_{i:0}$ 。然后根据上面定义的这个公式可以根据需求求出所需要的进位比如说需要 $C_6$ ，那么根据上面的式子我们可以得到，如果目前下面式子里的所有输入都已经算好了那么就可以直接连上如果没有的话就要再继续分解，一般来说 $PG_{x:x}$ 都是由最上层的输入计算得来的，因此我们需要关注的是 $G_{5:0}$ 是否存在，当 $G_{5:0}$ 没有计算出来时就需要对 $G_{5:0}$ 进行分解，一层一层往回推直到能用已知的输入表示为止：
$G_{6:0}=G_{6:6}+P_{6:6} \cdot G_{5:0}$

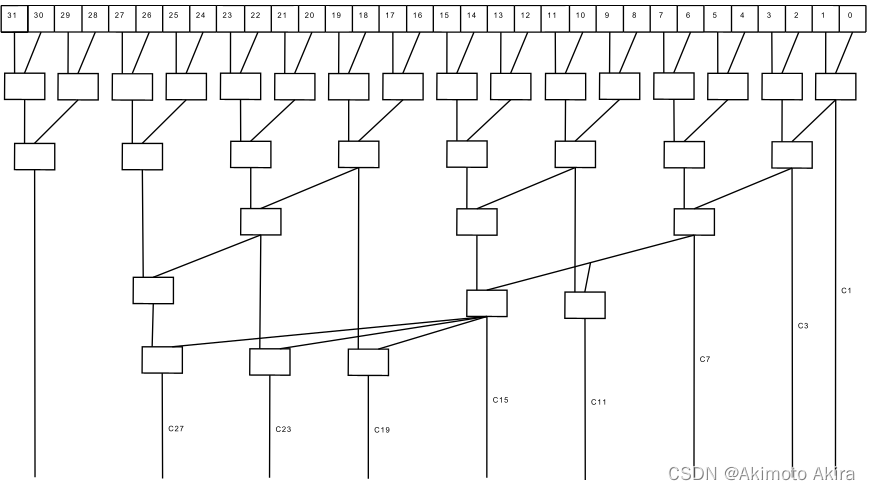
这个PG tree 可以由设计人员根据实际情况设计，不同的结构影响的是carry结果产生的时间，在Petium4中使用的tree结构如图fig13所示，类似的结构还有Kogge-Stone propagate network，Brent and Kung propagate network等。

fig13. Pentium 4 sparse tree propagate network

1.4 comparator

比较器主要的原理性的东西是数据之间的减法，然后对减法结果进行判断，因此需要依赖ALU进行操作。对此首先ALU必须要有减法操作，即 sub(operand_A, operand_B) = oprand_A + complement(operand_B)，然后需要检查cout的输出和ALU加法的输出。下面是比较器的检测逻辑：

条件	结果
z=1(ALU输出为0)	A=B
z=0	A!=B
c=1	A>=B
c=0	A<B
c=1, z=0	A>B
c=0, z=1	A<=B

其逻辑电路如图fig14所示：

fig14. comparator

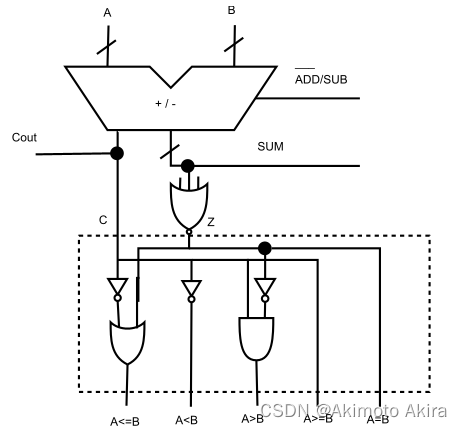
1.5 multiplier

16位数的二进制乘法原理可以表示为以下的公式：
$\sum_{n=0}^{15} operand_A \times 2^n \times operand_B(n)$
根据这个公式就可以设计出array multiplier，即先移位再与前面的结果加起来，当B上的某一位为0的时候这一层加的数就是0，其结构如图fig15所示。在某一些处理器中，为了节约资源，乘法是需要借助加法器的协助的，并且不像这个结构一样在一个周期内就可以输出结果，而是通过多个周期的加法来计算结果，比如说在IBEX中就用了三种不同的方式来处理乘法，但这即种方式都是多周期累加。

fig15. array multiplier or carry save multiplier

对于乘法器还有一种适用于高速乘法运算的Booth乘法器，其基于booth算法。下面是booth 算法伪代码，由这个程序可知本来要相加M次的乘法现在只需要相加M/2次：

# 假设需要运行M bit的乘法： P=A*B
i=0 # 因数B的index
p=0 #乘积
while i<=M-2 loop # M为B的位数
	p=p+vp(B(i+1), B(i), B(i-1)) # vp的值由look up table查表得出，B（-1）=0
	A=A*4
	i=i+2
end loop

vp的look-up-table如下所示，也就是说我们在实现的时候可以用mux：

$y_{i+1}$	$y_i$	$y_{i-1}$	$V_p$
0	0	0	0
0	0	1	+A
0	1	0	+A
0	1	1	+2A
1	0	0	-2A
1	0	1	-A
1	1	0	-A
1	1	1	0

对于用于判断vp的值的B的内容运行情景如下：

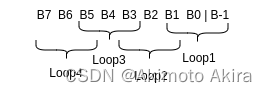
1.6 divider

除法器的原理是基于二进制短除法，下面的例子是 $1110_2 \div 11_2$ 的计算步骤：

step1: ${\color{red}11 \times 1=11}, {\color{green}11-11=00}$ ，这里的quatient为1，partial reminder为00
step2: $11 \times 0 > 001, 001-00=001$ ，所以这一步quatient为0，partial reminder为001
step3 $11 \times 0> 0010, 0010-00=0010$ ，所以这一步quatient为0，partial reminder为0010
step4 综上所述quatient为 $\times 2^0+0 \times 2^1 +1 \times 2^2 = 100$ ，reminder为10

由此可见每一阶段的除法的流程为：试商（红色）–> 乘上被除数并相减（绿色） --> 找到partial reminder （橙色），但是这里的难点是如何用硬件来实现试商的过程。就如上面写出的过程，我们可以将每一步求partial reminder的过程写成以下迭代公式，注意被除数必须大于除数：
$R^{j+1}=2\cdot R^j - q_{j+1}\cdot D$
其中：

R为partial reminder， $R^{0}$ 为被除数
r为进制中表示数的个数，这里是2进制只有{0,1}，所以r=2
q为每一步商的数字
D为除数

注意：这里的除数，商，余数和被除数都是看作放在小数点后面的！！！！用来计算的实际上是：
$Q=0.q1q2q2...\\ D=0.d1d2d3...\\ Z=R(0)=0.r1r2r3$

试商的过程表示如下：
$q_{j+1}=\left\{\begin{matrix} 0& if & 2\cdot R^j<D\\ 1& if & 2\cdot R^j\ge D \end{matrix}\right.$

下面是一个例子供大家理解过程：

A=0.01010110
B=0.1100

step1：
R(0)=0.01010110
判断2R(0)-B，因为其小于0，因此q(1)=0
step2:
R(1)=2R(0)-0B=0.1010110 在这一步2R(0)-B的值要存放在寄存器中用于下一次计算，实际上重复计算了上一个判断过程的操作，在non restoring divisor中优化
判断2R(1)-B，因为其大于0，因此q(2)=1
step3:(以此类推，直到partial reminder<=divisor为止)
q(3)=1
R(3)=0.01110
step4:
q(4)=1
R(4)=0.0010

因此最终商为0111余数为最后一个step的余数。上面的迭代步骤可以写成下面所示的伪代码：

while (partial reminder>divisor)
	assume q(j+1)=1
	R_ES(j+1)=2R(j)-B
		if R_ES>0
			q(j+1)=1
			R(j+1)=R_ES(j+1)
		else
			q(j+1)=0
			R(j+1)=R_ES(j+1)+B

除此之外为了提升执行效率还有另一个实现方法即non restoring除法器，这个方法中用于表示结果的有三种字符 $\{\overline{1}, 1, 0\}$ ，其中 $\overline{1}$ 相当于-1（redundant representation）。在进行结果转化的时候也是计算 $-1\cdot2^{k}$ 。与上面的方法不同的地方在于试商的过程和确定R(j+1)的过程，用这种方式实现则不需要存放reminder，因为 $2R^j$ 用一个移位寄存器就能实现而不需要特意再用另一个寄存器去存储余数的结果：

$R_{j+1}=\left\{\begin{matrix} 2R_{j}-D & if & 2R^j > 0\\ 2R_{j}+D& if & 2R^j < 0 \end{matrix}\right.$

$q_{j+1}=\left\{\begin{matrix} 1 & if & \frac{1}{2}\le 2R^j\\ -1& if & 2R^j <-\frac{1}{2} \end{matrix}\right.$

下面是non restoring divisor的电路实现，其中Reminder是一个移位寄存器，上面迭代的过程也是为除法为什么在流水线中需要多个周期才能完成的原因：

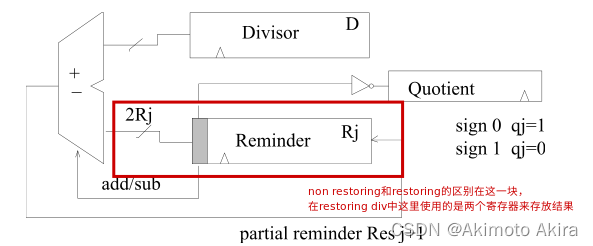
fig16 iterative non restoring divisor

在此基础上为了进一步简化操作提出SRT除法器，radix-2 SRT算法的数字集为{-1,0,1}，在二进制非恢复算法的数字集中加入了0，当从该数字集中选择0时，只需要进行简单的移位，不需要进行加法的步骤
$R_{j+1}=\left\{\begin{matrix} 2R_{j}-D & if & \frac{1}{2}\le 2R^j\\ 2R_{j} & if & -\frac{1}{2}\le 2R^j <\frac{1}{2}\\ 2R_{j}+D& if & 2R^j <-\frac{1}{2} \end{matrix}\right.$

$q_{j+1}=\left\{\begin{matrix} 1 & if & \frac{1}{2}\le 2R^j\\ 0 & if & -\frac{1}{2}\le 2R^j <\frac{1}{2}\\ -1& if & 2R^j <-\frac{1}{2} \end{matrix}\right.$

在SRT除法器中如若需要进一步缩减其运行时间，那么需要增加其radix，一般来说这个值会是 $2^k$ ，例如radix-4我们所用来表示商的字符数为[0, 1, 2, 3]再加上负数一边就是[-3, -2, -1, 0, 1, 2, 3]。但是这样做会导致商选择器变得更加复杂。

总结：

restoring div的数字集为{0,1}；
non restoring div的数字集为{-1,1}，相比于restoring div，不必进行“恢复”操作，加快了算法的迭代，提升了算法的性能；
SRT算法的数字集为{-1,0,1}，在non restoring div的数字集中加入了0，当从该数字集中选择0时，只需要进行简单的移位，不需要进行加法的步骤，简化了计算。

1.7 register file

寄存器堆实际上就是很多寄存器堆在一个元器件里，其外部端口如fig18所示：

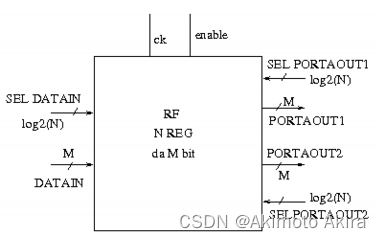
fig18 external ports of register file

最简单的寄存器堆就是将很多寄存器按照地址合在一起。但是在实际应用中根据应用场景的不同还有别样的寄存器堆设计。例如在子程序的额外开销比较多的情境下。register windowing技术可以减少register file和memory由于现场保护而产生的数据交换开销，在不同的子程序中就可以直接使用不同的window囊括进的register而不需要额外在memory中堆栈。
第一种windowing register file是 fixed windowing RF，其不同的窗口固定对应不同的寄存器组且窗口大小固定不变。另一类是flexible window，其窗口大小是可变的。在windowing register中，一个给子程序使用的寄存器窗口中的寄存器可以分为四类：

GL（global）：用于存放全局可用的数据，这部分窗口不会变
IN（input）：用于存放继承自parent routine的输入数据
LOC（local）：用于存放子程序自用的数据，
OUT（output）：用于存放子程序输出给子程序的子程序的结果数据

在嵌套子程序的时候IN，LOC，OUT会如fig19所示的路线移动，直到寄存器堆的空间用完后，还要继续调用子程序时才会将当前寄存器堆中最上层的程序放在寄存器里的数据堆栈到memory中然后重复上面的操作，在退出子程序时才会将堆栈释放重新将内容放入window框起来的寄存器中，在CPU运行时也只会看到window中的寄存器：

fig19 window register file

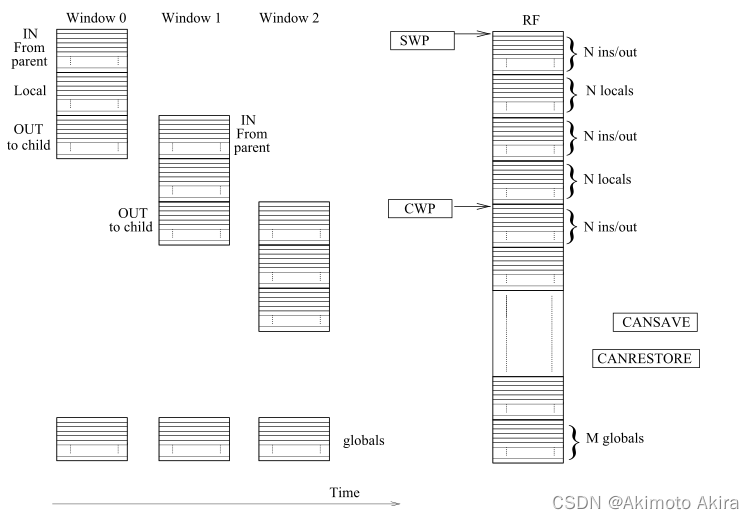
其实现我们可以用下面的方式来实现寄存器阵列，如果不是window register的话就不需要，直接用几个寄存器连上地址译码器就可以了：

subtype REG_ADDR is natural range 0 to 31; 						-- using natural type
type REG_ARRAY is array(REG_ADDR) of std_logic_vector(63 downto 0); 
signal REGISTERS : REG_ARRAY;

part2. Control unit设计

FSM一般来说用State diagram表示。FSM中需要的基本组成部件有：

state
iniput, output
initial state
transition
action

一个简单的例子：

library ieee;
use ieee.std_logic_1164.all

entity FSM is
port(clk: in std_logic;
	   rst: in std_logic;
	   a: in std_logic;
	   b:in std_logic;
	   o1: out std_logic;
	   o2: out std_logic);
end entity;

architecture beh of FSM is
	type fsm_state is (s0,s1,s2,s3,s4); #注意这个state的定义方法
	signal curr_state, next_state: fsm_state;
begin
	process(clk) #这个过程用clk驱动state的转换，这就是一个state register
	begin
		if (clk=1 and clk'event) then
			if (rst='1') then # synchronous, raising edge reset
				curr_state<=s0;
			else
				curr_state<=next_state;
			end if;
		end if;
	end process;
	
	process(curr_state) #注意这个一定是放在process中，因为这个不是一个RTL的描述
	begin
		case curr_state is
			when s0 =>
				next_state<=s1;
			when s1=>
				if ((a and b)=1) then
					next_state<=s2;
				else
					next_state<=3;
				end if;	
			when s2=>
				o1<='0';
				o2<='1';
				next_state<=s4;
			when s3=>
				o1<='1';
				o2<='0';	
				next_state<=s4			
			when s4=>
				next_state<=s0;
		end case
	end process;
end beh;

这里实现的FSM的state diagram为 fig20所示。

fig20 simple FSM example

FSM主要有两类，一类是Mealy另一类是Moore。Moore的输出只取决于当前的状态，其输入只用来控制状态转移。而Mealy的输入不仅用来控制状态还要用来控制当前的输出。Mealy通常比Moore更小，但是可能里面的电路不会完全同步。Moore通常会有更短的critical path。
对于CPU而言，其有两种方式输出所需要的控制字，一种是用FSM，通过通过判断当前的状态和opcode输出下一个状态和control word，这个方式下控制寄存器可以塞进这里；另一种是用look-up-table，在opcode和state flag（这个可以由外部输入）的输入提示下确定control word在LUT中的地址，并输出，这种称为hard-wired approach。

part3. CPU SoC上的其它部件 (TODO：理解总结)

3.1 总线

AMBA（parallel）

通常用于SoC上部件之间通信。在AMBA协议中主要包含3中不同的总线标准：AHB（advanced high performance bus），ASB（advanced system bus）， APB（advanced peripheral bus）。然而在specification中只有提到其有不同时钟上的特性，并不涉及各自的电气属性。一般而言AHB和ASB用于高速、高性能设备之间的通信，这两者的不同之处在于ASB缺少了一些在AHB有关高速传输的功能。当设备对这些功能没有要求时可以用ASB作为替代（Burst transfers, Split transactions），这两者主要用于处理器和on-chip memory之间的信息交换。APB则主要用于低速、低带宽、低功耗的外设之间的信息传递，例如GPIO，USART等，当这些外设要与CPU和memory进行数据交换时需要通过一个总线协议转换桥进行，即AHB2APB或ASB2APB bridge。通常SoC的架构如图fig-所示

fig-.通常情况下的SoC上部件和总线协议使用情况

AMBA需要矫正的一个概念是这是一个“协议”或者说这是一个“规格标准”，而不是一个实际的库，就跟RISCV一样，电气实现的方法是由设计者定义的，其中这个标准还有不同的版本AXI3，4，5等。（注：在实现总线协议时用有限状态机的模型去实现）这里提供一个usart协议发送逻辑的实现片段：

	...
	-- 发送状态定义
    type tx_state_type is (IDLE, START_BIT, DATA_BITS, STOP_BIT);
    signal tx_state     : tx_state_type := IDLE;
	...
	-- 发送逻辑
    process (clk)
    begin
        if rising_edge(clk) then
            if reset = '1' then
                tx_reg <= (others => '0');
                tx_state <= IDLE;
                tx_counter <= 0;
                tx <= '1';
                baud_counter <= 0;
            else
                case tx_state is
                    when IDLE =>
                        if tx_reg /= (others => '0') then
                            tx_state <= START_BIT;
                            tx_counter <= 0;
                            tx <= '0';
                            baud_counter <= 0;
                        end if;
                    when START_BIT =>
                        if baud_counter = CLK_FREQ/BAUD_RATE-1 then
                            tx <= '1';
                            tx_state <= DATA_BITS;
                            tx_counter <= 0;
                            baud_counter <= 0;
                        else
                            baud_counter <= baud_counter + 1;
                        end if;
                    when DATA_BITS =>
                        if baud_counter = CLK_FREQ/BAUD_RATE-1 then
                            tx <= tx_reg(tx_counter);
                            tx_counter <= tx_counter + 1;
                            if tx_counter = 8 then
                                tx_state <= STOP_BIT;
                            end if;
                            baud_counter <= 0;
                        else
                            baud_counter <= baud_counter + 1;
                        end if;
                    when STOP_BIT =>
                        if baud_counter = CLK_FREQ/BAUD_RATE-1 then
                            tx <= '1';
                            tx_state <= IDLE;
                            tx_counter <= 0;
                            tx_reg <= (others => '0');
                            baud_counter <= 0;
                        else
                            baud_counter <= baud_counter + 1;
                        end if;
                end case;
            end if;
        end if;
    end process;

3.2 Memory

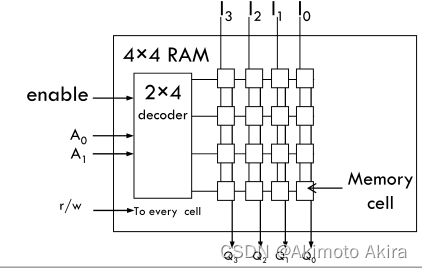
一个课读可写的memory的基本接口结构如图fig–所示。需要注意的是，内存的enable信号用于控制外部设备内存访问的权限，即当其未使能时，外部设备无法读写memory，但是此时内存的信息还是存在的，因此这个使能信号也可用于对内存数据的保护和与外部设备的读写操作同步。需要注意的是，根据其实现原理，memory本身是没有任何时序逻辑部件的，因此在读操作过程中，输入端输入地址的时候在输出端就会直接输出结果，没有任何延迟。内存读写的延迟实际上是由其memory cell的结构决定的。

fig2. 可读写memory基本接口和内部结构

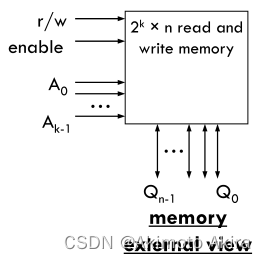
memory 的分级结构

从处理器开始到外存的顺序依次是：Register --> Cache --> Main memory （off chip memory）–> Disk（板载外存）。其存取速度是依次递减，单价也是递减，但是空间是依次增大的。
Cache一般是SRAM，其需要对main memory进行读写，同时处理器也要对cache中的内容进行检查，如果在其中有则标记为cache hit，处理器会直接在cache中调用；若没有则标记为cache miss，此是要去主存中调用。如果有分级缓存的话则是到相邻的下一级缓存中去调用，缓存中都没有找到的时候才去主存中调用。
cache和memory的管理有三个工作：

cache要如何与main memory中的地址对应
当cache中发生cache miss的时候，此时需要向主存申请数据。这是用于决定哪一个cache行需要被主存中的内容替换（这个是决定在CPU运行过程中命中率的关键算法）
当改变cache中的值时，是否要对主存中的原始数据进行更改或者做一些其它的工作用于标记这个数据的更改

cache和memory主要有三种不同的映射方式：Direct mapping, Fully associative mapping和Set associative mapping。