问题 A: 有重复元素的排列问题
题目描述
设R={ r 1 , r 2 , …, r n }是要进行排列的n个元素。其中元素r 1 , r 2 , …, r n 可能相同。试设计一个算法,
列出R的所有不同排列。给定n 以及待排列的n 个元素。计算出这n 个元素的所有不同排列。
输入
第1 行是元素个数n,1≤n≤500。接下来的1 行是待排列的n个元素。
输出
按字典序输出计算出的n个元素的所有不同排列,输出最后1行中的数是排列总数。
样例输入
4
aacc样例输出
aacc
acac
acca
caac
caca
ccaa
6嗯,next_permutation
记得要提前sort一下嗷
#include<bits/stdc++.h>
#define int long long
using namespace std;
char a[505];
char b[505];
int n;
vector<int>ans;
int num=1;
void fun(){
cout<<b<<endl;
while(next_permutation(b,b+n)){
printf("%s\n",b);
num++;
}
}
signed main(){
cin>>n;
scanf("%s",a);
sort(a,a+n);
strcpy(b,a);
fun();
cout<<num<<endl;
}
问题 B: 字符序列
题目描述
从三个元素的集合[A,B,C]中选取元素生成一个 N 个字符组成的序列,使得没有两个相邻字的子序列(子序列长度=2)相同。例:N = 5 时 ABCBA 是合格的,而序列 ABCBC与 ABABC 是不合格的,因为其中子序列 BC,AB 是相同的。
对于由键盘输入的 N(1<=N<=12),求出满足条件的 N 个字符的所有序列和其总数。
输入
4
输出
72
dfs咯,注意边界,dfs讨厌没有边界感的人!!!
那么,什么是边界呢?
当然就是长度大于等于n辣,还有嗷,长度大于等于3的时候,得判断符不符合条件才能push进去!不要随便就crush,dfs会抗拒的捏~
代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n;
int ans=0;
vector<int>a;
void dfs(){
if(a.size()>=n){
ans++;
return;
}
for(int i=1;i<=3;i++){
if(a.size()<3){
a.push_back(i);
}
else{
if(a[a.size()-1]==a[a.size()-3]&&a[a.size()-2]==i){
continue;
}
else{
a.push_back(i);
}
}
dfs();
a.pop_back();
}
}
signed main(){
cin>>n;
a.clear();
dfs();
cout<<ans<<endl;
}
问题 C: 自然数的拆分问题
题目描述
任何一个大于1的自然数n,总可以拆分成若干个小于n的自然数之和。
当n=7共14种拆分方法:
7=1+1+1+1+1+1+1
7=1+1+1+1+1+2
7=1+1+1+1+3
7=1+1+1+2+2
7=1+1+1+4
7=1+1+2+3
7=1+1+5
7=1+2+2+2
7=1+2+4
7=1+3+3
7=1+6
7=2+2+3
7=2+5
7=3+4
样例输入
7样例输出
1+1+1+1+1+1+1
1+1+1+1+1+2
1+1+1+1+3
1+1+1+2+2
1+1+1+4
1+1+2+3
1+1+5
1+2+2+2
1+2+4
1+3+3
1+6
2+2+3
2+5
3+4
提示
2=<n<=10
哈哈,和上一题很像捏,还是注意边界感就行辣
边界是什么?
和等于n就输出,和大于n直接return
注意咯,是个递增序列!所以我们不是从1开始,而是从t开始
t是什么?
哈哈,我也说不清,自己悟吧哈哈哈
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n;
vector<int>a;
int num;
void dfs(int t){
if(num==n){
cout<<a[0];
for(int i=1;i<a.size();i++){
cout<<"+"<<a[i];
}
cout<<endl;
return ;
}
else if(num>n){
return ;
}
for(int i=t;i<n;i++){
a.push_back(i);
num+=i;
dfs(i);
num-=i;
a.pop_back();
}
}
signed main(){
cin>>n;
dfs(1);
}
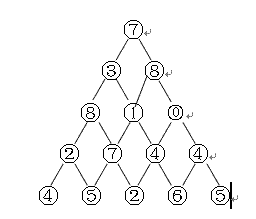
问题 D: 数字三角形问题,《算法入门经典》P259,动态规划,刘丽萍,CCF六级
题目描述
下图给出了一个数字三角形,请编写一个程序,计算从顶至底的某处的一条路径,使该路径所经过的数字的总和最大。
(1)每一步可沿左斜线向下或右斜线向下
(2)1 < 三角形行数 < 100
(3)三角形数字为0,1,…99
输入
有很多个测试案例,对于每一个测试案例, 通过键盘逐行输入,第1行是输入整数(如果该整数是0,就表示结束,不需要再处理),表示三角形行数n,然后是n行数
输出
输出最大值。
样例输入
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5样例输出
30呼呼,这是一个隐藏的动态规划,找到转移方程就好啦
转移方程是什么?
当然是:dp[i][j]=a[i][j]+max(dp[i-1][j],dp[i-1][j-1]);
然后就没了。。。
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n;
int a[105][105];
int dp[105][105];
void fun(){
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
dp[i][j]=a[i][j]+max(dp[i-1][j],dp[i-1][j-1]);
}
}
int max=0;
for(int i=1;i<=n;i++){
if(max<dp[n][i]){
max=dp[n][i];
}
}
cout<<max<<endl;
}
signed main(){
while(cin>>n){
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
cin>>a[i][j];
}
}
fun();
}
}
问题 E: 最大间隙问题
题目描述
给定n个实数X1,X2,X3...Xn,求这n个数在实轴上相邻两个数之间的最大差值。
输入
输入有两行,第一行为n(0<n<=300000),第二行为n个实数,实数范围在-100000000-100000000
输出
输出为两个相邻实数间的最大差值
样例输入
5
2.3 3.1 7.5 1.5 6.3
样例输出
3.2呼呼,这里偷鸡,直接用set,哈哈哈,我记着正规写法是分治来着?
忘了,管他呢,能过就行,呼呼
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n;
set<double>a;
signed main(){
cin>>n;
for(int i=0;i<n;i++){
double temp=0;
scanf("%lf",&temp);
a.insert(temp);
}
double ans=0;
auto it = a.begin();
auto pre=it;
it++;
for(;it != a.end();it++){
double num=*it - *pre;
if(num>ans){
ans=num;
}
pre=it;
}
cout<<ans<<endl;
}