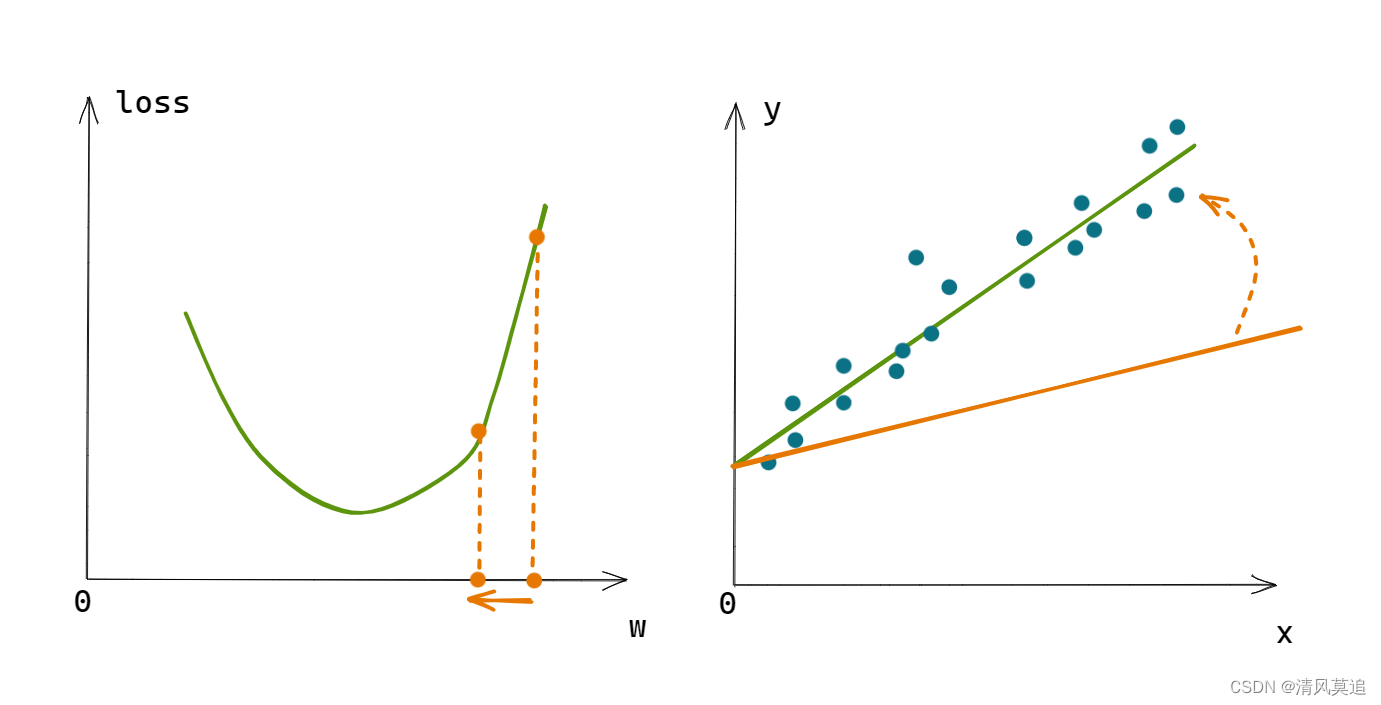目录
- 0 写在前面
- 1 流形学习
- 2 局部线性嵌入算法
- 2.1 什么是局部线性嵌入?
- 2.2 算法原理推导
- 3 Python实现
- 3.1 算法流程
- 3.2 核心代码
- 3.3 可视化
0 写在前面
机器学习强基计划聚焦深度和广度,加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理;“广”在分析多个机器学习模型:决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。强基计划实现从理论到实践的全面覆盖,由本人亲自从底层编写、测试与文章配套的各个经典算法,不依赖于现有库,可以大大加深对算法的理解。
🚀详情:机器学习强基计划(附几十种经典模型源码)
1 流形学习
在机器学习强基计划8-4:流形学习等度量映射Isomap算法(附Python实现)中,我们介绍了流形(manifolds)的概念,它是可以局部欧几里得空间化的一个拓扑空间,是具有拓扑结构的点集,是欧几里得空间中的曲线、曲面等概念的推广。对流形的物理意义不熟悉的同学可以回顾上一篇文章。

流形学习(manifold learning)是基于流形的机器学习算法,它假设样本数据分布在高维特征空间中的低维嵌入流形上,虽然整体十分复杂,但局部上仍具有欧氏空间的性质,因此可以在局部建立降维映射关系,然后再将局部映射关系推广到全局——局部线性构造全局非线性。流形学习旨在从观测样本中去寻找产生数据分布的内在本质规律,而非破坏结构性地降维。
2 局部线性嵌入算法
2.1 什么是局部线性嵌入?
局部线性嵌入(Locally Linear Embedding, LLE)限制样本在降维后的低维空间中的 k k k近邻局部线性关系,等价于原始空间。
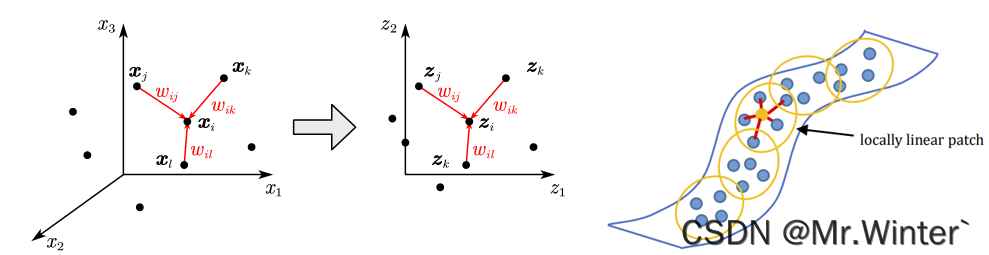
例如,若高维样本满足 x i = w i j x j + w i k x k + w i l x l \boldsymbol{x}_i=w_{ij}\boldsymbol{x}_j+w_{ik}\boldsymbol{x}_k+w_{il}\boldsymbol{x}_l xi=wijxj+wikxk+wilxl,则低维样本同样满足 z i = w i j z j + w i k z k + w i l z l \boldsymbol{z}_i=w_{ij}\boldsymbol{z}_j+w_{ik}\boldsymbol{z}_k+w_{il}\boldsymbol{z}_l zi=wijzj+wikzk+wilzl,如图所示,其中 w i \boldsymbol{w}_i wi称为样本 x i \boldsymbol{x}_i xi的重构系数。
2.2 算法原理推导
设高维样本 x i \boldsymbol{x}_i xi的 k k k近邻样本集合为 Q i k Q_{i}^{k} Qik,则重构系数应满足
min w 1 , w 2 , ⋯ , w m ∑ i = 1 m ∥ x i − ∑ j ∈ Q i k w i j x j ∥ 2 2 s . t . ∑ j ∈ Q i k w i j = 1 ( i = 1 , 2 , ⋯ , m ) \underset{\boldsymbol{w}_1,\boldsymbol{w}_2,\cdots ,\boldsymbol{w}_m}{\min}\sum_{i=1}^m{\left\| \boldsymbol{x}_i-\sum_{j\in Q_{i}^{k}}{w_{ij}\boldsymbol{x}_j} \right\| _{2}^{2}}\,\, \mathrm{s}.\mathrm{t}. \sum_{j\in Q_{i}^{k}}{w_{ij}}=1\left( i=1,2,\cdots ,m \right) w1,w2,⋯,wmmini=1∑m xi−j∈Qik∑wijxj 22s.t.j∈Qik∑wij=1(i=1,2,⋯,m)
为便于优化,将其改写为矩阵形式
min w 1 , w 2 , ⋯ , w m ∑ i = 1 m w i T X ~ i T X ~ i w i s . t . w i T 1 k × 1 = 1 ( i = 1 , 2 , ⋯ , m ) \underset{\boldsymbol{w}_1,\boldsymbol{w}_2,\cdots ,\boldsymbol{w}_m}{\min}\sum_{i=1}^m{\boldsymbol{w}_{i}^{T}\boldsymbol{\tilde{X}}_{i}^{T}\boldsymbol{\tilde{X}}_i\boldsymbol{w}_i}\,\, \mathrm{s}.\mathrm{t}. \boldsymbol{w}_{i}^{T}\mathbf{1}_{k\times 1}=1\left( i=1,2,\cdots ,m \right) w1,w2,⋯,wmmini=1∑mwiTX~iTX~iwis.t.wiT1k×1=1(i=1,2,⋯,m)
其中 w i = [ w i 1 w i 2 ⋯ w i k ] T \boldsymbol{w}_i=\left[ \begin{matrix} w_{i1}& w_{i2}& \cdots& w_{ik}\\\end{matrix} \right] ^T wi=[wi1wi2⋯wik]T, X ~ i = [ x i − x j 1 x i − x j 2 ⋯ x i − x j k ] , j ∈ Q i k \boldsymbol{\tilde{X}}_i=\left[ \begin{matrix} \boldsymbol{x}_i-\boldsymbol{x}_{j_1}& \boldsymbol{x}_i-\boldsymbol{x}_{j_2}& \cdots& \boldsymbol{x}_i-\boldsymbol{x}_{j_k}\\\end{matrix} \right] , j\in Q_{i}^{k} X~i=[xi−xj1xi−xj2⋯xi−xjk],j∈Qik,应用拉格朗日乘子法可得
L ( w 1 , w 2 , ⋯ , w m , λ ) = ∑ i = 1 m w i T X ~ i T X ~ i w i + λ ( w i T 1 k × 1 − 1 ) L\left( \boldsymbol{w}_1,\boldsymbol{w}_2,\cdots ,\boldsymbol{w}_m,\lambda \right) =\sum_{i=1}^m{\boldsymbol{w}_{i}^{T}\boldsymbol{\tilde{X}}_{i}^{T}\boldsymbol{\tilde{X}}_i\boldsymbol{w}_i}+\lambda \left( \boldsymbol{w}_{i}^{T}\mathbf{1}_{k\times 1}-1 \right) L(w1,w2,⋯,wm,λ)=i=1∑mwiTX~iTX~iwi+λ(wiT1k×1−1)
对 w i \boldsymbol{w}_i wi求梯度,并令之为0可得
∇ w i L ( w 1 , w 2 , ⋯ , w m , λ ) = w i T X ~ i T X ~ i w i + λ ( w i T 1 k × 1 − 1 ) = 2 X ~ i T X ~ i w i + λ 1 k × 1 = 0 ⇒ w i = − 1 2 λ ( X ~ i T X ~ i ) − 1 1 k × 1 \begin{aligned}\nabla _{\boldsymbol{w}_i}L\left( \boldsymbol{w}_1,\boldsymbol{w}_2,\cdots ,\boldsymbol{w}_m,\lambda \right) &=\boldsymbol{w}_{i}^{T}\boldsymbol{\tilde{X}}_{i}^{T}\boldsymbol{\tilde{X}}_i\boldsymbol{w}_i+\lambda \left( \boldsymbol{w}_{i}^{T}\mathbf{1}_{k\times 1}-1 \right) \\&=2\boldsymbol{\tilde{X}}_{i}^{T}\boldsymbol{\tilde{X}}_i\boldsymbol{w}_i+\lambda \mathbf{1}_{k\times 1}\\&=0\\\Rightarrow \,\, \boldsymbol{w}_i&=-\frac{1}{2}\lambda \left( \boldsymbol{\tilde{X}}_{i}^{T}\boldsymbol{\tilde{X}}_i \right) ^{-1}\mathbf{1}_{k\times 1}\end{aligned} ∇wiL(w1,w2,⋯,wm,λ)⇒wi=wiTX~iTX~iwi+λ(wiT1k×1−1)=2X~iTX~iwi+λ1k×1=0=−21λ(X~iTX~i)−11k×1
考虑到 w i T 1 k × 1 = 1 k × 1 T w i = 1 \boldsymbol{w}_{i}^{T}\mathbf{1}_{k\times 1}=\mathbf{1}_{k\times 1}^{T}\boldsymbol{w}_i=1 wiT1k×1=1k×1Twi=1,两边同时左乘 1 k × 1 T \mathbf{1}_{k\times 1}^{T} 1k×1T可得
− 1 2 λ = 1 1 k × 1 T ( X ~ i T X ~ i ) − 1 1 k × 1 -\frac{1}{2}\lambda =\frac{1}{\mathbf{1}_{k\times 1}^{T}\left( \boldsymbol{\tilde{X}}_{i}^{T}\boldsymbol{\tilde{X}}_i \right) ^{-1}\mathbf{1}_{k\times 1}} −21λ=1k×1T(X~iTX~i)−11k×11
联立消去 λ \lambda λ可得
w i = ( X ~ i T X ~ i ) − 1 1 k × 1 1 k × 1 T ( X ~ i T X ~ i ) − 1 1 k × 1 \boldsymbol{w}_i=\frac{\left( \boldsymbol{\tilde{X}}_{i}^{T}\boldsymbol{\tilde{X}}_i \right) ^{-1}\mathbf{1}_{k\times 1}}{\mathbf{1}_{k\times 1}^{T}\left( \boldsymbol{\tilde{X}}_{i}^{T}\boldsymbol{\tilde{X}}_i \right) ^{-1}\mathbf{1}_{k\times 1}} wi=1k×1T(X~iTX~i)−11k×1(X~iTX~i)−11k×1
在低维空间中需要维护这组 w i ( i = 1 , 2 , ⋯ , m ) ∈ R k × 1 \boldsymbol{w}_i\left( i=1,2,\cdots ,m \right) \in \mathbb{R} ^{k\times 1} wi(i=1,2,⋯,m)∈Rk×1,因此优化目标为
min z 1 , z 2 , ⋯ , z m ∑ i = 1 m ∥ z i − ∑ j ∈ Q i k w i j z j ∥ 2 2 s . t . ∑ i z i = 0 , 1 m − 1 ∑ i z i z i T = I \underset{\boldsymbol{z}_1,\boldsymbol{z}_2,\cdots ,\boldsymbol{z}_m}{\min}\sum_{i=1}^m{\left\| \boldsymbol{z}_i-\sum_{j\in Q_{i}^{k}}{w_{ij}\boldsymbol{z}_j} \right\| _{2}^{2}}\,\, \mathrm{s}.\mathrm{t}. \sum_i{\boldsymbol{z}_i}=0, \frac{1}{m-1}\sum_i{\boldsymbol{z}_i}\boldsymbol{z}_{i}^{T}=\boldsymbol{I} z1,z2,⋯,zmmini=1∑m zi−j∈Qik∑wijzj 22s.t.i∑zi=0,m−11i∑ziziT=I
将重构向量增广为 w ~ i ∈ R m × 1 \boldsymbol{\tilde{w}}_i\in \mathbb{R} ^{m\times 1} w~i∈Rm×1,多余的位置为0;约束条件表示了降维样本的分布模式——样本中心化去除平移自由度、样本单位协方差去除缩放自由度。
将优化目标改为矩阵形式
min Z ∑ i = 1 m ∥ Z i i − Z w ~ i ∥ 2 2 = min Z ∑ i = 1 m ( Z ( i i − w ~ i ) ) T Z ( i i − w ~ i ) = min Z t r ( Z ( I − W ~ ) ( Z ( I − W ~ ) ) T ) = min Z t r ( Z M Z T ) s . t . Z Z T = ( m − 1 ) I \begin{aligned}\underset{\boldsymbol{Z}}{\min}\sum_{i=1}^m{\left\| \boldsymbol{Zi}_i-\boldsymbol{Z\tilde{w}}_i \right\| _{2}^{2}}&=\underset{\boldsymbol{Z}}{\min}\sum_{i=1}^m{\left( \boldsymbol{Z}\left( \boldsymbol{i}_i-\boldsymbol{\tilde{w}}_i \right) \right) ^T\boldsymbol{Z}\left( \boldsymbol{i}_i-\boldsymbol{\tilde{w}}_i \right)}\\&=\underset{\boldsymbol{Z}}{\min}\,\,\mathrm{tr}\left( \boldsymbol{Z}\left( \boldsymbol{I}-\boldsymbol{\tilde{W}} \right) \left( \boldsymbol{Z}\left( \boldsymbol{I}-\boldsymbol{\tilde{W}} \right) \right) ^T \right) \\&=\underset{\boldsymbol{Z}}{\min}\,\,\mathrm{tr}\left( \boldsymbol{ZMZ}^T \right) \,\, \\\mathrm{s}.\mathrm{t}. \boldsymbol{ZZ}^T&=\left( m-1 \right) I\end{aligned} Zmini=1∑m∥Zii−Zw~i∥22s.t.ZZT=Zmini=1∑m(Z(ii−w~i))TZ(ii−w~i)=Zmintr(Z(I−W~)(Z(I−W~))T)=Zmintr(ZMZT)=(m−1)I
采用拉格朗日乘子法
L ( Z , Λ ) = t r ( Z M Z T ) + t r ( Λ T ( Z Z T − ( m − 1 ) I ) ) L\left( \boldsymbol{Z},\boldsymbol{\varLambda } \right) =\mathrm{tr}\left( \boldsymbol{ZMZ}^T \right) +\mathrm{tr}\left( \boldsymbol{\varLambda }^T\left( \boldsymbol{ZZ}^T-\left( m-1 \right) \boldsymbol{I} \right) \right) L(Z,Λ)=tr(ZMZT)+tr(ΛT(ZZT−(m−1)I))
令 ∂ L ( Z , Λ ) / ∂ Z = 2 Z M + 2 Λ Z = 0 {{\partial L\left( \boldsymbol{Z},\boldsymbol{\varLambda } \right)}/{\partial \boldsymbol{Z}}}=2\boldsymbol{ZM}+2\boldsymbol{\varLambda Z}=0 ∂L(Z,Λ)/∂Z=2ZM+2ΛZ=0,移项转置可得 M Z T = − Z T Λ \boldsymbol{MZ}^T=-\boldsymbol{Z}^T\boldsymbol{\varLambda } MZT=−ZTΛ。设 Y = Z T ∈ R m × d \boldsymbol{Y}=\boldsymbol{Z}^T\in \mathbb{R} ^{m\times d} Y=ZT∈Rm×d,则有 M Y = − Y Λ \boldsymbol{MY}=-\boldsymbol{Y\varLambda } MY=−YΛ,这与主成分分析类似,只需对 M \boldsymbol{M} M特征值分解,并取 d ′ ≪ d d'\ll d d′≪d个最小特征值对应的特征向量构成 Y ∗ ∈ R m × d ′ \boldsymbol{Y}^*\in \mathbb{R} ^{m\times d'} Y∗∈Rm×d′,转置后即得低维样本 Z ∗ ∈ R d ′ × m \boldsymbol{Z}^*\in \mathbb{R} ^{d'\times m} Z∗∈Rd′×m
必须指出, M \boldsymbol{M} M最小的特征值往往接近0,原因是根据权重和为一 W ~ T 1 = 1 \boldsymbol{\tilde{W}}^T\mathbf{1}=\mathbf{1} W~T1=1可得 ( I − W ~ T ) 1 = ( I − W ~ ) T 1 = 0 \left( \boldsymbol{I}-\boldsymbol{\tilde{W}}^T \right) \mathbf{1}=\left( \boldsymbol{I}-\boldsymbol{\tilde{W}} \right) ^T\mathbf{1}=\mathbf{0} (I−W~T)1=(I−W~)T1=0,两边同时左乘 ( I − W ~ ) \left( \boldsymbol{I}-\boldsymbol{\tilde{W}} \right) (I−W~)有 M 1 = 0 \boldsymbol{M}\mathbf{1}=\mathbf{0} M1=0,即此时特征向量为全1向量,无法反应数据特征,所以实际应用中会选取第 2 d ′ + 1 2~d'+1 2 d′+1个最小特征值对应的特征向量。
3 Python实现
3.1 算法流程
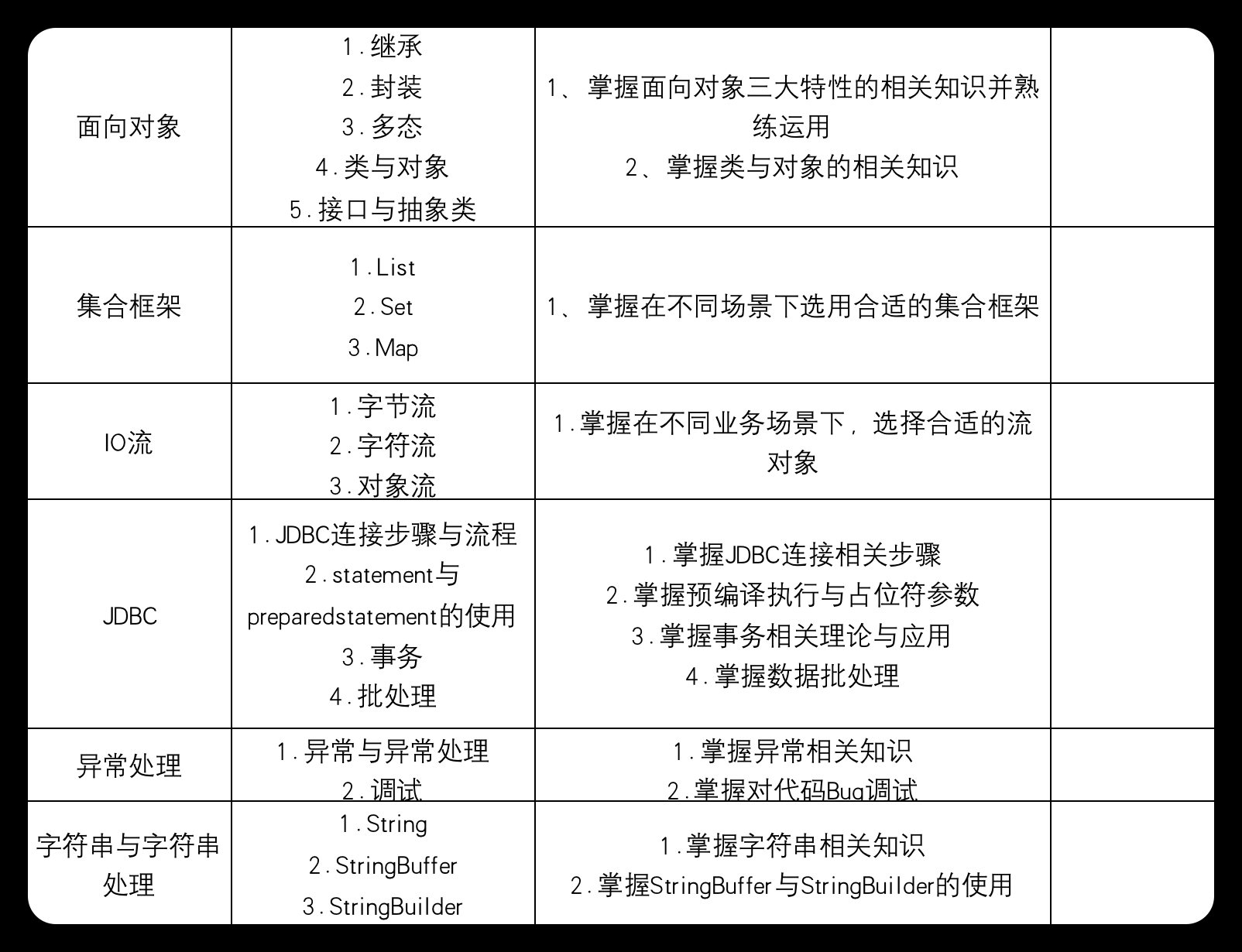
LLE算法流程如表所示,原理与第二节一一对应,不熟悉的同学可以往上翻

3.2 核心代码
LLE核心代码实现如下
def run(self, outDim):
# 获得距离矩阵
D = self.calDist()
D[D < 0] = 0
# 获得样本近邻索引矩阵
DIndex = np.argsort(D, axis=1)[:, 1:self.k + 1]
# 重构系数矩阵
W = np.zeros([self.m, self.m])
# 全1向量 kx1
unitK = np.ones([self.k, 1])
# 根据近邻样本确定重构参数
for i in range(self.m):
# Xi近邻距离矩阵
Xi = self.X[:, i].reshape(self.d, 1) - self.X[:, DIndex[i, :]]
# 求逆,附加项防止矩阵不稳定
XiInv = np.linalg.pinv(np.dot(Xi.T, Xi) + np.eye(self.k) * self.tol)
wi = np.dot(XiInv, unitK) / np.dot(np.dot(unitK.T , XiInv), unitK)
for j in range(self.k):
W[DIndex[i, j], i] = wi[j]
# 计算M矩阵
M = np.dot((np.eye(self.m) - W), (np.eye(self.m) - W).T)
# 特征值分解
eigVal, eigVec = np.linalg.eig(M)
# 获取最小的d'个特征值对应的索引
index = np.argsort(np.abs(eigVal))[1:outDim + 1]
eigVec_ = eigVec[:, index]
# 计算低维样本
Z = eigVec_.T
return Z
3.3 可视化
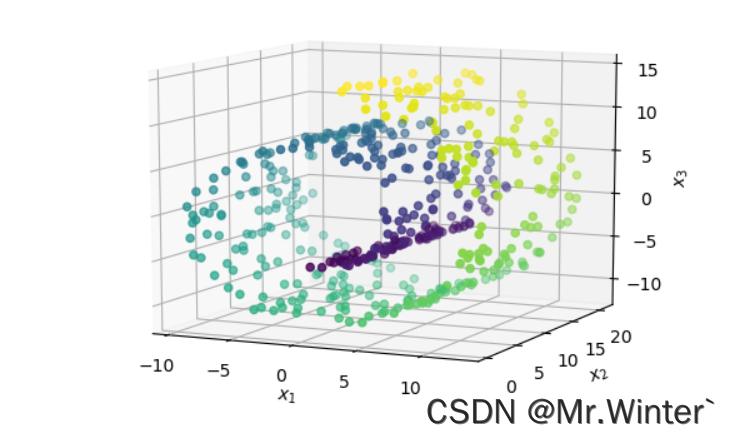
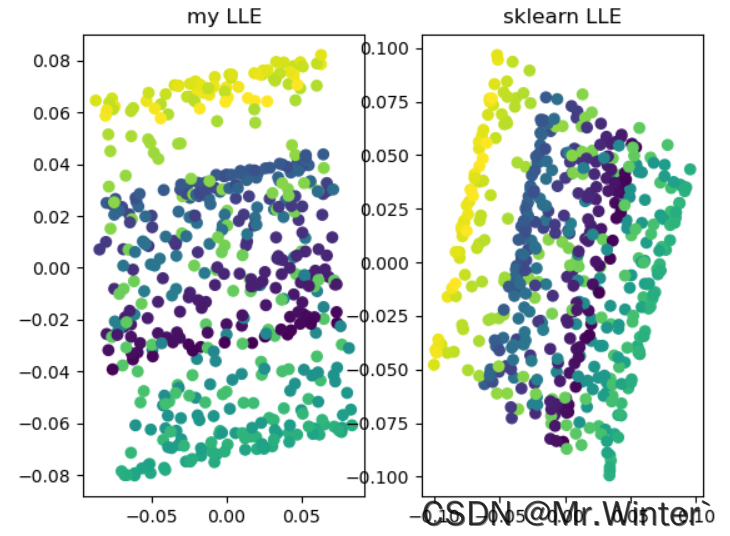
本文完整工程代码请通过下方名片联系博主获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …