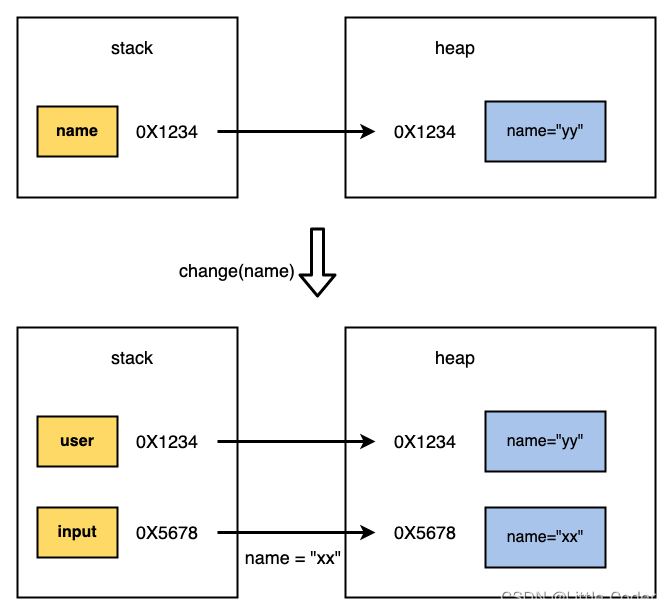
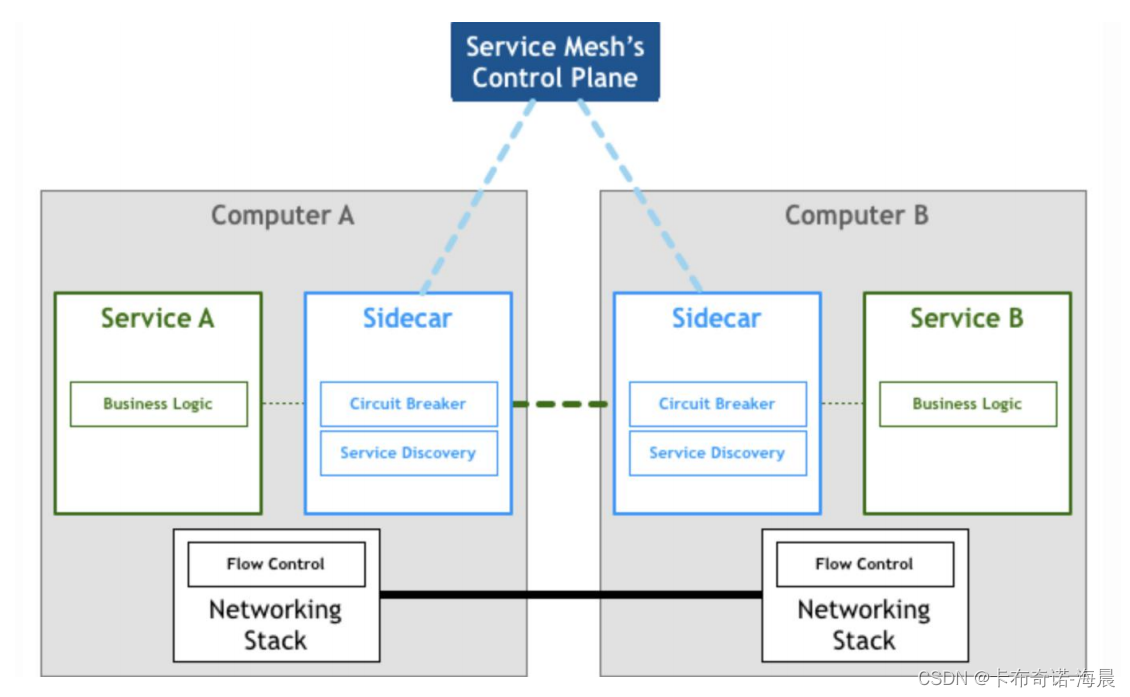
屏幕截图，是方便常用的功能。例如从网页或者视频中截图。但是有时候想去除截图中的背景颜色，怎么办？下面这个案例介绍如何去掉截图中的蓝色背景色。

这个小工具就能帮你方便实现。Web端的便捷小工具链接: http://www.artvily.com/renderCase?sample=toolLoader&demo=pngtoy

如何使用呢？下图是一张截图，要去除这张截图的蓝色背景：

打开上面所说的小工具网页，正常打开小工具之后，按下Ctrl+V快捷键复制已截图的内容到小工具，如下图所示：

此小工具试用版默认去除黑色背景，这里的需求是去除蓝色背景，所以点击 >> 按钮，展开高级功能。如下图所示：

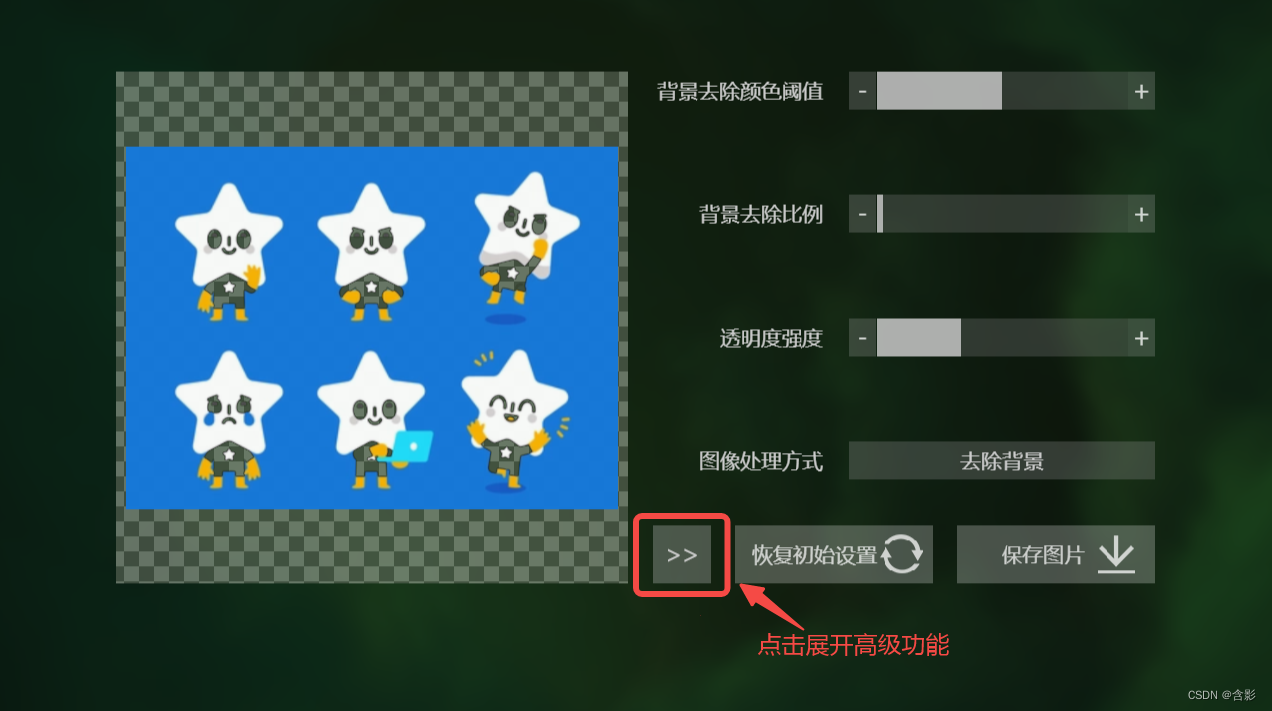
此小工具默认剔除黑色背景。其他颜色背景请点击展开高级功能。点击上图所示 >> 按钮展开高级功能。如下图所示：

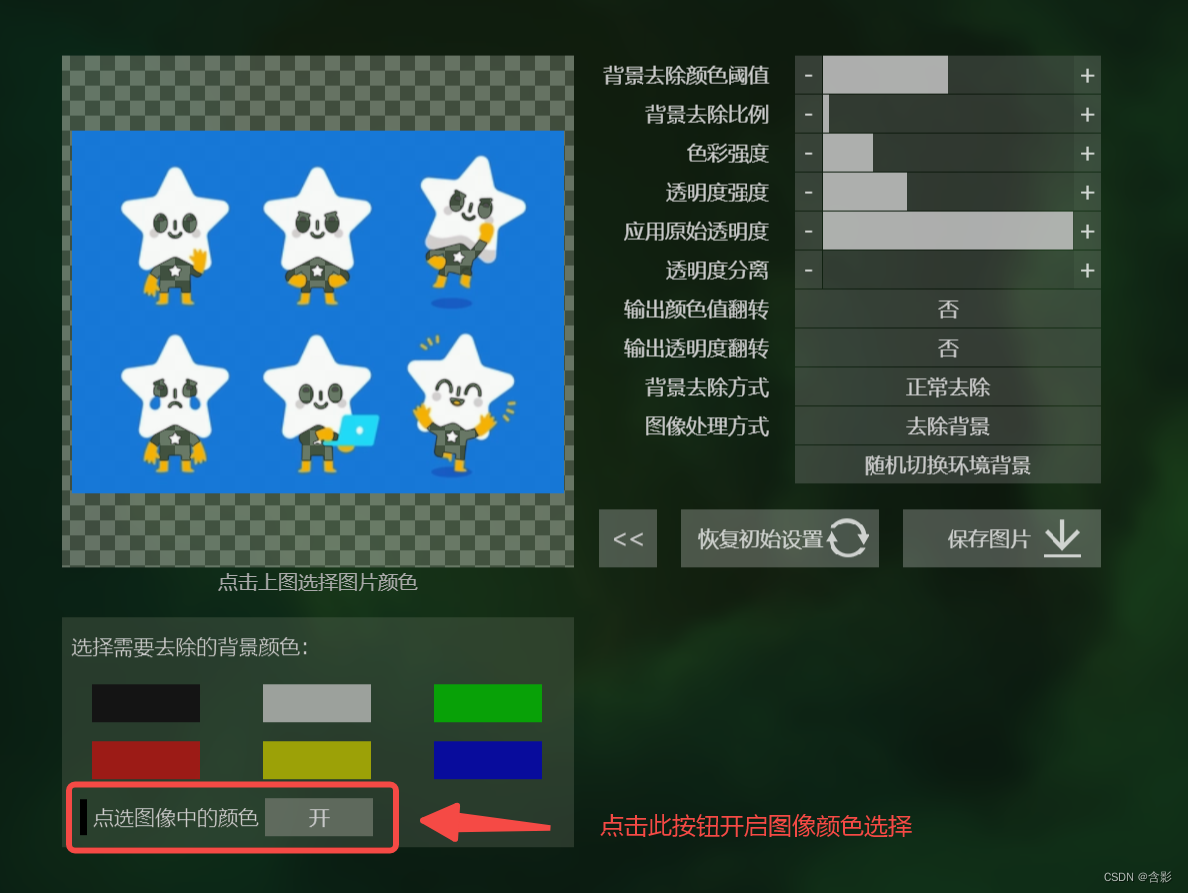
 开启颜色选择之后，直接用鼠标在图像的蓝色区域点击，就可去除蓝色背景。如下图所示：

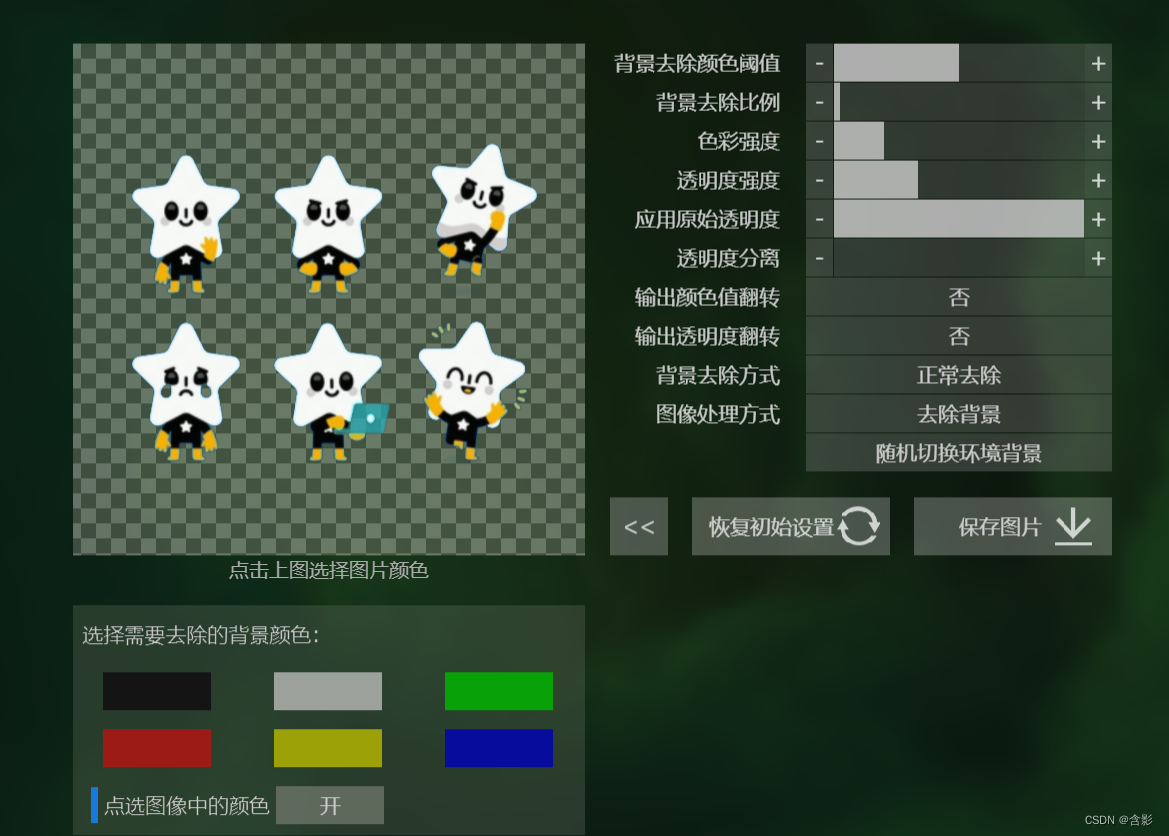
windwos下按下CTRL + S 快捷键保存或者点击保存图片按钮，处理后的截图图片效果如下

去除蓝色背景之后的图片效果如下：

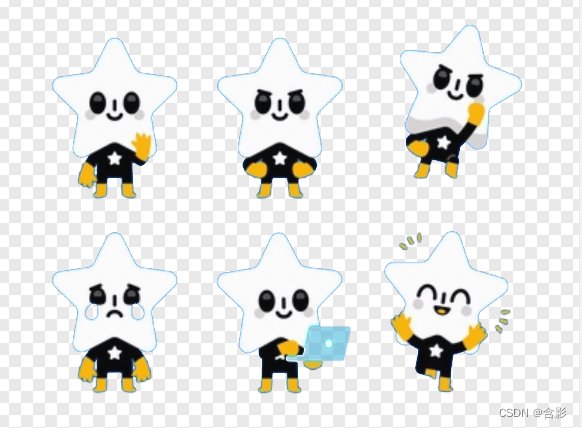
可以尝试调整更多操作，以便获得满意的效果。

 更多信息请见: 一个快速去除黑背景和其他颜色背景，生成透明PNG图的小工具_含影的博客-CSDN博客

是不是可以帮到你？

如果想快速打开图片文件，windows环境下可以按下 Ctrl + O 快捷键。