文章目录
- B树的定义和性质
- 为什么需要B树
- B树的定义
- B树的模拟实现
- 节点的数据结构
- B树的插入
- B树的删除
- B树的模拟实现
B树的定义和性质
我们之前已经对 平衡搜索二叉树有了一定的了解,学习了两种树——AVL树 和 红黑树,下面介绍一下B树
为什么需要B树
数据库中使用的就是B+树(和B树原理是一样的后面会单独介绍),那我们为什么不使用的AVL树和红黑树作为数据库的索引呢 ?原因是每次查询都是一次磁盘IO(数据库中的数据是存在file system中,每次查询的时候是需要读到内存中的),而磁盘IO中耗时最长的就是将磁盘读写磁头的定位,而每次查询都大概率都会移动磁头。所以如何降低IO的次数(实际上就是降低树的高度),就是降低总体查询时间。B树就是再次基础上做出了两点改进:
- 增加了没给节点的关键字数量——原先每个节点都是存储一个关键字,B树的每个节点存储M个关键字,这些关键字始终维护成一个有序的递增数列
- 把二叉树改成多叉树
这样一个树的高度就被压缩了很多,单次查询某个关键字所需要io的次数也变少了
B树的定义
首先我们要了解一下B树的度:即每个B树节点最多可以有M个子节点,这个M就是B树的度
- 每个结点的值(索引) 都是按递增次序排列存放的,并遵循左小右大原则。
- 对于所有节点来说:
关键字的数量始终=子节点的数量-1(这一点不论B树什么时候都必须满足)
- 对于根节点:
-关键字的数量满足[1,M-1]
- 子节点的数量满足[2,M]
- 对于除了根节点以外的其他节点
-关键字的数量满足[Math.ceil(M/2) , M-1] //Math.ceil代表向上取整
- 子节点的数量满足[Math.ceil(M/2) , M] //Math.ceil代表向上取整
- B树所有叶子节点位于同一层
我们下面都以度为3的B树作为样例作为讨论:
那么度为3的B树的节点吗,满足什么特性呢?
- 除了根节点以外的其他节点满足:
- 关键字个数:[1,2]
- 子节点的个数:[2,3]
- 根节点:
- 关键字的个数:[1,2]
- 子节点的个数:[2,3]
对于度为3的B树根节点和非根节点的要求是一样的,但是当度M>=5时候就会不一样了,读者可以自己计算一下。
B树的模拟实现
以下所有的都是以度为3的B树为示例
然后我们用less_key_number表示一个节点关键字最少的数量,这里为ceil(3/2)-1=1
注意:less+key_number的数量始终小于M/2——这里M/2不取整
节点的数据结构
节点数据结构的伪代码:
int cur_sz=0; //记录当前key的数量
K array_k[M]; //Key的数组
BTreeNode<K, M>* array_node[M+1]; // 存储子节点的数组
这里我们把关键字数组和子节点数组都多开了一个值,实际上还是符合上面B树的规则,只是方便后面插入时候将插入和调整过程分离
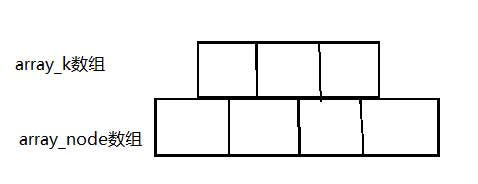
注意
- 我们把与array_k下标相等array_node叫做关键字array_k的左节点
- 我们把比array_k下标大一的array_node叫做关键字array_k的右节点
例如下标为i的array_k[i]的左节点为:array_node[i]右节点为:array_node[i-1]
B树的插入
插入过程的思路

注意: 我们在插入之前B树的所有节点的关键字都是满足数量的要求的,这是插入的前提
-
假设我们现在有一个节点如下:现在我们想要插入关键字9
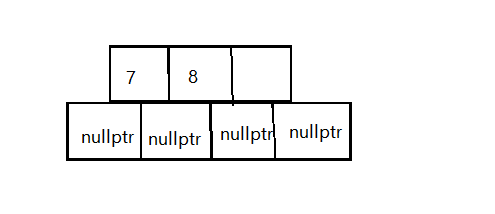
-
按照上面的思路先插入
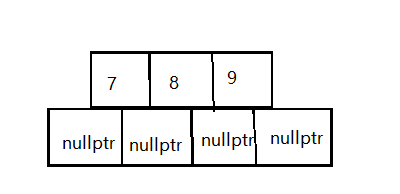
-
判断发现不满足B树的节点的关键字数量这时候我们就要进行分裂操作:
- 首先把该节点分成三部分,三部分关键字的数量为:
less_key_number+1+M-1-less_key_number,(这三部分我们后面分别用部分1、部分2、部分3代称)如果大伙感兴趣可以计算一下上面三个部分每个部分的关键字数量都不超过M/2(不论M是奇数还是偶数)。 - 把部分1和部分3分别分裂成两个新节点,部分2 作为关键字插入该节点的父节点
注意- 部分1和部分3分家的时候,我们把原节点当做部分1,创立一个新节点当做部分3,新节点部分三的
array_node和array_k都要从部分1中拷贝 - 部分2插入父节点,首先需要找到部分二在
array_k数组中的插入下标,而新分裂出来的两个子节点(部分1和部分3)就是部分2在父节点插入位置的左右子节点 - 父节点插入部分2的时候涉及到数组的移动,注意
array_k和array_node两个数组都需要相应的移动(这里的例子看不出来,下面会举一个相应的例子) - 如果像这个例子一样没有父节点或者说该节点就是根节点,那么需要创立一个父节点节点,并更新根节点
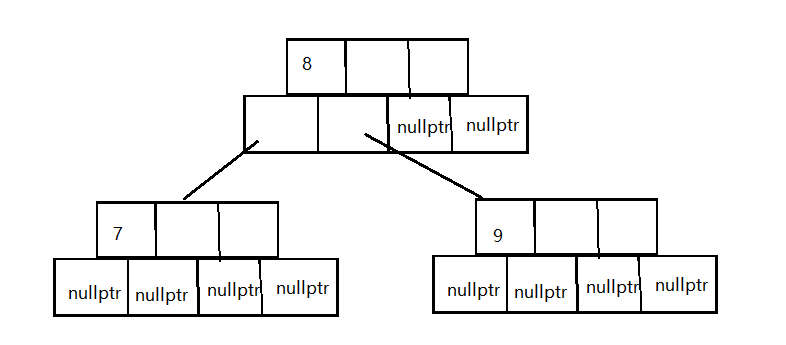
- 部分1和部分3分家的时候,我们把原节点当做部分1,创立一个新节点当做部分3,新节点部分三的
- 首先把该节点分成三部分,三部分关键字的数量为:
-
因为父节点中插入了一个新的关键字,可能导致父节点的关键字数量超出M-1所以需要继续向上遍历判断
ok这个最简单的例子看完了我们来看一个复杂一点的例子:
假设我们现在有了一个如下的B树👇,现在我们要插入关键字:3
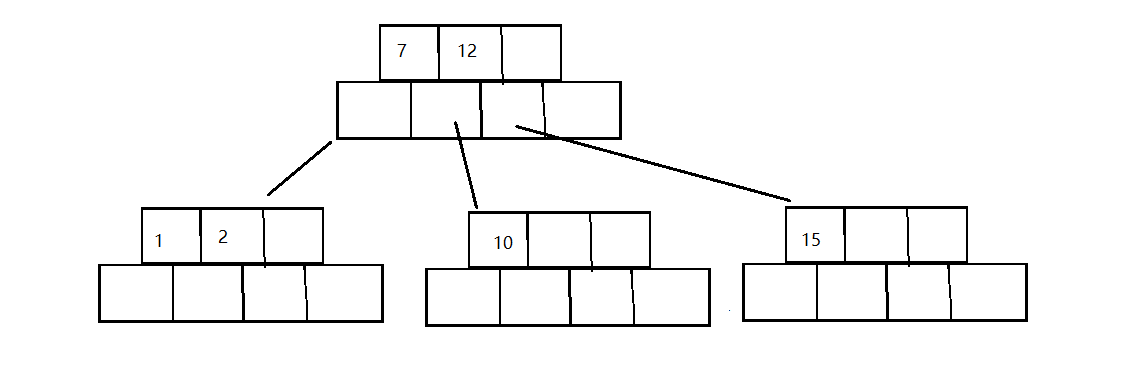
-
首先找到关键字3应该在哪个节点插入——很简单按照二叉搜索树去找(这里就不细说了)
-
找到后直接插入
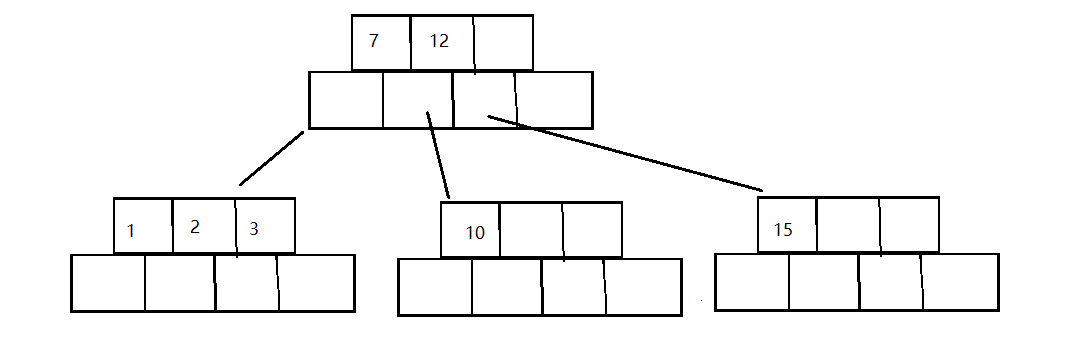
-
发现条件不满足——分裂
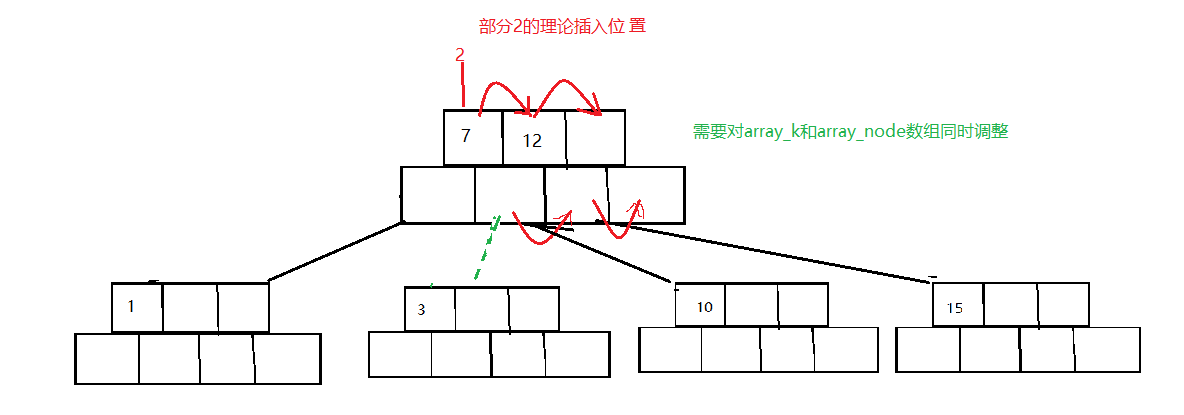
-
调整后
-
此时父节点已经不满足B树的规则继续调整
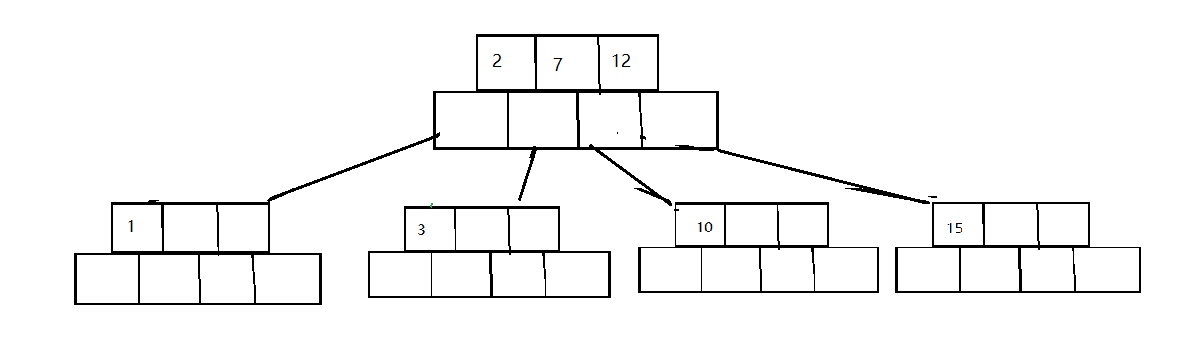
-
在进行分裂
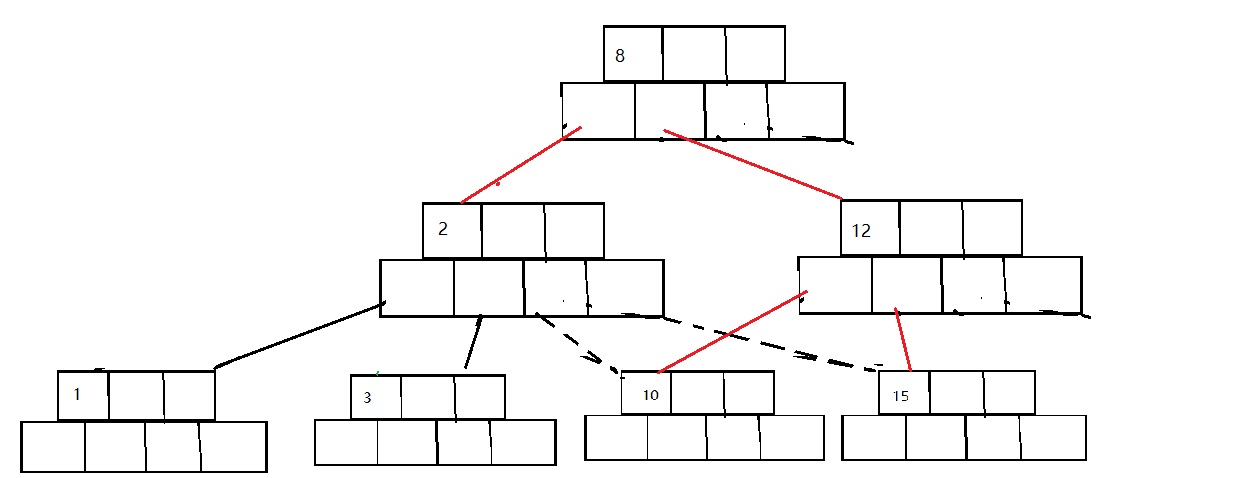
注意
上文在介绍树节点的数据结构的时候不论是array_k还是array_node的时候都比B树规定的多开了一个空间,到这里你应该能体会到为什么了吧?
目的就是为了将插入和分裂两个过程解耦,不然插入和分裂弄在一块就会很麻烦
B树的删除
B树的删除思路如下
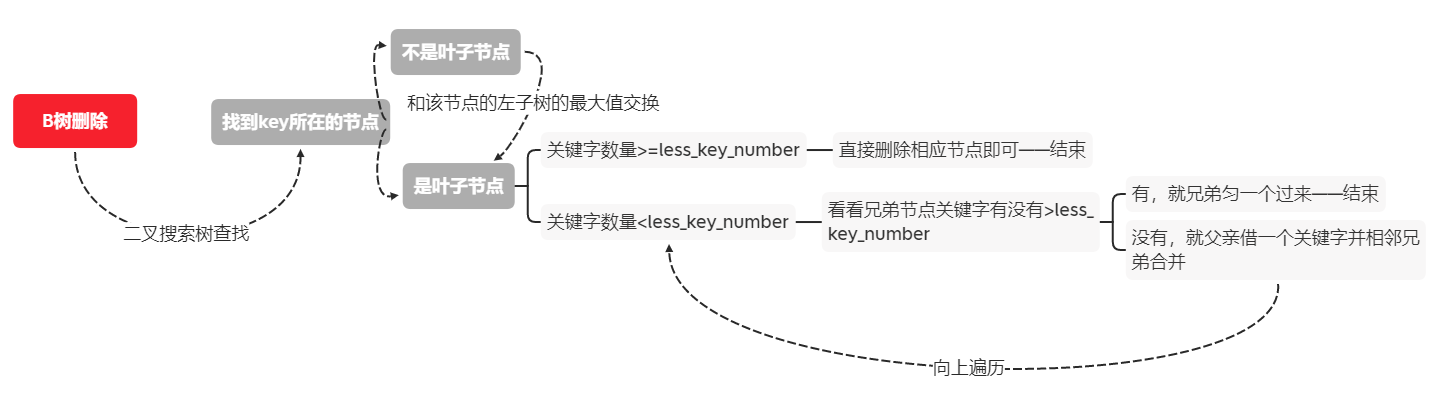
下面我将举几个例子来带大家深入对删除规则的理解:
以下面👇这个B树为例:通过删除不同的关键字来将删除思路中的不同情况加以说明
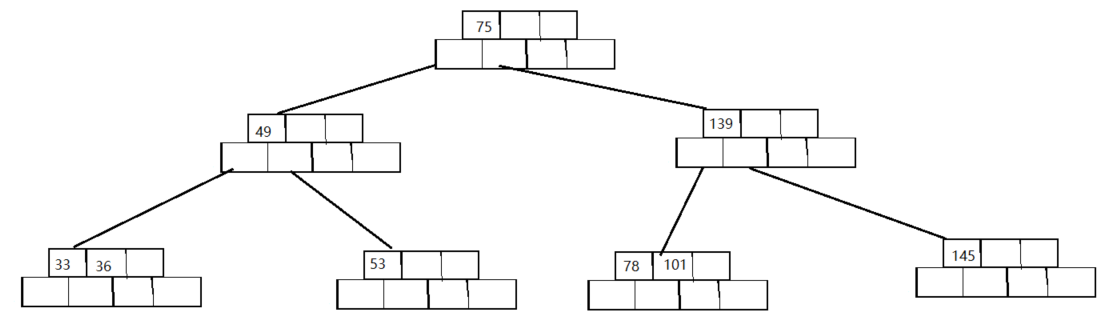
-
情况一
对下面这个B树删除关键字33

- 首先先要删除关键字所在的叶子节点——然后直接删除(注意这里的删除需要调整array_key数组)
- 删除之后,发现该节点的关键字数量依然
>=less_key_number,所以不用调整
最后的删除结果如下
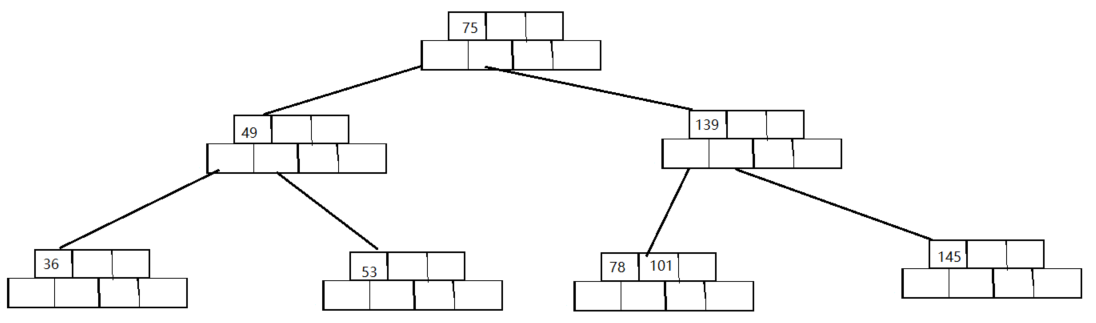
-
情况二
还是删除这个B树👇删除关键字53
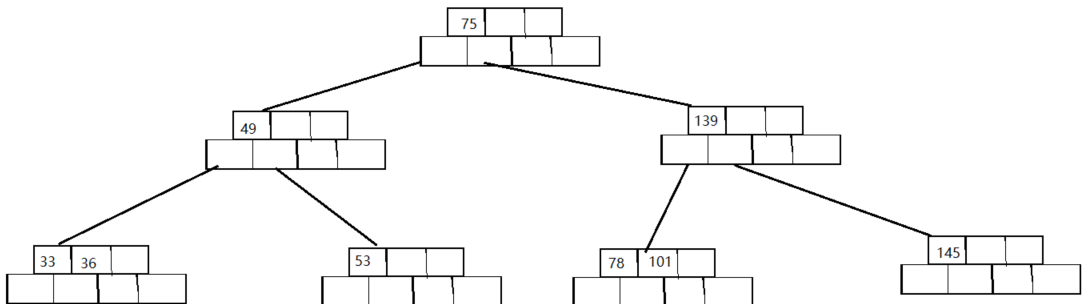
- 所有删除的前面两步都是相同的——找到要删除关键字所在的节点,直接删除该关键字
- 删除53关键字之后,该节点的关键字个数
<less_key_number需要调整 - 这时优先向兄弟节点借关键字(这里还有一个潜台词:兄弟节点的关键字数量一定是
>=less_key_number),看看兄弟节点是否有多余的关键字(多余指的是:关键字数量>less_key_number),然后我们发现很好有一个兄弟节点bro多出了一个关键字
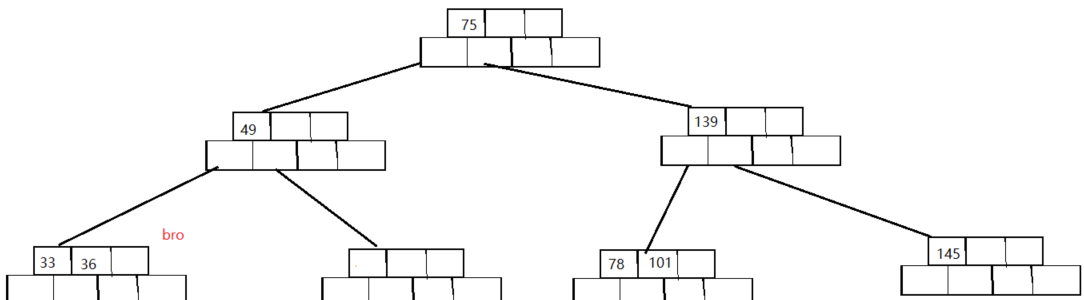
- 最后就是移动节点环节,由于移动的过程中要保持是一个B树,所以bro节点和删除节点中间的子节点都需要移动,同时不仅需要移动
array_node数组还需要移动array_k数组
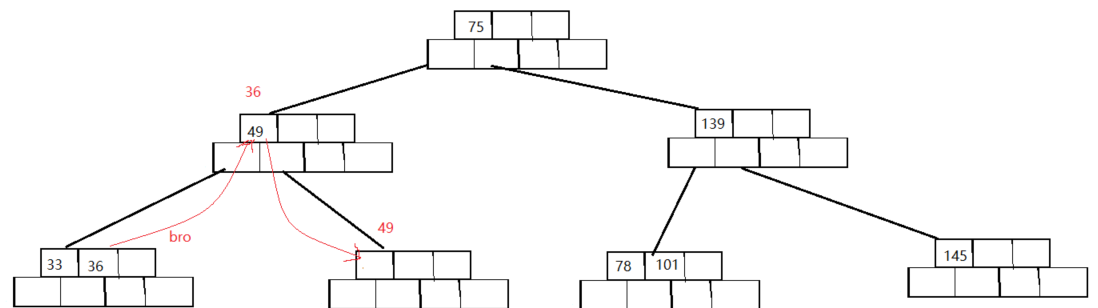
最终结果就是:
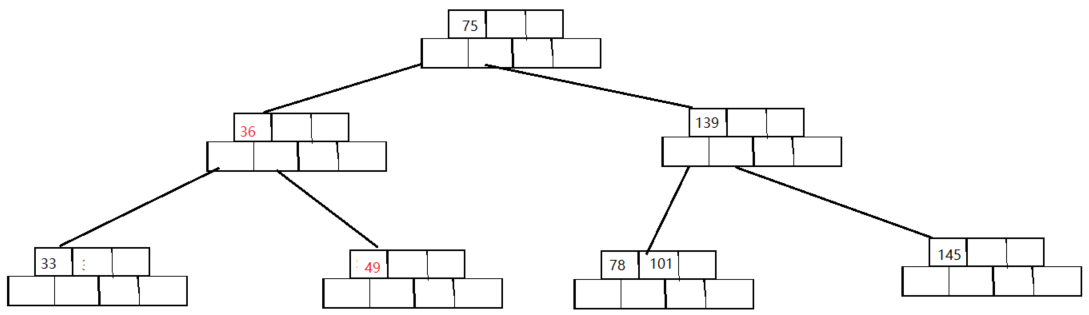
-
情况三
对下面这个B树删除关键字49
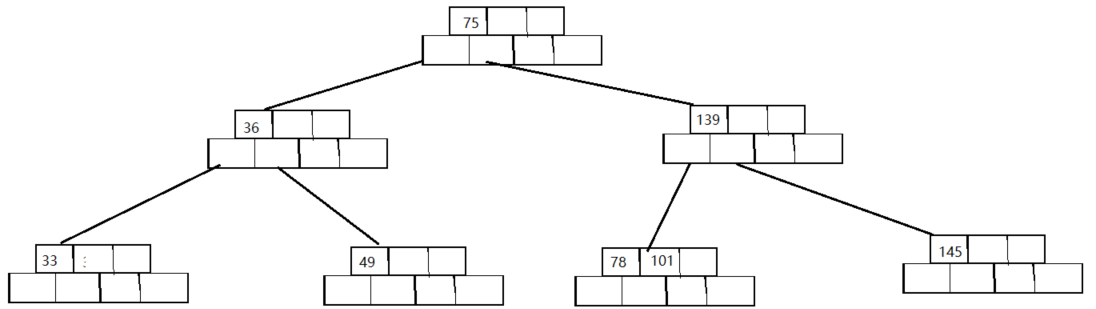
-
和前面一样前两步依然一样:找到关键字所在节点,删除关键字
-
删除完了之后,我们发现不满足关键字数量
>=less_key_number于是我们优先看看兄弟节点是否有多余的关键字 -
找了一圈发现兄弟也没有多余的(注意这里的情况有一个潜台词:所有兄弟节点的关键字数量等于
less_key_number,如果兄弟节点关键字数量大于less_key_number一定可以借给删除节点,如果小于less_key_number则不符合B树的定义),这时只能向爸爸(父节点)借🤣,由于父节点被接走了一个关键字此时还必须满足关键字数量==子节点数量-1,所以删除节点还需要和一个兄弟节点合并。
我们现在来计算一下合并后的新节点的关键字数量:less_key_number-1(删除节点的关键字数量)+ 1(从父节点借的关键字)+less_key_number(兄弟节点的关键字数量:上面论证过为什么一定等于这个数)=2*less_key_number。而上文我们已经知道less_key_number<M/2(不取整),所以2*less_key_number一定小于等于M-1
注意:在合并的过程中array_k数组和array_node数组两个都需要调整,你叶子节点调不调整看不出来,但是中间节点不调整就会出问题
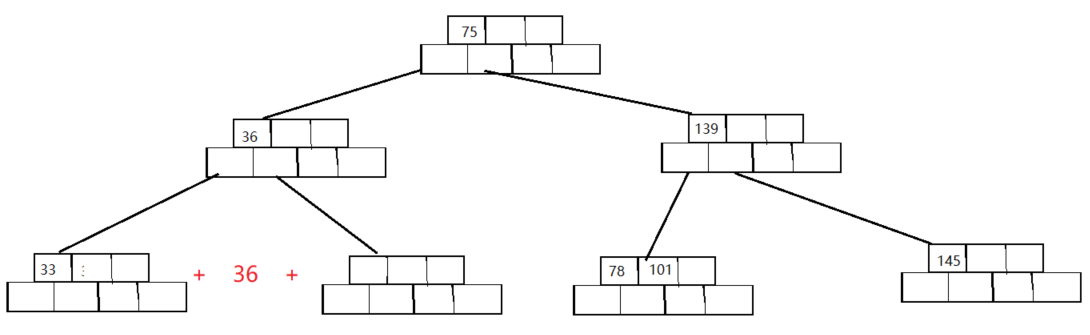
合并之后:
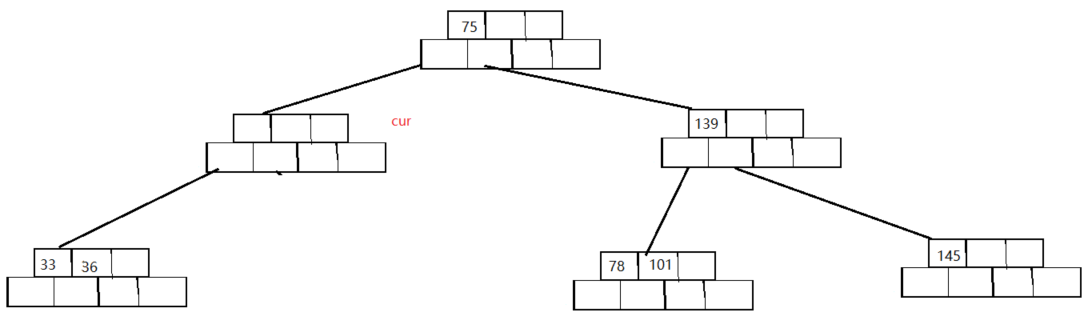
注意虽然这里的cur节点一个关键字没有,他依然满足关键字数量==子节点数量-1 -
这时我们把cur节点当做被删除节点,重复上述步骤
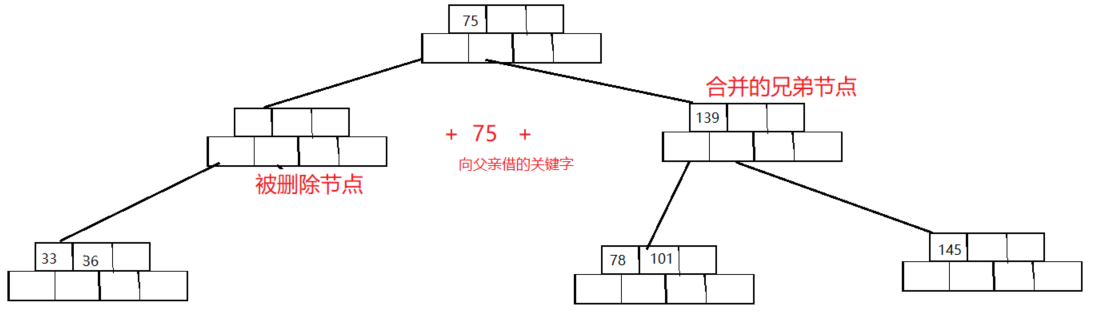
最终得到:
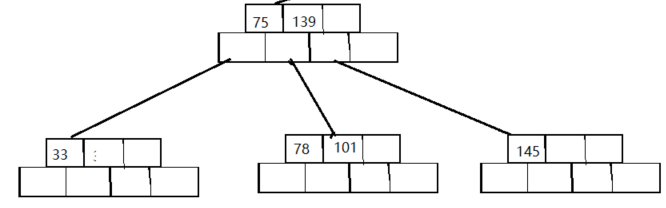
-
-
情况四
-
上面删除的关键字无一例外的都是叶子节节点的关键字,如果删除的关键字不在叶子节点怎么办?这个思路也很简单——找删除关键字所在节点左子树的最大值 或 右子树的最小值 替换,替换完之后又变成了叶子节点删除。这个在红黑树和AVL树中都有体现就不细说了
B树的模拟实现
模拟实现了一下,通过了自己编的一些测试用例,不保证对🤗
代码









![[Data structure]单链表常见算法题](https://img-blog.csdnimg.cn/bdee3d0d769048deba2409a36830c0fc.png)