目录
一、动态规划的基本思想
二、设计动态规划法的步骤
三、动态规划问题的特征
4.1 矩阵连乘积问题
4.1.1 分析最优解的结构
4.1.2 建立递归关系
4.1.3 计算最优值
4.1.3 计算最优值
4.1.3 构造最优解
4.2 动态规划算法的基本要素
4.2.1 最优子结构
4.2.2 重叠子问题
算法4.3 计算矩阵连乘积的递归算法
4.1.3 备忘录方法
算法4.4计算矩阵连乘积的备忘录算法
编辑
4.3 最长公共子序列
4.3.2 子问题的递归结构
4.3.3 计算最优值
4.4 最大子段和
一、动态规划的基本思想
- 动态规划算法通常用于求解具有某种最优性质的问题。
- 在这类问题中,可能会有许多可行解。
- 基本思想是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
- 如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。
- 这就是动态规划法的基本思路。
二、设计动态规划法的步骤
三、动态规划问题的特征
- 动态规划算法的有效性依赖于问题本身所具有的两个重要性质:
- 当问题的最优解包含了其子问题的最优解时,称该问题具有最优子结构性质。
- 在用递归算法自顶向下解问题时,每次产生的子问题并不总是新问题,有些子问题被反复计算多次。动态规划算法正是利用了这种子问题的重叠性质,对每一个子问题只解一次,而后将其解保存在一个表格中,在以后尽可能多地利用这些子问题的解。
4.1 矩阵连乘积问题
- m×n矩阵A与n×p矩阵B相乘需耗费 的时间。
- 我们把mnp作为两个矩阵相乘所需时间的测量值。
- 现在假定要计算三个矩阵A、B和C的乘积,有两种方式计算此乘积。
- 尽管这两种不同的计算顺序所得的结果相同,但时间消耗会有很大的差距。


- 定义:给定n个矩阵{A1,A2,…,An},其中Ai与Ai+1是可乘的,i=1,2,…n-1。考察这n个矩阵的连乘积A1A2…An。
- 由于矩阵乘法满足结合律,所以计算矩阵的连乘可以有许多不同的计算次序。
- 这种计算次序可以用加括号的方式来确定。
- 若一个矩阵连乘积的计算次序完全确定,也就是说该连乘积已完全加括号,则可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积
- 完全加括号的矩阵连乘积可递归地定义为:
- 设有四个矩阵A, B, C, D,总共有五种完全加括号的方式:
(A((BC)D))
(A(B(CD)))
((AB)(CD))
(((AB)C)D)
((A(BC)D))
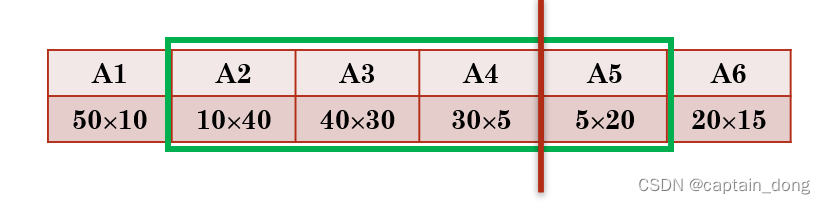
- 设有四个矩阵A, B, C, D,它们的维数分别是:
A=50×10, B=10×40, C=40×30, D=30×5
- 矩阵A和B可乘的条件: 矩阵A的列数等于矩阵B的行数。
- 设A是p×q的矩阵, B是q×r的矩阵, 乘积是p×r的矩阵;
- 上述5种完全加括号方式的计算工作量为:
(A((BC)D)), (A(B(CD))), ((AB)(CD)), (((AB)C)D), ((A(BC)D))
16000, 10500, 36000, 87500, 34500
BC: 10×40×30 = 12000,
(BC)D: 10×30×5 = 1500,
(A((BC)D)): 50×10×5 = 2500
- 给定n个矩阵{A1,A2,…,An},其中Ai与Ai+1是可乘的,i=1,2…,n-1。如何确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的数乘次数最少?
- 穷举法:列举出所有可能的计算次序,并计算出每一种计算次序相应需要的数乘次数,从中找出一种数乘次数最少的计算次序。

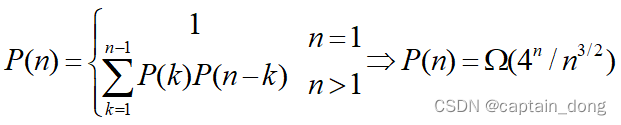
4.1.1 分析最优解的结构
- 将矩阵连乘积AiAi+1…Aj 简记为A[i:j], 这里i≤j;
- 考察计算A[1:n]的最优计算次序。
- 设这个计算次序在矩阵Ak和Ak+1之间将矩阵链断开,1≤k<n,则其相应完全加括号方式为(A1A2…Ak)(Ak+1Ak+2…An)
- 计算量:A[1:k]的计算量加上A[k+1:n]的计算量,
- 再加上A[1:k]和A[k+1:n]相乘的计算量
- 特征:计算A[1:n]的最优次序所包含的计算矩阵子链 A[1:k]和A[k+1:n]的次序也是最优的。
- 矩阵连乘计算次序问题的最优解包含着其子问题的最优解。
- 这种性质称为最优子结构性质。
- 问题的最优子结构性质是该问题可用动态规划算法求解的显著特征。
4.1.2 建立递归关系


4.1.3 计算最优值
- 对于1≤i≤j≤n不同的有序对(i, j)对应于不同的子问题。因此,不同子问题的个数最多只有
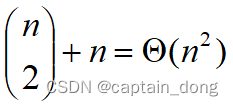
- 在递归计算时,许多子问题被重复计算多次。
- 这也是该问题可用动态规划算法求解的又一显著特征。
- 用动态规划算法解此问题,可依据其递归式以自底向上的方式进行计算。
- 在计算过程中,保存已解决的子问题答案。
- 每个子问题只计算一次,在后面需要时只要简单查一下,从而避免大量的重复计算,最终得到多项式时间的算法。

#define NUM 51
int p[NUM];
int m[NUM][NUM];
int s[NUM][NUM];
void MatrixChain (int n)
{
for (int i=1; i<=n; i++) m[i][i] = 0;
for (int r=2; r<=n; r++)
for (int i=1; i<=n-r+1; i++)
{
int j=i+r-1;
//计算初值,从i处断开
m[i][j] = m[i+1][j]+p[i-1]*p[i]*p[j];
s[i][j] = i;
for (int k=i+1; k<j; k++)
{
int t = m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if (t < m[i][j]) {m[i][j] = t; s[i][j] = k;}
}
}
}
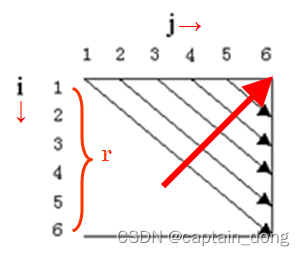
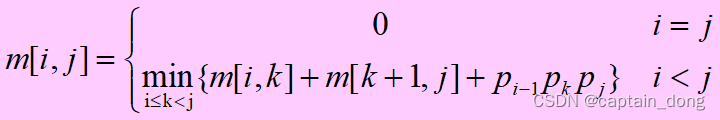
4.1.3 计算最优值
计算顺序
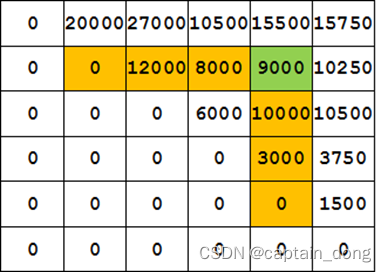

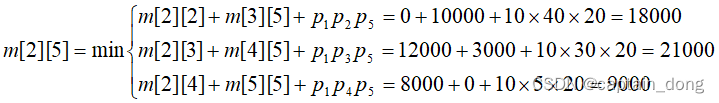
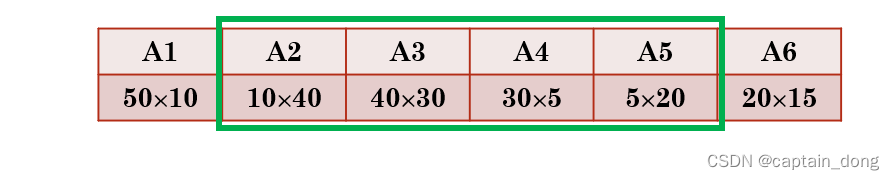
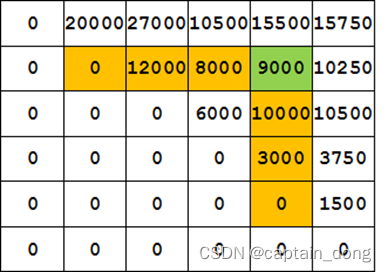
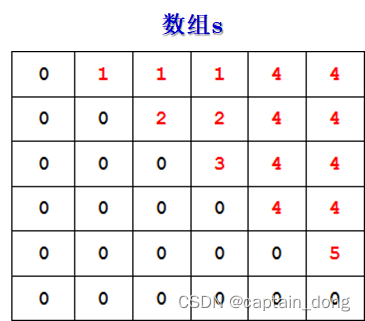
- 依据其递归式以自底向上的方式进行计算。
- 在计算过程中 , 保存已解决的子问题答案。
- 每个子问题只计算一次 , 而在后面需要时只要简单查一下 ,从而避免大量的重复计算, 最终得到多项式时间的算法。


计算顺序
4.1.3 构造最优解
- s[i][j]已经存储了构造最优解所需要的足够的信息。
- 每个部分的最优加括号方式可以根据数组s的相应元素得出。
- 照此递推下去,最终可以确定A[1:n]的最优完全加括号方式,即构造出问题的一个最优解。
//算法4.2计算矩阵连乘积最优解的递归算法
void TraceBack(int i, int j)
{
if(i==j) printf("A%d", i);
else
{
printf("(");
TraceBack(i,s[i][j]);
TraceBack(s[i][j]+1,j);
printf(")");
}
}

4.2 动态规划算法的基本要素
4.2.1 最优子结构
- 设计动态规划算法的第一步是刻画最优解的结构。
- 当问题的最优解包含其子问题的最优解时,称该问题具有最优子结构性质。
- 问题的最优解子结构性质提供了该问题可用动态规划求解的重要线索。
- 动态规划算法中,利用问题的最优子结构性质,以自底向上的方法递归的从子问题的最优解逐步构造出整个问题的最优解。
- 使我们能在相对小的子问题空间中考虑问题。
4.2.2 重叠子问题
- 递归算法求解问题时,每次产生的子问题并不总是新问题,有些子问题被反复计算多次。
- 这种性质称为子问题的重叠性质。
- 动态规划算法,对每一个子问题只解一次,而后将其解保存在一个表格中,当再次需要解此子问题时,只是简单地用常数时间查看一下结果。
- 通常不同的子问题个数随问题的大小呈多项式增长。
- 用动态规划算法只需要多项式时间,从而获得较高的解题效率。

算法4.3 计算矩阵连乘积的递归算法
//算法4.3 计算矩阵连乘积的递归算法
int Recurve(int i, int j)
{
if (i == j) return 0;
int u = Recurve(i, i)+Recurve(i+1,j)+p[i-1]*p[i]*p[j];
s[i][j] = i;
for (int k = i+1; k<j; k++)
{
int t = Recurve(i, k) + Recurve(k+1,j)+p[i-1]*p[k]*p[j];
if (t<u) { u = t; s[i][j] = k;}
}
m[i][j] = u;
return u;
}
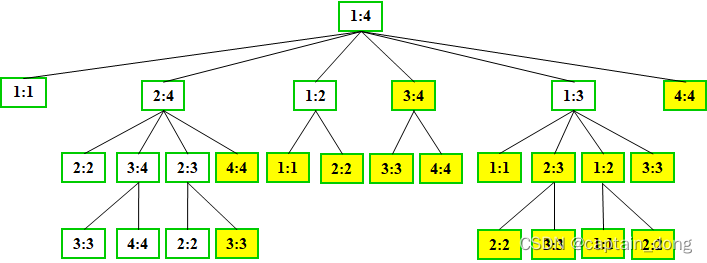
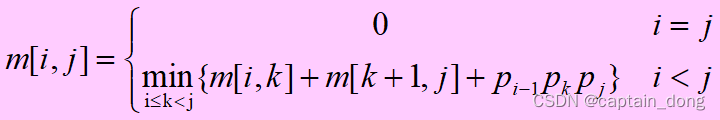
4.1.3 备忘录方法
- 备忘录方法是动态规划算法的变形。
- 与动态规划算法一样,备忘录方法用一个表格保存已解决的子问题的答案,再碰到该子问题时,只要简单地查看该子问题的解答,而不必重新求解。
- 备忘录方法的控制结构与直接递归方法的控制结构相同,区别仅在于备忘录方法为每个解过的子问题建立了备忘录以备需要时查看,避免了相同子问题的重复求解。
算法4.4计算矩阵连乘积的备忘录算法
int LookupChai (int i, int j)
{
if (m[i][j]>0) return m[i][j];
if (i==j) return 0;
int u = LookupChain(i,i)+LookupChain(i+1,j)+p[i-1]*p[i]*p[j];
s[i][j] = i;
for (int k = i+1; k<j; k++)
{
int t = LookupChain(i,k)+LookupChain(k+1,j)+p[i-1]*p[k]*p[j];
if (t < u) { u = t; s[i][j] = k;}
}
m[i][j] = u;
return u;
}
4.3 最长公共子序列
- 若给定序列X={x1,x2,…,xm},则另一序列Z={z1,z2,…,zk},是X的子序列是指存在一个严格递增下标序列{i1,i2,…,ik}使得对于所有j=1,2,…,k有:zj=xij。
- 例如,序列Z={B,C,D,B}是序列X={A,B,C,B,D,A,B}的子序列,相应的递增下标序列为{2,3,5,7}。
- 给定2个序列X和Y,当另一序列Z既是X的子序列又是Y的子序列时,称Z是序列X和Y的公共子序列。
- 给定2个序列X={x1,x2,…,xm}和Y={y1,y2,…,yn},找出X和Y的最长公共子序列。
- 设序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}的最长公共子序列为Z={z1,z2,…,zk} ,则
- 若xm=yn,则zk=xm=yn,且zk-1是xm-1和yn-1的最长公共子序列。
- 若xm≠yn且zk≠xm,则Z是xm-1和Y的最长公共子序列。
- 若xm≠yn且zk≠yn,则Z是X和yn-1的最长公共子序列。

4.3.2 子问题的递归结构
- 由最长公共子序列问题的最优子结构性质可知,要找出X和Y的最长公共子序列,可按以下方式递归地进行:
- 当xm=yn时,找出Xm-1和Yn-1的最长公共子序列,然后在其尾部加上xm(=yn)即可得X和Y的一个最长公共子序列。
- 当xm≠yn时,必须解两个子问题,即找出Xm-1和Y的一个最长公共子序列及X和Yn-1的一个最长公共子序列。这两个公共子序列中较长者为X和Y的一个最长公共子序列。
- 用c[i][j]记录序列和的最长公共子序列的长度。
- Xi={x1,x2,…,xi};Yj={y1,y2,…,yj}。
- 当i=0或j=0时,空序列是Xi和Yj的最长公共子序列。
- 故此时C[i][j]=0。
- 其它情况下,由最优子结构性质可建立递归关系如下:
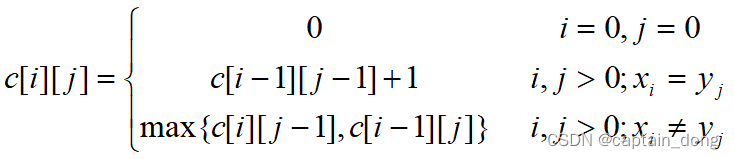
4.3.3 计算最优值
//算法4.5计算最长公共子序列的动态规划算法
#define NUM 100
int c[NUM][NUM];
int b[NUM][NUM];
void LCSLength (int m, int n, const char x[],char y[])
{
int i,j;
//数组c的第0行、第0列置0
for (i = 1; i <= m; i++) c[i][0] = 0;
for (i = 1; i <= n; i++) c[0][i] = 0;
//根据递推公式构造数组c
for (i = 1; i <= m; i++)
for (j = 1; j <= n; j++)
{
if (x[i]==y[j])
{c[i][j]=c[i-1][j-1]+1; b[i][j]=1; } //↖
else if (c[i-1][j]>=c[i][j-1])
{c[i][j]=c[i-1][j]; b[i][j]=2; } //↑
else { c[i][j]=c[i][j-1]; b[i][j]=3; } //←
}
}

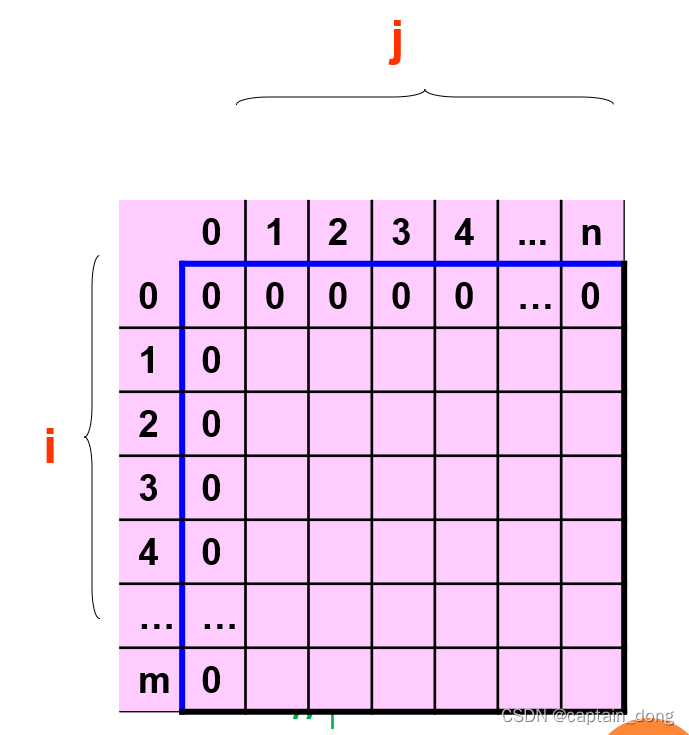



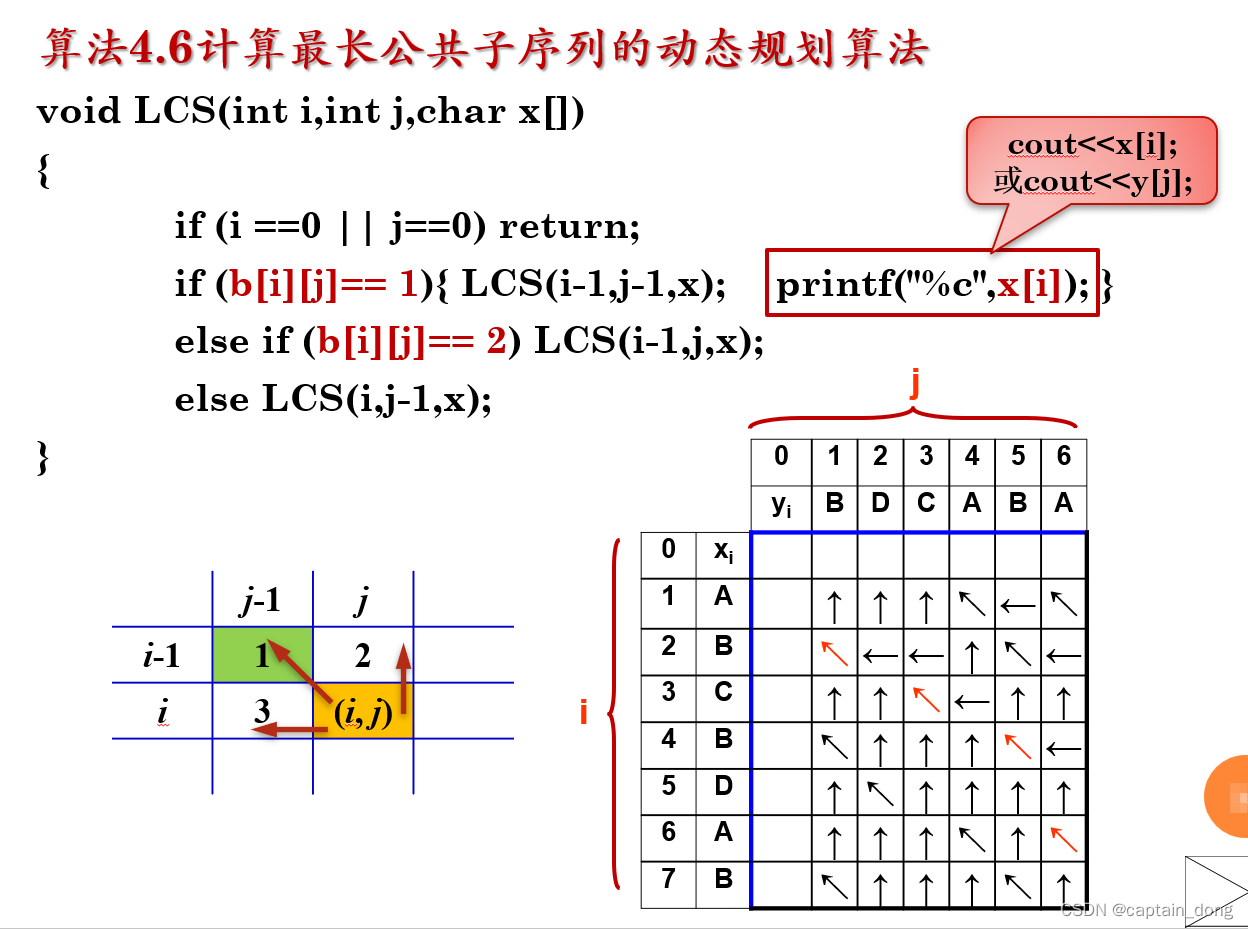
4.4 最大子段和
- 给定由n个整数(包含负整数)组成的序列a1,a2,...,an,求该序列子段和的最大值。
- 当所有整数均为负值时定义其最大子段和为0。
- 所求的最优值为:
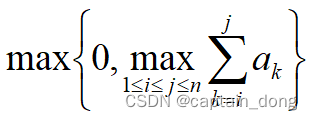
- 例如,当(a1,a2, ……a7,a8)=(1,-3, 7,8,-4,12, -10,6)时,最大子段和为:
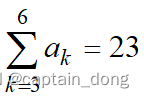
- bj是1到j位置的最大子段和:
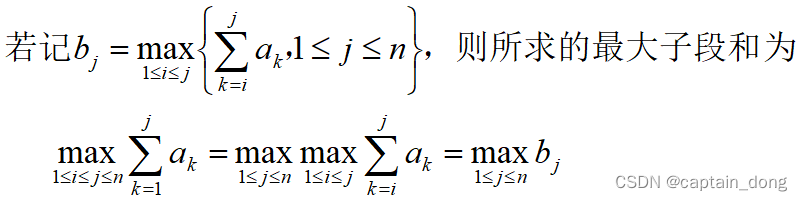







![[计算机图形学]动画与模拟:关键帧动画、质点弹簧系统、运动学与绑定(前瞻预习/复习回顾)](https://img-blog.csdnimg.cn/79ea2d973dfc47b59d0f43d376d1fe65.png)




