学习目标:
掌握n阶行列式的定义和计算方法,并能够解决相关的数学问题。
学习步骤:
学习n阶行列式的定义,需要一定的抽象思维能力和数学基础。
-
了解基本概念和性质:在学习n阶行列式之前,需要先了解行列式的基本概念和性质。这包括行列式的定义、展开式、性质和应用等方面。可以通过教材、课程讲义和在线资源等途径来学习。
-
掌握计算方法:n阶行列式的计算方法比较繁琐,需要掌握具体的计算方法和技巧。例如,可以使用余子式和代数余子式的方法进行计算,或者使用行变换和列变换等方法简化计算。
-
做练习和例题:在学习n阶行列式的定义过程中,需要进行大量的练习和例题,以加深理解和掌握计算方法。可以使用教材或者在线资源上的练习题和例题来进行练习。
-
参考其他学习资源:除了教材和课程讲义之外,还可以参考其他学习资源,如数学论文、研究报告、网上教程和视频讲座等,以便更全面地了解n阶行列式的定义和应用。
总之,学习n阶行列式的定义需要进行系统性的学习和练习,并掌握具体的计算方法和技巧。在学习过程中,可以利用多种资源来帮助自己更好地理解和掌握这一概念。

1.1.1 2阶和3阶行列式的定义
当矩阵为2阶时,它的行列式的定义如下:
$\begin{vmatrix} a_{11} & a_{12}\ a_{21} & a_{22} \end{vmatrix} = a_{11}a_{22} - a_{12}a_{21}$
其中,$a_{11}$、$a_{12}$、$a_{21}$和$a_{22}$分别是2阶矩阵的四个元素。这个行列式可以看成是矩阵的对角线元素之积减去反对角线元素之积。
当矩阵为3阶时,它的行列式的定义如下:
$\begin{vmatrix} a_{11} & a_{12} & a_{13}\ a_{21} & a_{22} & a_{23}\ a_{31} & a_{32} & a_{33} \end{vmatrix} = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} - a_{13}a_{22}a_{31} - a_{11}a_{23}a_{32} - a_{12}a_{21}a_{33}$
其中,$a_{11}$、$a_{12}$、$a_{13}$、$a_{21}$、$a_{22}$、$a_{23}$、$a_{31}$、$a_{32}$和$a_{33}$是3阶矩阵的九个元素。这个行列式可以看成是所有主对角线上元素的积加上所有由三个元素构成的符号相间的三元组的积之和,减去所有副对角线上元素的积加上所有由三个元素构成的符号相间的三元组的积之和。
这些定义给出了2阶和3阶行列式的具体计算公式。在实际计算中,可以使用余子式和代数余子式的方法,或者使用行变换和列变换等方法简化计算。

1.1.2 n阶行列式的定义
当我们要求解一个n阶方阵的行列式时,我们可以使用下面的定义:

其中,$S_n$表示由$n$个元素组成的置换群,$\sigma$是其中一个置换,$sgn(\sigma)$是该置换的符号,$a_{i\sigma(i)}$表示矩阵A中第$i$行第$\sigma(i)$列的元素。
这个定义实际上是在将矩阵的所有行按照某个排列顺序取一个元素,并将这些元素乘起来后累加,其中的符号$sgn(\sigma)$是一个表示该排列的“奇偶性”的符号。
举例来说,对于一个3阶方阵,我们需要考虑所有可能的6种排列方式,并计算每种排列的值,最后将这些值相加,即得到该矩阵的行列式。下面是一个3阶矩阵的例子:

我们按照顺序依次取出第一行的元素$a_{11},a_{12},a_{13}$,第二行的元素$a_{21},a_{22},a_{23}$,第三行的元素$a_{31},a_{32},a_{33}$,并且将它们乘起来。然后,我们考虑所有可能的6种排列方式,并将这些乘积相加。例如,对于排列$\sigma = (1,2,3)$,我们有:

对于排列$\sigma = (1,3,2)$,我们有:

以此类推,最终我们可以得到该矩阵的行列式为:
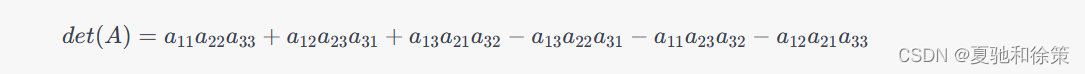
对于任意n阶矩阵,我们也可以按照类似的方法来计算其行列式,只需要依次取出每一行的元素,并考虑所有可能的排列方式即可。




总结:
下面是关于n阶行列式的重点、难点和易错点的总结:
重点:
- n阶行列式是一个关于矩阵的函数,用来描述矩阵的性质和特征。
- 行列式的值可以为正、负或零,代表了矩阵的线性无关性、面积或体积等。
- 行列式的计算可以使用定义式,也可以使用行列式的性质,如行列式的线性性、交换行、相邻行成比例等。
难点:
- 行列式的定义式是一个关于全排列的求和式,需要理解排列的符号和乘积的含义。
- 行列式的计算需要严格按照定义式或行列式的性质进行,需要注意各个元素的位置和符号。
易错点:
- 在使用行列式的性质时,容易出现错误的展开或化简式,需要仔细检查每一步的计算。
- 在计算行列式的值时,容易出现各种算术错误,如乘法错误、加减法错误、符号错误等,需要仔细检查每一步的计算。
总之,对于n阶行列式的学习和掌握,需要对定义式和行列式的性质有深入的理解,同时需要严格按照规定的步骤进行计算,并仔细检查每一步的计算结果,避免出现错误。
宋浩课的笔记:
线性代数和以往的不同
 不同1:矩阵不满足乘法交换律
不同1:矩阵不满足乘法交换律
即AB!=BA
不同2:三个不同的0
0在线性代数有三种可能:
第一个可能 0 是数值0
第二个可能 0 是0矩阵
第三个可能 0 是0向量
为什么有行列式?

1.定义的新运算
行列式其实就是一种数学家们定义出来的新运算(启发:其实新运算在高中时考试或者某些年份的高考早有体现,这都是告诉我们其实很多数学运算都是人们定义出来的,可以说没有人的定义就没有数学)
主次对角线的概念

三阶行列式的求法
这里告诉我具体求解三阶级行列式的求法
排列的概念

注意中间的省略号中不能少,如果是n就一定要用n个数
3145 告诉我他不是排列因为少了2
排列和逆序的概念(这里我的书上没有这个概念):

几种排列的逆序数:
对换和排列定理:
n阶级行列式
行下标的概念
列下标的概念符号由
列坐标奇偶决定了正负性决定的
第一个定义(按行展开):

两种-1绝对值和行列式

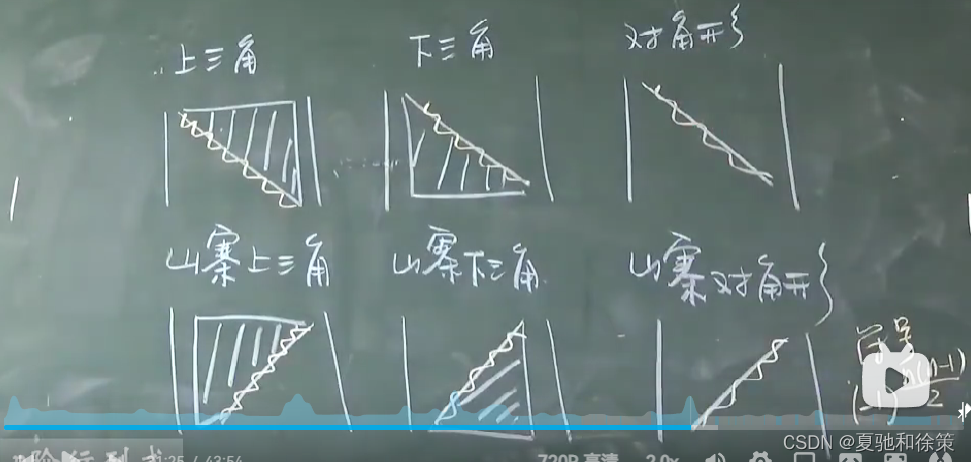
六种形状的行列式