作者：@小萌新
专栏：@算法
作者简介：大二学生希望能和大家一起进步
本篇博客简介：介绍算法的复杂度对数器和二分法

复杂度对数器二分法

复杂度
- 常数时间操作
- 非常数时间操作
- 时间复杂度
- 空间复杂度
二分法
- 有序数组中找一个值
- 寻找有序数组中大于等于某个数的位置
- 无序数组中寻找一个局部最小值

复杂度

常数时间操作

我们把固定时间的操作称为常数时间操作

比如说我们定义两个变量a b

int a;
int b;

在这两个变量进行加减乘除操作的时候它们进行的是固定时间的操作我们就将它们称为常数时间操作

因为在计算机眼里a和b都是由32位的01组成的（在32位的机器上）

不管a和b是什么数字相加在计算机眼里都是进行32位数字的相加所以我们说这个操作是常数时间的

常见的常数时间操作有

常见的算术运算
常见的位运算
赋值比较自增自减操作等
数组寻址

非常数时间操作

我们使用单链表进行查找的时候就是一个非常数时间操作

单链表在内存中的逻辑结构大概是这样子的

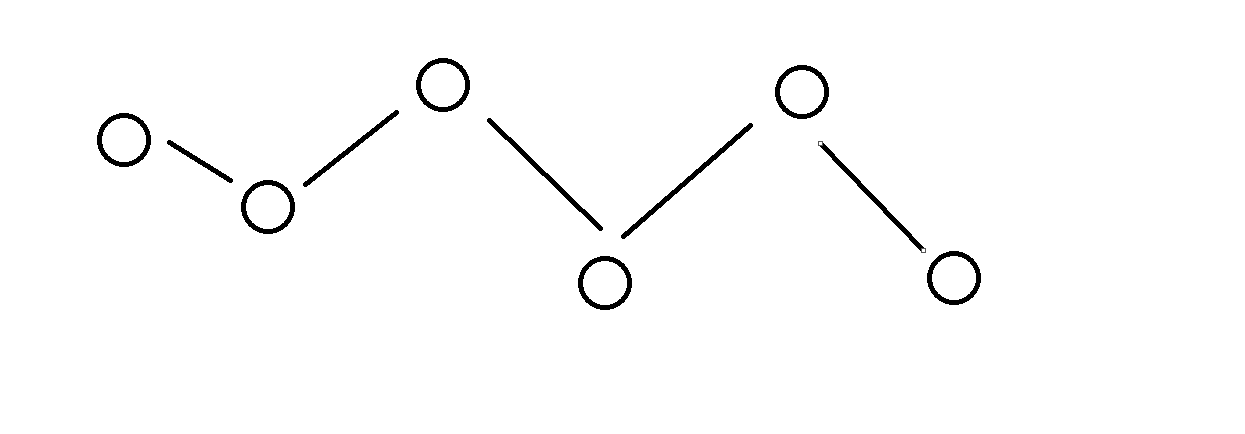
在这里插入图片描述

每个单独的数据通过指针连接起来

我们假设这个单链表中有一千万个数据那么我们查找第20万个数据和第800万个数据的时间肯定是相差很大的这就叫做非常数时间操作

时间复杂度

我们常说的时间复杂度都是使用大O的渐进表示法来表示的

我们使用选择排序的例子来讲解时间复杂度的概念如果对于选择排序有疑问的同学可以参考我的这篇博客

选择排序

简单介绍下选择排序

给我们一个N个无序数字组成的数组

我们首先遍历0~N-1位置找出一个最小的数字和0位置的数字交换位置

之后我们再次遍历1~N-1位置找出一个最小的数字和1位置的数字交换位置

以此类推我们就能得到一个有序的数组

我们上面的算法就叫做选择排序

我们来分析下上面操作的时间复杂度

第一次遍历了N个元素找出最小数字比较了N-1次和0位置交换了一次

第二次遍历了N-1个元素找出最小数字比较了N-2次和0位置交换了一次

以此类推

我们实际的操作次数为 2(N + N-1 + N-2 + N-3 + … + 1) 不难发现前面是一个等差数列

我们根据等差数列公式可以写成以下格式

$aN^2 + bN + c$

其中a b c都是常数我们舍弃掉这些常数再只保留最高阶项

我们就能得到该算法使用大O的渐进表示法的时间复杂度为N的平方

使用大O的渐进表示法的意义

最高阶项对于一个算法的影响是最大的举个实际的例子

假设A算法的时间复杂度为N的三次方系数为1

B算法的时间复杂度为N的平方系数为10

当N为100时候 A算法大概要执行一百万次操作而B算法只需要执行十万次操作就可以了

这还是在N的数字很小的情况下在我们实际的业务逻辑中数字N可能是用万来做单位的

空间复杂度

在除了用户提供给我们的变量空间之外额外开辟的空间叫做空间复杂度我们一般也是使用大O的渐进表示法来表示

用户的输入空间以及用户要求的输出空间都不算是我们额外开辟的空间

比如说上面的选择排序其C++完整代码如下

void selectionsort(int* arr, int size)
{
	// assert
	assert(arr);

	// 还是一样 i控制多少次 j控制每一次的选择排序
	int i = 0;
	int j = 0;
	int maxi = 0;
	int tmp = 0;

	for ( i = 0; i < size-1; i++)
	{
		for (j = 0; j < size - 1 - i; j++)
		{
			if (arr[j]>arr[maxi])
			{
				maxi = j;
			}
		}

		tmp = arr[size - 1 - i];
		arr[size - 1 - i] = arr[maxi];
		arr[maxi] = tmp;
	}
}

除了用户提供给我们的数组之外我们还额外开辟了四个变量这是常数个变量所以说这个算法的空间复杂度是O(1)

给定一个数组要求统计数组里面每个数字出现的次数

我们看这个题目第一时间想到的肯定是使用map来创建一个数字-次数的映射

它的最差情况就是数组中的每个数字都不一样此时我们要开辟的map映射的数量就是n个

所以说该题目的这种解法的空间复杂度都是O(N)

如何比较两个算法的优劣

一般来说我们比较两个算法的优劣都是先比较时间复杂度

假设有AB两个算法 A算法的时间复杂度是N的平方 B算法的时间复杂度是N

此时我们就可以说B算法比A算法更加优秀

但是如果说A B算法的时间复杂度都是N 此时我们就要开始比较空间复杂度比较方式同上

在空间复杂度都相同的情况下我们就不比较常数项了

因为在单次的运算中每种运算所需要的时间就是不同的

比如说位运算就是跑的比加运算要快加运算就是跑的比除运算要快

所以说我们到这个阶段一般会使用大样本的数据直接来测时间

面试竞赛中的算法最优解是什么意思？

一般来说我们在设计一个算法最优解的时候首先要考虑的就是这个算法的时间复杂度

在时间复杂度最低的基础上尽可能的去降低它的空间复杂度

需要注意的是我们比较算法时一般不比较常数项的大小具体原因可以参考上面的内容

如果说两个算法的时空复杂度都一样我们可以认为这两个算法一样优秀

常见的时空复杂度及排名

O(1) > O(logN) > O(N) > O(N*logN) > O(N^2)

二分法

有序数组中找一个值

我们直接来看题目

要求在一个有序的数组中找一个数的下标要你在这个数组中找到该值并且返回它的下标如果找不到就返回-1

如果说我们使用遍历的方式遍历一整个数组的话那么此时我们的时间复杂度就是O(N)了

但是这样子就浪费了有序这一个条件这个时候就可以考虑使用我们的二分法

我们假设该有序数组如下我们要找的元素是4

在这里插入图片描述

我们找到该数组最左边的下标和最右边的下标将它们相加之后除以2 在该题目中我们找到的下标就是4

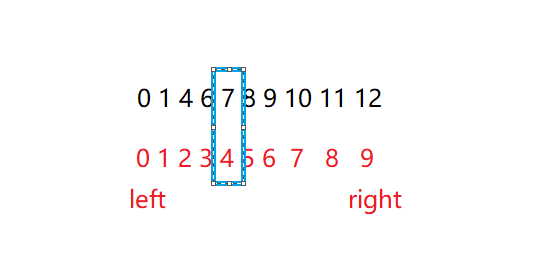
在这里插入图片描述

之后我们比较五下标对应的元素和我们要找的值之间对应的关系之后二分法的精髓就来了

因为该数组为有序数组所以说：

如果中间下标的值大于我们要找的值是不是从中间位置开始整个数组的左半边我们都可以舍弃了
如果中间下标的值小于我们要找的值是不是从中间位置开始整个数组的右半边我们都可以舍弃了

也就是说我们通过一次操作就排除了一半的选项这就是二分法的精髓也是二分法时间复杂度O(logN)的原因

我们下面可以看看代码如何表示

#include <vector>    
#include <iostream>    
using namespace std;    
    
    
int binsearch(vector<int> v , int num)    
{    
  int left = 0;    
  int right = v.size() - 1;    
    
  while(left <= right)    
  {    
    int mid = (left + right) / 2 ;    
    if (v[mid] == num)    
    {    
      return mid;    
    }    
    else if (v[mid] > num)    
    {    
      right = mid - 1;    
    }                                                                                                                                                                             
    else    
    {    
      left = mid + 1;    
    }    
  }    
    
  return -1;    
}    
    
int main()    
{    
  vector<int> v1 = {0 , 1 , 4, 6, 7, 8, 9, 10 , 11 ,12};    
  int ret = binsearch(v1 , 4);    
  cout << ret << endl;    
  return 0;    
}

代码很简单但是这里也有一点小细节需要注意

我们的 left + right 在数组很大的情况下有可能会产生溢出的情况

所以说我们可以采用这种写法

		// mid = (left + right) /2  防止溢出 
		mid = left + (right - left) / 2;

该代码运行结果如下

在这里插入图片描述

下标确实是2 符合我们的预期

寻找有序数组中大于等于某个数的位置

给你一个有序数组要求你找到从某个值开始后面的所有值都大于等于我们的key值

该题目也是一个典型的二分法的应用

我们假设有序数组如下要求我们从某个下标开始所有值都大于等于三
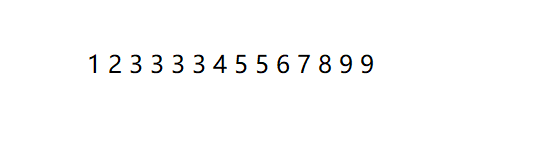
在这里插入图片描述

还是和上面的思路一样我们找出该数组的左右下标之后找出中间位置

在这里插入图片描述

如果该下标对应的值大于等于我们key值那么我们就记录下该下标之后排除掉右边所有的值
如果该下标对应的值小于我们的key值那么我们就排除掉左边所有的值

和第一个题目不同的是我们在做该题时一次二分并不能找到我们的答案必须要二分到最后一个值才能确定我们的答案是多少（因为可能会有重复的值）

这也是我们记录下标的意义每次找到符合要求的下标我们就更新它

代码如下

#include <iostream>    
using namespace std;    
#include <vector>    
    
void binsearch(vector<int> v , int num)    
{    
  int left = 0;    
  int right = v.size() -1 ;    
  int index = 0;    
  while(left <= right)    
  {    
    int mid = left + ((right - left) / 2);    
    if (v[mid] >= num)    
    {    
      index = mid;    
      right = mid -1;    
    }    
    else    
    {    
      left = mid + 1;    
    }    
  }    
    
  cout << "find the index is:" << index << endl;    
}    
    
    
int main()    
{    
  vector<int> v1 = {1 , 2 , 3, 3, 3, 4, 5, 5, 6, 7, 8, 9, 9, 9};    
  binsearch(v1 , 3);                                                                                                                                                              
  return 0;    
}

运行结果如下

在这里插入图片描述

我们发现确实符合我们的预期

总结：

从这个题目中我们应该能够加深对于二分法的理解它的特点在于能够一次性排除一半的值

通过这个特点我们能够很快速的在有序数组中找到某一个特定的位置

无序数组中寻找一个局部最小值

给你一个无序数组（数组元素大于3）该数组中每个元素都不相等要求你找到一个局部最小值

我们这里首先给出一个局部最小值的概念

如果这个值比它前一个位置和后一个位置的值都小那么我们就认为这个值是一个局部最小值

如果是起始位置和终止位置我们就只需要比较它和后一个（前一个）位置就可以

明白局部最小值的概念之后我们肯定会先考虑两个特殊位置最前面和最后面的位置

如果说这其中有一个位置是局部最小值我们直接返回就好了

如果说它们都不是一个局部最小值那么该数组的大小排序应该是一个这样子的状态

在这里插入图片描述

中间是一个什么状态我们不知道但是根据起始和终止位置我们能够推断的是中间肯定会存在一个局部最小值

因为只有存在一个局部最小值该曲线到最后才会是一个上升的状态否则就会是一直下降了

那么我们就可以通过二分法来找到这其中一个局部最小值

我们通过二分法找到中间位置之后该位置和相邻两个位置的关系只可能是这三种

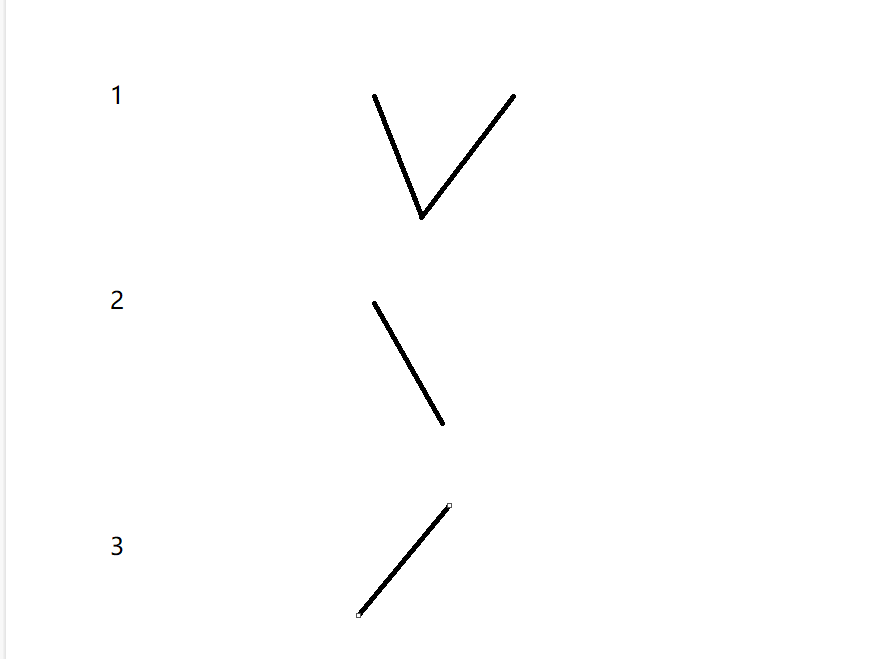
在这里插入图片描述

如果是第一种情况那么我们就可以直接返回该下标的位置因为这就是一个局部最小值

如果是情况二我们可以画出这样子的图来理解

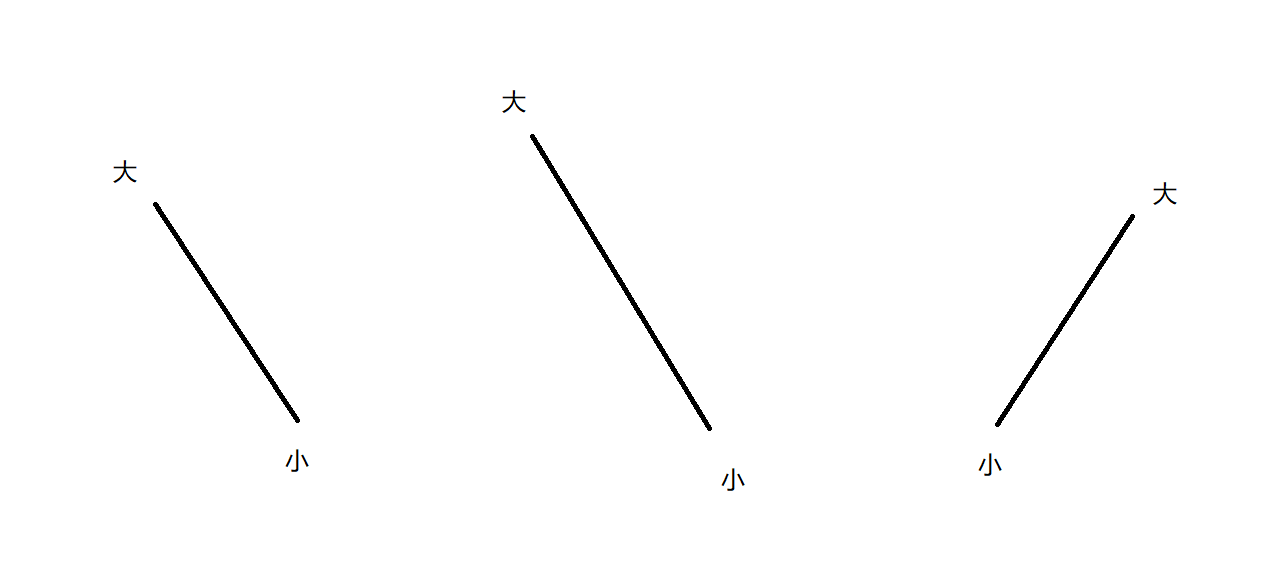
在这里插入图片描述

通过这张图我们就可以推断出右边肯定会存在一个局部最小值可以继续二分

同理如果是情况三

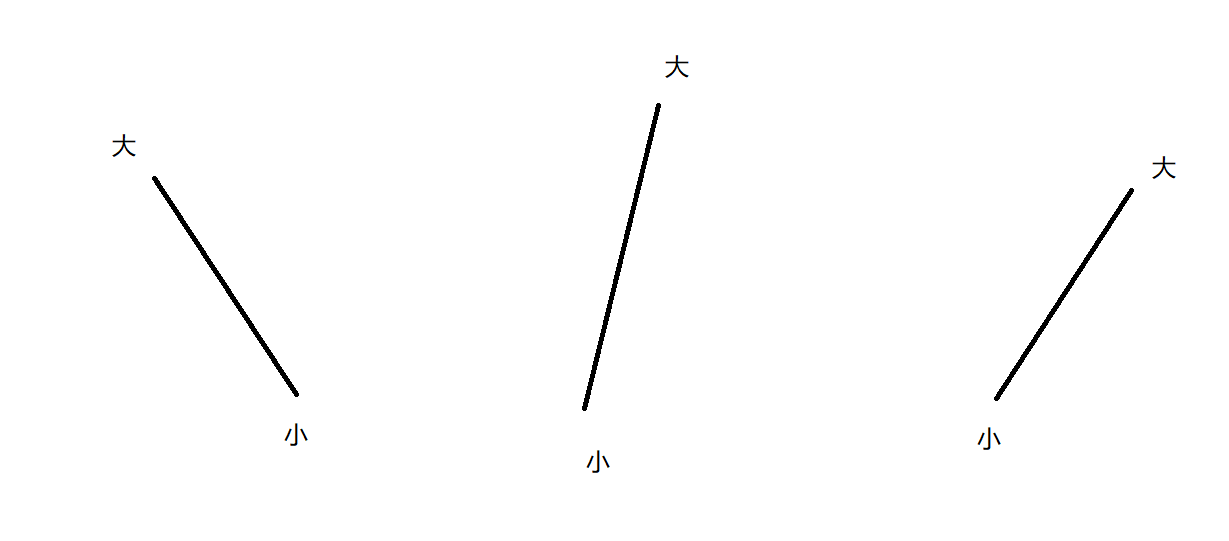
在这里插入图片描述
我们可以推断出左边肯定会存在一个局部最小值可以继续二分

#include <iostream>
using namespace std;
#include <vector>

void binsearch(vector<int>& v1)
{
  int left = 0;
  int right = v1.size() -1;
  // left 
  if (v1[1] > v1[0])
  {
    cout << "find the min num:" << v1[left] << "index:" << left << endl;
    return;
  }
  // right 
  if (v1[right -1 ] > v1[right])
  {
    cout << "find the min num:" << v1[right] << "index:" << right << endl;
    return;    
  }    
    
  while(left <= right)    
  {
    int mid = (left + right) / 2;                                                                                                                                                                     
    if (v1[mid] < v1[mid - 1])    
    {    
      if (v1[mid] < v1[mid + 1])    
      {    
        cout << "find the min num:" << v1[mid] << "  index:  " << mid << endl;    
        return;    
      }    
      else    
      {    
        left = mid + 1;    
      }    
    }    
    else    
    {    
      right = mid - 1;    
    }    
  }    
} 

int main()
{
  vector<int> v1 = {3 , 1, 5, 6, 7, 5, 7, 8, 1, 9};
  binsearch(v1);
  return 0;
}