目录

舵机的工作原理

案例程序

要求：

程序：

---

二维云台是通过IIC总线进行控制的，我们可以通过窗口命令输入：i2cdetect -y 1来检测IIC总线是否连接正常。

当有40显示的时候就说明IIC总线正常。

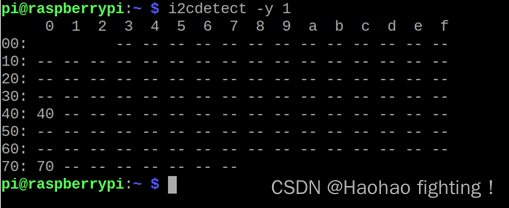
 操控舵机我们需要一个PCA9685的模块，用到“Adafruit_PCA9685”的库函数，需要我们在官网下载。具体步骤：

树莓派下安装PCA9685的python驱动程序_树莓派安装adafruit_pca9685库_Ryan.Mo的博客-CSDN博客

舵机的工作原理

舵机的伺服系统由可变宽度的脉冲来进行控制，控制线是用来传送脉冲的。脉冲的参数有最小值，最大值，和频率。

一般而言，舵机的基准信号都是周期为20ms，宽度为1.5ms。

这个基准信号定义的位置为中间位置。舵机有最大转动角度，中间位置的定义就是从这个位置到最大角度与最小角度的量完全一样。最重要的一点是，不同舵机的最大转动角度可能不相同，但是其中间位置的脉冲宽度是一定的，那就是1.5ms。

 

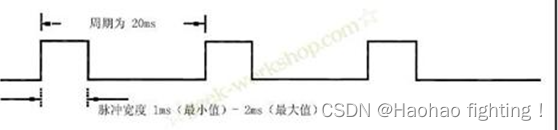
 角度是由来自控制线的持续的脉冲所产生。这种控制方法叫做脉冲调制。脉冲的长短决定舵机转动多大角度。

例如：1.5毫秒脉冲会到转动到中间位置（对于180°舵机来说，就是90°位置）。当控制系统发出指令，让舵机移动到某一位置，并让他保持这个角度，这时外力的影响不会让他角度产生变化，但是这个是由上限的，上限就是他的最大扭力。除非控制系统不停的发出脉冲稳定舵机的角度，舵机的角度不会一直不变。

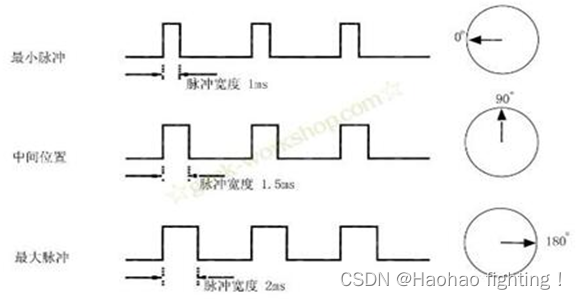
当舵机接收到一个小于1.5ms的脉冲，输出轴会以中间位置为标准，逆时针旋转一定角度。接收到的脉冲大于1.5ms情况相反。不同品牌，甚至同一品牌的不同舵机，都会有不同的最大值和最小值。

一般而言，最小脉冲为1ms，最大脉冲为2ms。

 

案例程序

要求：

该程序中，舵机的工作频率是50HZ（周期20ms），脉冲宽度：1-2ms，

向其数据端子施加1ms的高脉冲时，舵机的角度为0°；

向其数据端子施加1.5ms的高脉冲时，舵机的角度为90°；

向其数据端子施加2ms的高脉冲时，舵机的角度为180°。

程序：

pwm = Adafruit_PCA9685.PCA9685() #创建一个 PWM 实例

配置最小和最大伺服脉冲宽度

servo_min = 150  # Min pulse length out of 4096

servo_max = 600  # Max pulse length out of 4096

下面就是新定义两个函数 ：set_servo_pulse和set_servo_angle ，使设置伺服脉冲宽度更简单。

第一个函数：该函数两个参数，第一个是通道，也就是具体是哪一个舵机。第二个是脉冲宽度。

第二个函数：该函数两个参数，第一个是通道，也就是具体是哪一个舵机。第二个是该舵机旋转的角度。设置为90°就说明舵机处于正中间的位置。

def set_servo_pulse(channel, pulse):
    pulse_length = 1000000    # 1,000,000 us per second
    pulse_length //= 60       # 60 Hz
    print('{0}us per period'.format(pulse_length))
    pulse_length //= 4096     # 12 bits of resolution
    print('{0}us per bit'.format(pulse_length))
    pulse *= 1000
    pulse //= pulse_length
    pwm.set_pwm(channel, 0, pulse)

def set_servo_angle(channel,angle):
    angle=4096*((angle*11)+500)/20000
    pwm.set_pwm(channel,0,int(angle))

下面就是设置频率，将频率设置为50hz，固定不变的

pwm.set_pwm_freq(50)

更改舵机旋转的角度。以便于测试使用。

set_servo_angle(4,90)

time.sleep(1)

set_servo_angle(5,90)

time.sleep(1)