1参考[完全经验法、等幅振荡法、衰减曲线法、响应曲线法]

参考

1.1完全经验法

这种方法没有任何定量规律可循，凭借的是工程技术人员对控制系统与控制对象的工作机理、工作环境的熟悉，是一种粗糙的调参方法，一些定性的调参准则如下：

参数整定找最佳，从小到大顺序查
先是比例后积分，最后再把微分加
曲线振荡很频繁，比例度盘要放大
曲线漂浮绕大湾，比例度盘往小扳
曲线偏离回复慢，积分时间往下降
曲线波动周期长，积分时间再加长
曲线振荡频率快，先把微分降下来
动差大来波动慢。微分时间应加长
理想曲线两个波，前高后低4比1
一看二调多分析，调节质量不会低

1.2等幅振荡法

步骤：
（1）先将切除PID控制器中的积分与微分作用，取比例增益KC较小值，并投入闭环运行；
（2）将Kc由小到大变化，对应于某一Kc值作小幅度的设定值阶跃响应，直至产生等幅振荡；
（3）设等幅振荡时振荡周期为Tcr、控制器增益Kcr ，再根据控制器类型选择以下PID参数。
在这里插入图片描述

1.3衰减曲线法

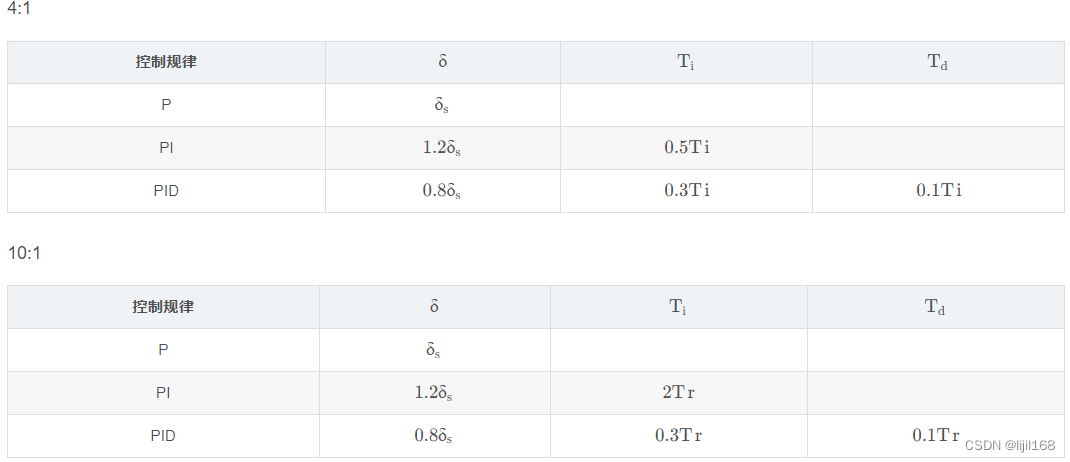
（1）先把积分时间放至最大，微分时间放至零，使控制系统运行，比例度放至较大的适当值，“纯P降低比例度”，就是使控制系统按纯比例作用的方式投入运行。然后慢慢地减少比例度，观察调节器的输出及控制过程的波动情况，直到找出4:1的衰减过程为止。这一过程就是“找到衰减4:1”。
（2）对有些控制对象，用4:1的衰减比感觉振荡过强时，这时可采用10:1的衰减比。但这时要测量衰减周期是很困难的，可采取测量第一个波峰的上升时间Tr，其操作步骤同上。
（3）根据衰减比例度s和衰减周期Ts、Tr按表1进行计算，求出各参数值。
在这里插入图片描述

1.4响应曲线法

响应曲线法PID参数整定步骤：
（1）在手动状态下，改变控制器输出（通常采用阶跃变化），记录被控变量的响应曲线；
（2）由开环响应曲线获得单位阶跃响应曲线，并求取 “广义对象”的近似模型与模型参数；
（3）根据控制器类型与对象模型，选择PID参数并投入闭环运行。在运行过程中，可对增益作调整。
由于广义对象的响应曲线可以用“一阶+纯滞后”来近似，所以，如下Ziegler-Nichols参数整定方法可以使用
在这里插入图片描述

2响应曲线法PID整定示例

根据带有时滞环节的一阶近似模型的阶跃响应来整定PID，如果单位阶跃响应曲线为S形曲线，则可用此法。
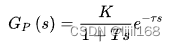
在这里插入图片描述
假设系统 T=60,tao=80,单位阶跃响应模型为：

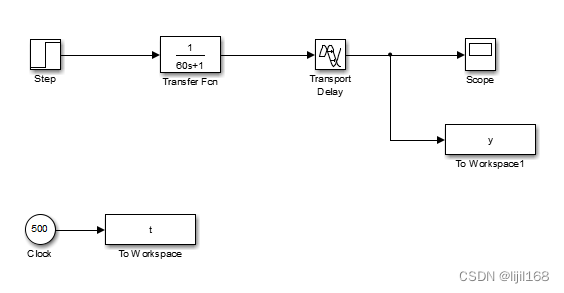
绘图：

close all;
figure(1);
plot(t,y,'k','linewidth',2);
xlabel('time(s)');ylabel('y');

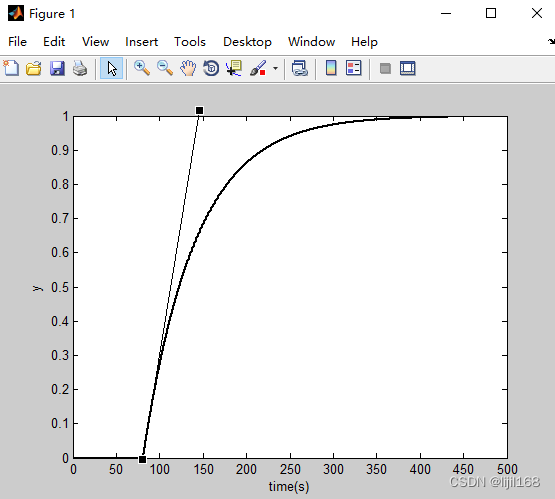
在这里插入图片描述
测得tao=80,T=60
计算增益K=dy/(ymax-ymin):du/(umax-umin)=1
Kc=1.2 * 1/K * T/tao=1.2 * 1/1 * 60/80=0.9
Ti=2.2 * tao=2.2 * 80=176
Td=0.5 * tao=0.5 * 80=40

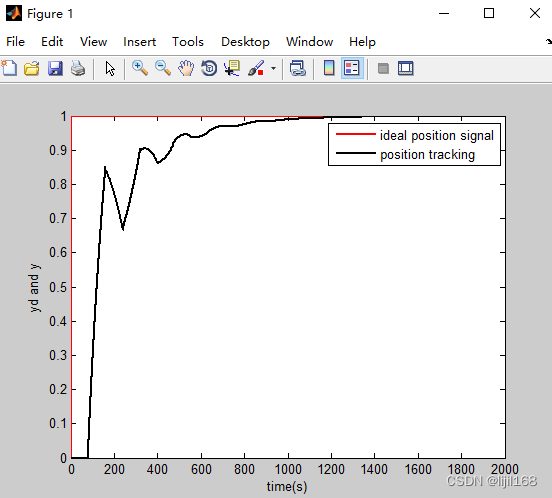
连续PID控制仿真：
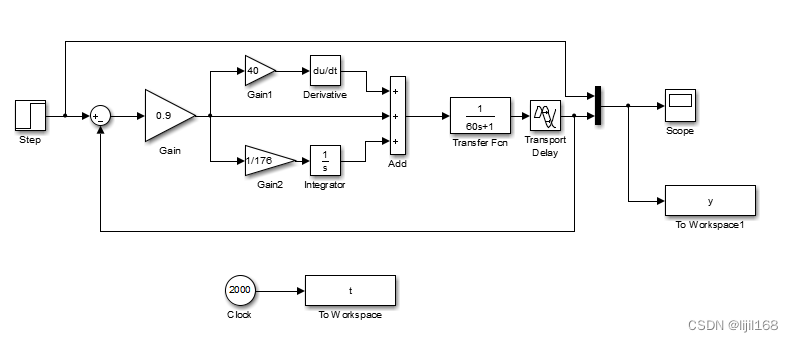
在这里插入图片描述
绘图：

close all;
figure(1);
plot(t,y(:,1),'r',t,y(:,2),'k','linewidth',2);
xlabel('time(s)');ylabel('yd and y');
legend('ideal position signal','position tracking');