这是多元微积分的高潮部分。

对于一个函数F(x,y)=0，我们想知道是否可以用y=f(x)来表示它。

或者说，在不求出y=f(x)表达式的情况下，我们能拿到一些额外信息：

比如f'(x)等。

这就是隐函数定理。

 这个很有意思，根据隐函数定理，我们可以把一个F(x1,x2,...xm)=0的函数改成

xm=f(x1,x2,...xm-1)的函数。

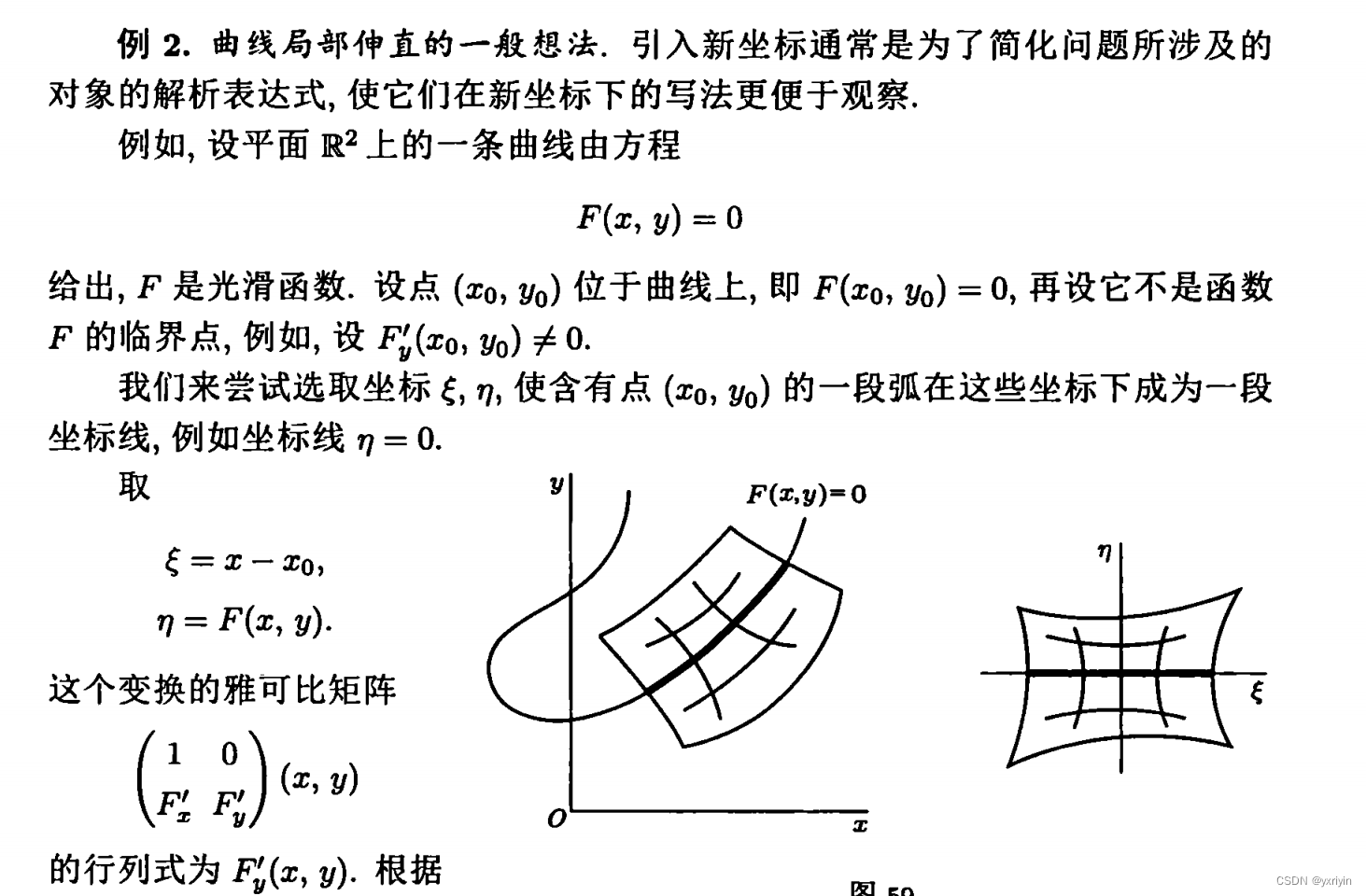
切平面方程是一个很重要的方程，对于一个曲面F,它的切平面方程就是上面写的这个。可以这么去记忆,从全微分方程出发：

把换成对应的(x-x0)之类即可，就得到第一种显式的切平面方程，这里的显式指z=f(x,y)是一个显式方程。

如果它是一个隐式方程，那么根据公式，可以得到一个对称形式的切平面方程：

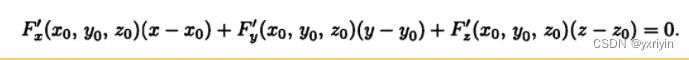
后面还需要继续推广到多维情况，这里先注意下。

这里要注意，梯度和切平面是相互垂直的，同时，也可以认为它和函数F的等值面正交。等值面可以这么理解，首先我们熟悉的是F(x)=0,我们改变右边的值，相当于不改变形状的情况下进行图形变换，考虑一个圆，改变右边的值相当于对这个圆做缩放。

证明过于复杂，哪天需要的时候我再重新整理，大部分情况下感觉记录一个结论就够用了。

 这里引入了微分同胚的概念。虽然这里主要讲双射，同时f和f的逆都是一阶可微的，但实际应该还是主要靠反函数定理来使用：

重点是x0点的微分可逆。 

 反函数定理是线性代数里面坐标变换的局部形式。微分可逆对应着线性变换矩阵可逆。如果说一个映射是光滑的，那么在一个点的小邻域内，它的性质和它的微分基本一样。

这句话我理解了很久，最后请教了chatgpt.

应该是这个意思：微分描述的是在这个小邻域内的差量，重点是通过这个差量：