目录
3.2.6 选择问题
分析过程:
解法一:
算法代码:
【单组数据】
【多组数据】
运行结果:
解法二
代码:
运行结果:
解法三:
3.2.6 选择问题
输入有多组测试例。
对每一个测试例有2行,第一行是整数n和k(1≤k<n≤1000),第二行是n个整数。
第k小的元素。
| 输入样例 | 输出样例 |
| 5 2 3 9 4 1 6 7 3 4 59 7 23 61 55 46 | 3 23 |
分析过程:
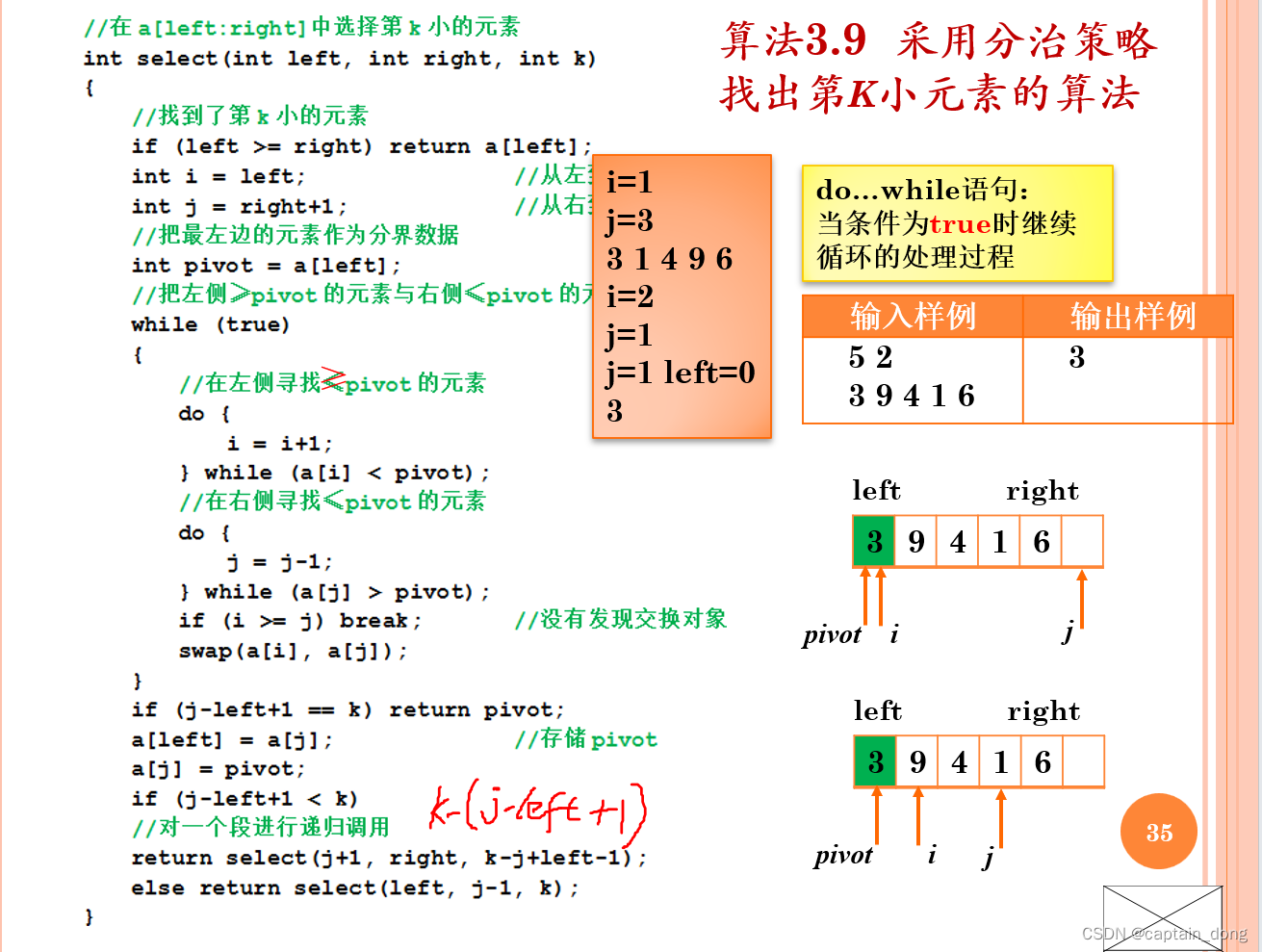
¢ 一种简单的解决方法就是对全部数据进行排序,于是得到问题的解。l 但即使用较好的排序方法,算法的复杂性也为 n log n 。¢ 快速排序算法是分治策略的典型应用,不过不是对问题进行等份分解(二分法),而是通过分界数据(支点)将问题分解成独立的子问题。
¢ 首先选 第一个数 作为分界数据,将比它 小 的数据存储在它的 左边 ,比它 大 的数据存储在它的 右边 ,它存储在左、右两个子集之间。这样左、右子集就是原问题分解后的独立子问题。l 再用同样的方法,继续解决这些子问题,直到每个子集只有一个数据,就完成了全部数据的排序工作。
¢ 利用 快速排序算法的思想,来解决选择问题。l 记 一趟快速排序后,分解出 左子集 中元素个数为 nleft ,则选择问题可能是以下几种情况之一:① nleft = k ﹣ 1,则分界数据就是选择问题的答案。② nleft > k ﹣ 1 ,则选择问题的答案继续在左子集中找 ,
问题规模变小了。③ nleft < k ﹣ 1 ,则选择问题的答案继续在右子集中找 ,
问题 变为选择 第 k- nleft -1 小的数,问题的 规模变 小了。
| 输入样例 | 输出样例 |
| 5 2 3 9 4 1 6 | 3 |
| 1 | 3 | 9 | 4 | 6 |
此算法在最坏情况时间复杂度为 O(n 2 ) ,此时 nleft 总是为 0 ,左子集为空,即第 k 小元素总是位于 right 子集中。平均时间复杂度为 O( n ) 。
解法一:
算法代码:
【单组数据】
#include<iostream>
#include<algorithm>
using namespace std;
const int NUM = 1001;
int a[NUM];
int select(int left,int right,int k){
//找到了第k小色元素
if (left >= right)
return a[left];
int i = left;//从左到右的指针
int j = right;//从右到左的指针
int pivot = a[left];//把最左边的元素作为分界数据
while (true)
{
//寻找左边大于pivot的数
do {
i++;
} while (a[i]<pivot);
//寻找右边小于pivot的数
do {
j--;
} while (a[j] > pivot);
if (i >= j)
break;//没有发现交换对象
swap(a[i], a[j]);
}
if (j - left + 1 == k)
return pivot;
a[left] = a[j];
a[j] = pivot;
if (j - left + 1 < k)
return select(j + 1, right, k - (j - left + 1));
else
return select(left, j - 1, k);
}
int main() {
int n, k;
cin >> n >> k;
for (int i = 0; i < n; i++) {
cin >> a[i];
}
cout<<select(0, n - 1, k);
return 0;
}【多组数据】
#include<iostream>
#include<algorithm>
using namespace std;
const int NUM = 1001;
int a[NUM];
int select(int left, int right, int k) {
//找到了第k小色元素
if (left >= right)
return a[left];
int i = left;//从左到右的指针
int j = right;//从右到左的指针
int pivot = a[left];//把最左边的元素作为分界数据
while (true)
{
//寻找左边大于pivot的数
do {
i=i+1;
} while (a[i] < pivot);
//寻找右边小于pivot的数
do {
j=j-1;
} while (a[j] > pivot);
if (i >= j)
break;//没有发现交换对象
swap(a[i], a[j]);
}
if (j - left + 1 == k)
return pivot;
//存储pivot
a[left] = a[j];
a[j] = pivot;
if (j - left + 1 < k)
return select(j + 1, right, k - (j - left + 1));
else
return select(left, j - 1, k);
}
int main() {
int n, k;
while (cin >> n >> k && n != 0 && k != 0) {
for (int i = 0; i < n; i++) {
cin >> a[i];
}
cout << select(0, n - 1, k) << endl;
}
return 0;
}
这段代码实现了选择问题中的查找第 k 小元素的算法,该算法通过快速选取法(QuickSelect)实现,基本思路为利用快速排序的部分思路进行枢轴(pivot)的划分,缩小问题规模,最终得到第 k 小的元素。
具体来说, select 函数的流程如下:
- 确定枢轴,默认选取序列中的第一个元素 a[left] 作为枢轴。
- 初始化 i = left 和 j = right 两个指针,从两端向中间扫描,直至 i >= j 停止扫描。
- 在扫描过程中,不断移动指针 i 和 j,使 a[i] < pivot 且 a[j] > pivot,然后交换 a[i] 和 a[j] 的值,直到 i >= j 停止。
- 将枢轴和 a[j] 位置的元素互换,将 j - left + 1 的长度作为枢轴左边元素个数计算。
- 如果 k 等于枢轴左边元素个数,则返回枢轴的值。
- 如果 k 小于枢轴左边元素个数,则递归地在左半边序列里选择第 k 小元素。
- 如果 k 大于枢轴左边元素个数,则递归地在右半边序列里选择第 k - (j - left + 1) 小元素。
例如,对于序列 {3, 5, 1, 6, 4, 2},查找第 3 小的元素,在 select(0, 5, 3) 中,首先选择 a[0] = 3 作为枢轴 pivot,然后从两端开始移动指针,扫描过程如下:
[3] 5 1 6 4 2 // i = 1, j = 5 3 [2] 1 6 4 5 // i = 2, j = 4 3 [2 1] 6 4 5 // i = 3, j = 4 3 [2 1] 4 6 5 // i = 3, j = 3 3 [2 1] 4 5 6 // i = 3, j = 2 3 2 [1 4] 5 6 // i = 4, j = 1 3 2 [1 4] 5 6 // i = 4, j = 1, 结束扫描从上表可以看出,最终将枢轴和 a[j] 位置的元素互换,得到序列 {1, 2, 3, 6, 4, 5},此时第 3 小的元素 为 3,返回结果。
a[left] = a[j]; a[j] = pivot;在这段代码中,
a[left] = a[j]的作用是将枢轴的值(即最左边的元素)与当前分界点j所在位置的元素交换。而a[j] = pivot则是将原来的枢轴值(即最左边的元素)赋给当前分界点j所在位置,保证了左右两个子序列仍然是以枢轴值为分界的。这样做的原因是,选择算法在进行一轮快速排序后会得到分界点
j的位置,也就是说,在分界点左边的所有元素都小于枢轴值,而在右边的所有元素都大于它。但是此时枢轴已经不在最左边,而是位于分界点处,因此需要将枢轴的位置与分界点所在位置进行交换,以便在递归处理子区间时能够正确地处理左右子序列。总之,
a[left] = a[j]和a[j] = pivot这两行代码可以帮助我们维护所需的元素分界点,确保选择算法能够正确地返回第 k 小的元素。
这段代码是一个经典的算法——快速选择,用于在一个无序数组中找到第 k 小的元素。它的改进之处可能包括以下几个方面:
随机选择枢轴 - 快速选择算法实际上是一种快速排序的变体,它通过将数组分为两个部分来寻找第 k 小的元素。在选择枢轴时,可以考虑随机选择一个位置而不是一直使用最左边的元素。这样能够减少最坏情况的出现概率,提高算法的效率。
三数中值分割 - 在选择枢轴时,可以考虑多取几个数并找到这些数的中位数作为枢轴值。这样能够更好地均衡左右子序列的大小,减少递归次数。
循环选择 - 如果数组很大,递归选择可能会耗费大量的时间和空间。因此,可以考虑使用循环选择算法来代替递归算法,从而提高算法的效率。
利用线性时间选择算法 - 在某些情况下,我们需要在无序数组中查找第 k 小的元素,并且这个元素的规模非常大,超出了基于比较排序的算法的时间复杂度下界。这时可以使用线性时间选择算法来解决这个问题,它的时间复杂度为 O(n)。
需要指出的是,以上提到的改进并不是一定都要实现,具体要看具体情况,找到适合自己问题的最优解即可。
运行结果:

解法二
为了解决输入数据不随机排列以及比较元素大小时出现的问题,可以对快速选择算法进行以下改进:
- 在每次递归之前,随机选取一个元素作为枢轴点,确保元素的选择是随机的。
- 比较元素大小时使用 <= 和 >=,以处理数组中有重复元素的情况。
- 使用插入排序等排序算法来处理小数据集,避免 QuickSelect 算法退化成 O(n^2)。
下面是改进后的代码实现:
-
代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int NUM = 1001;
int a[NUM];
// 插入排序,用于处理小数据集
void insertionSort(int a[], int start, int end) {
for (int i = start + 1; i <= end; i++) {
int key = a[i];
int j = i - 1;
while (j >= start && a[j] > key) {
a[j + 1] = a[j];
j--;
}
a[j + 1] = key;
}
}
int quickSelect(int a[], int left, int right, int k) {
if (right - left + 1 <= 5) {
insertionSort(a, left, right);
return a[left + k - 1];
}
// 随机选择枢轴点
int pivotIndex = rand() % (right - left + 1) + left;
int pivot = a[pivotIndex];
swap(a[pivotIndex], a[right]);
int i = left - 1;
for (int j = left; j < right; j++) {
if (a[j] <= pivot) {
i++;
swap(a[i], a[j]);
}
}
swap(a[i + 1], a[right]);
int index = i + 1 - left + 1;
if (index == k) {
return a[i + 1];
}
else if (index > k) {
return quickSelect(a, left, i, k);
}
else {
return quickSelect(a, i + 2, right, k - index);
}
}
int main() {
int n, k;
while (cin >> n >> k && n != 0 && k != 0) {
for (int i = 0; i < n; i++) {
cin >> a[i];
}
cout << quickSelect(a, 0, n - 1, k) << endl;
}
return 0;
}
这段代码实现了快速选择算法,用于查找数组中第 k 小的元素。具体过程如下:
- 读入数据,包括数组大小 n 和要查找的第 k 小的元素。
- 读入 n 个整数,表示要查找的数组。
- 调用 quickSelect 函数查找数组中第 k 小的元素,并打印结果。
- 重复步骤 1~3,直到读入的 n 和 k 均为 0 为止。
在 quickSelect 函数中,首先判断当前处理的数据集是否已经很小(比如小于等于 5),如果是,则使用插入排序来处理。这是因为插入排序对于小数据集的效率更高。
如果数据集很大,则随机选取一个枢轴点,将比枢轴点小的元素放在数组左边,比枢轴点大的元素放在数组右边。此时,枢轴点就是整个数组中的第 index 小元素(index 是枢轴点的位置)。通过比较 index 和 k 的大小关系,可以判断第 k 小元素在数组的哪一侧,并递归处理该侧的数据集,直到找到第 k 小的元素。
值得注意的是,为了避免算法退化成 O(n^2),每次递归前都需要随机选择枢轴点,保证算法的随机性。另外,在比较元素大小时,使用了 <= 和 >=,以处理数组中有重复元素的情况。
-
运行结果:
解法三:
C++:分治算法之选择问题的选择第k小元素问题
用 C++ 设计分治算法解决选择问题中的选择第 k 小元素问题。
首先,对于一个无序数组来说,如果想要找到其中第 k 小的元素,可以使用快速选择算法(QuickSelect)进行处理。快速选择算法的基本思路是选取数组中的一个主元,将数组划分为两个部分,并根据主元在数组中的位置关系,决定继续处理数组的哪一部分。通过每次划分将待查找的第 k 小元素所在的区间不断缩小,最终得到结果。
然而,在实际应用中,数据量很大时,快速选择算法的效率可能会受到影响。这时可以使用分治算法来解决问题。分治算法是一种将问题分成若干个子问题处理的思想,通过将原问题分解为多个规模较小的子问题并逐个解决,最终将子问题的解组合起来得到原问题的解。
具体来说,对于选择第 k 小元素的问题,可以利用分治算法的思想将数组按照主元划分为两个部分,并根据主元在数组中的位置关系,决定继续处理数组的哪一部分。每次处理只需要考虑一个子问题,这样就不需要对整个数组进行排序,从而提高了算法的效率。可以使用递归的方式实现分治算法解决选择问题中的选择第 k 小元素问题。
下面是 C++ 代码示例:
int quickSelect(vector<int>& nums, int left, int right, int k) {
if (left == right) {// 只有一个元素
return nums[left];
}
// 选取一个主元
int pivotIndex = rand() % (right - left + 1) + left;
int pivot = nums[pivotIndex];
// 将数组按照主元划分为两部分
swap(nums[pivotIndex], nums[right]);
int i = left - 1;// i 表示左数组的右边界位置
for (int j = left; j <= right; j++) {
if (nums[j] < pivot) {
i++;
swap(nums[i], nums[j]);
}
}
swap(nums[i+1], nums[right]);
i++;
// 根据主元在数组中的位置关系决定继续处理左/右子问题
if (k == i - left + 1) {
return nums[i];
} else if (k < i - left + 1) {
return quickSelect(nums, left, i-1, k);
} else {
return quickSelect(nums, i+1, right, k - (i - left + 1));
}
}
int kthSmallest(vector<int>& nums, int k) {
return quickSelect(nums, 0, nums.size()-1, k);
}
以上代码中的
quickSelect函数为快速选择算法的实现,kthSmallest函数则是使用分治算法解决选择问题中的选择第 k 小元素问题的实现。函数的参数含义如下:
nums:待查找第 k 小元素的数组;left:当前处理区间的左边界;right:当前处理区间的右边界;k:目标元素的排名。



![P1915 [NOI2010] 成长快乐](https://img-blog.csdnimg.cn/a164f63cd9ac4a71acf90885c53b1857.png)