专注系列化、高质量的R语言教程
推文索引 | 联系小编 | 付费合集
本篇来介绍tobit模型,使用的工具包是VGAM。
library(VGAM)目录如下:
1 Tobit分布
2 tobit模型
3 运行模型
例1
例2
例3
4 其他
1 Tobit分布
tobit模型主要应用于因变量存在删失的情况。以正态分布为例,变量的取值范围理论上应为,但实际取值范围只是某个区间。例如在做调查时,年收入在一定区间范围内需要精确统计,而低于或高于某与水平只笼统归类。
这样删失数据的概率分布相比于正态分布就发生了变化:
概率密度分布:
x <- seq(-4, 4, 0.001)
plot(x, dnorm(x), type = "l", ylab = "概率密度")
lines(x, dtobit(x, Lower = -2, Upper = 2),
col = "orange", lty = "dashed")
abline(v = -2, lty = "dashed")
abline(v = 2, lty = "dashed")
legend(x = "topleft", c("正态分布", "Tobit分布"),
lty = c("solid", "dashed"), col = c("black", "orange"))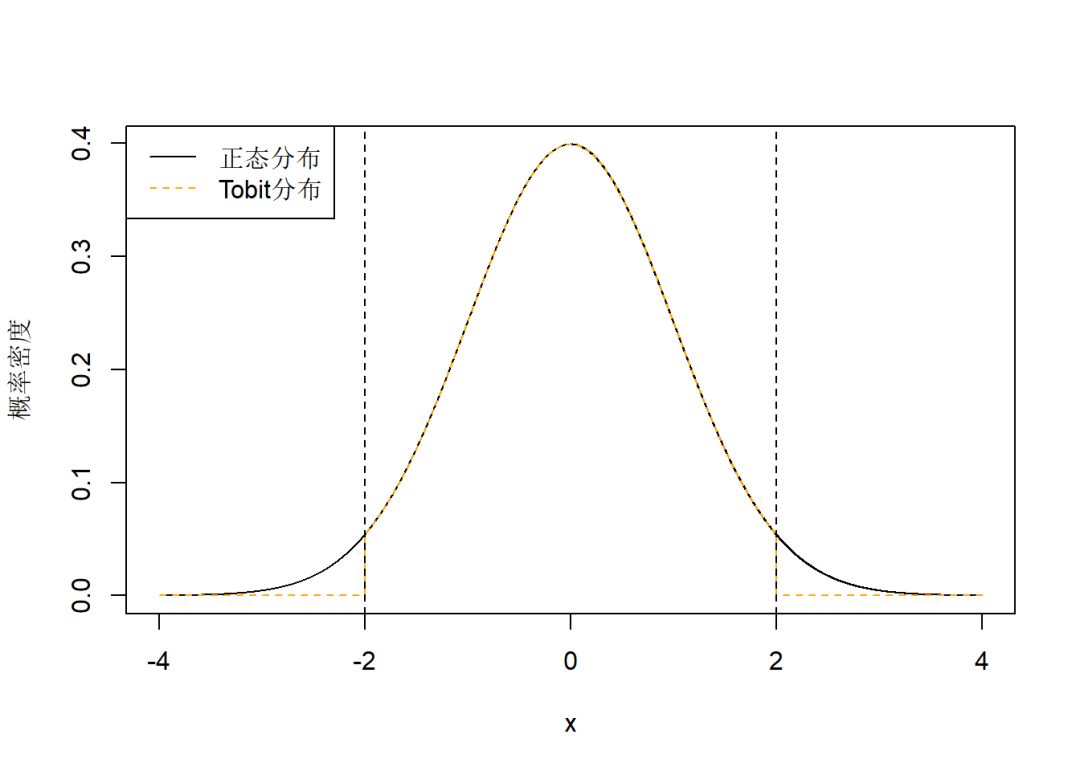
注意:概率密度在区间端值处相比于正态分布并没有变化。
累积概率分布:
plot(x, pnorm(x), type = "l", ylab = "累积密度")
lines(x, ptobit(x, Lower = -2, Upper = 2),
col = "orange", lty = "dashed")
abline(v = -2, lty = "dashed")
abline(v = 2, lty = "dashed")
legend(x = "topleft", c("正态分布", "Tobit分布"),
lty = c("solid", "dashed"), col = c("black", "orange"))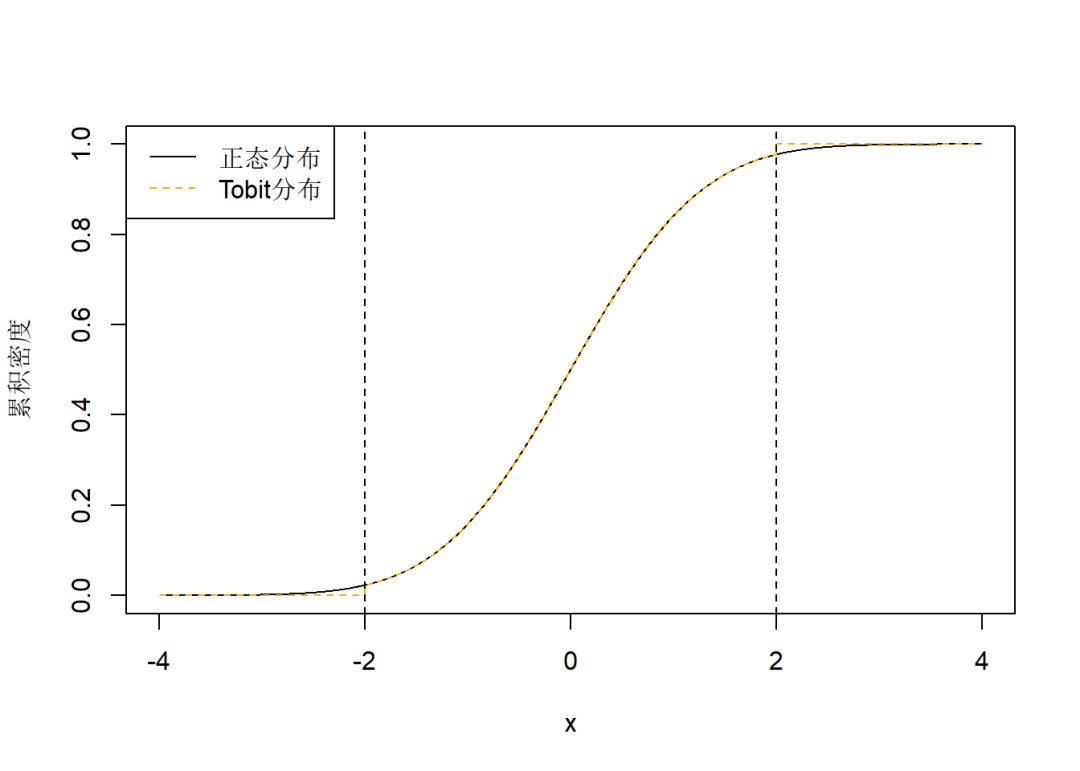
上面代码中使用的dtobit()、ptobit()函数是分别计算Tobit分布的概率密度和累积密度的。
VGAM工具包中关于Tobit分布的系列函数:
dtobit(x, mean = 0, sd = 1, Lower = 0, Upper = Inf, log = FALSE)
ptobit(q, mean = 0, sd = 1, Lower = 0, Upper = Inf,
lower.tail = TRUE, log.p = FALSE)
qtobit(p, mean = 0, sd = 1, Lower = 0, Upper = Inf,
lower.tail = TRUE, log.p = FALSE)
rtobit(n, mean = 0, sd = 1, Lower = 0, Upper = Inf)
Lower和Upper参数分别表示区间的最小值和最大值。
2 tobit模型
以线性回归为例,如果因变量是删失数据,那么可以使用对应的tobit模型:
其中服从独立的正态分布。假设区间上、下限分别为 = a、 = b,删失数据的处理如下:
下面生成四个样本量为100的示例数据,已知与理论上的数量关系为,真实数据存在随机扰动。
数据y:随机扰动服从正态分布。
set.seed(0501)
nn <- 100
x <- seq(-4, 4, length = nn)
y <- rnorm(nn, mean = 2*x +2)数据y1:随机扰动服从默认的Tobit分布(L = 0,U = ,即下限为0,无上限)。
set.seed(0501)
y1 <- rtobit(nn, mean = 2*x + 2)数据y2:随机扰动服从Tobit分布(L = -2,U = 6)。
set.seed(0501)
y2 <- rtobit(nn, mean = 2*x + 2, Lower = -2,
Upper = 6)数据y3:随机扰动服从Tobit分布,但每个样本的上、下限不同(例如调查数据来自不同调查组)。
set.seed(0501)
lower <- rnorm(nn, -2, 0.5) ## 下限
upper <- rnorm(nn, 6, 0.5) ## 上限
y3 <- rtobit(nn, mean = 2*x + 2, Lower = lower,
Upper = upper)各示例数据的散点图:
par(mfrow = c(2,2), plt = c(0.1, 0.9, 0.15, 0.9),
mgp = c(1.2,0.3,0), pch = 20,
las = 1, tck = -0.02)
plot(x, y)
plot(x, y1)
plot(x, y2)
plot(x, y3)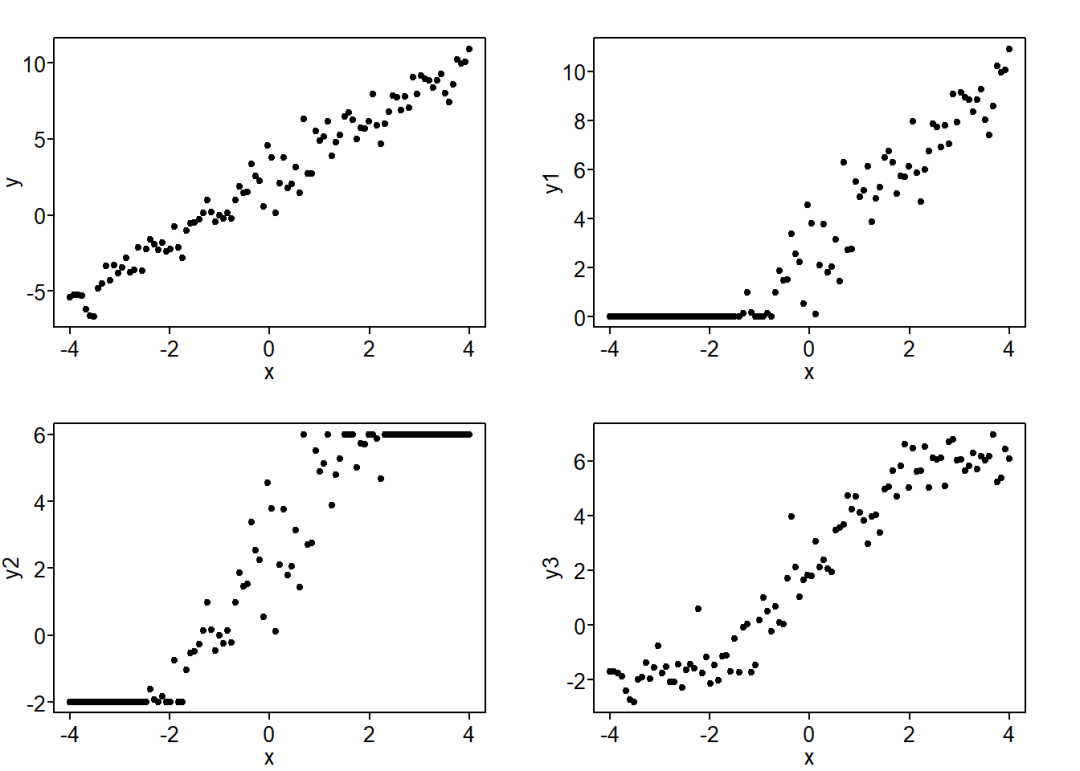




![[stable-diffusion-art] 指北-2 如何为sd提出好的prompt](https://img-blog.csdnimg.cn/4e58f54a484b4e0d891c711cf8ef76c9.png)