v2c是一个Verilog到C的翻译工具。给定一个 在 Verilog 硬件描述语言中寄存器传输级别 （RTL） 硬件电路的描述 （HDL），用于自动翻译Verilog RTL 电路转换为用C语言表示的软件程序。这 软件程序称为软件网表。

一、如何安装

1.下载二进制文件

我们为 Linux 分发 v2c 的预编译静态二进制文件系统
下载二进制文件

2.基准测试

下载基准测试
我们在Verilog中分发了几个基准测试，并且 ANSI-C 用于属性验证、等效性检查和仿真。

二、如何使用

v2c的应用

描述

v2c主要用于我们的硬件属性验证 用于将 Verilog RTL 中给出的硬件电路转换为的工具流程 C语言的软件程序。RTL电路在中的表示 软件语言使我们能够利用一系列软件验证 包括抽象解释和路径符号执行在内的技术 从未应用于 RTL 验证。 也可用于硬件/软件协同验证， 等价性检查和模拟生成的 C 程序。

工具流程

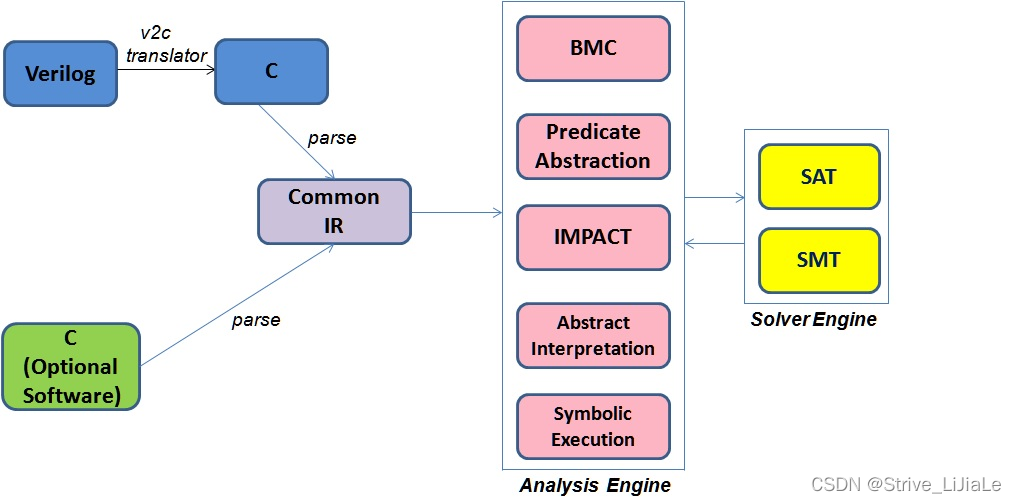
使用 v2c 转换器的工作示例

以下示例说明了 Verilog 到 C 的转换 使用工具。设计包含顺序 和组合逻辑，过程块，阻塞和 非阻塞分配和多个模块层次结构。这 左侧的代码片段给出了Verilog RTL设计和 右侧的代码片段给出了 C 程序。

              Verilog                          C 
------------------------------ 	 ------------------------------
module top(Din,En,CLK,Dout);       struct s_ff {
wire cs; reg ns;                   _Bool q;
input CLK, Din, En;                } sff;
output Dout;                       struct s_en { 
                                    _Bool ns; 
assign Dout = cs;                   struct s_ff sff;
always @(Din or cs or En)          } sen; 
begin                               
if (En)                            _Bool ff(_Bool CLK, _Bool Din, 
ns = Din;                                   _Bool *Dout) { 
else                                 _Bool qold;
ns = cs;                             qold = sen.sff.q; 
end                                  sen.sff.q = Din;
ff ff1(ns,CLK,cs);                   *Dout = qold;
endmodule                            return; 
                                   }
module ff(Din, CLK, Dout);         void top(_Bool CLK, _Bool Din,
input Din, CLK;                     _Bool En, _Bool *Dout) { 
output Dout;                         _Bool cs;
                                     if(En) sen.ns = Din;
reg q;                               else sen.ns = cs;
assign Dout = q;                     ff(CLK,sen.ns,&cs);
always @(posedge CLK)                *Dout = cs;
q <= Din;                          }
endmodule                          int main() {
                                    _Bool CLK,En,Din,Dout; 
                                    while(1) {  
                                     Din = nondet_bool();
                                     En = nondet_bool();
                                     top(CLK,Din,En,&Dout);
                                    }
                                    return;
                                   }

三、注意事项

情形一：拼接：{4{x}}

转换结果：生成错误，乱码，不认识
解决：将简化操作展开：{x，x，x，x}

经测试，位选择拼接也可以{a[0],…}

情形1-1 y&{x，x，x，x}

单独使用{x，x，x，x}，可以正常转换，但再进行&操作，会转换成逻辑&&

情形1-2 y&{x，x，x，x}&z

此时会将{x，x，x，x}转换为CONCATENATION（）
位运算正常，并没有转换成逻辑运算&&

由此可见：{x,x,x,x}为最小拼接单位

情形二（不考虑~a[0]运算）：位选择表达式a[0]的连续&操作

转换结果：会保留位选择表达式a[0]

解决：拆分为两个最小单元 进行 位选择&操作 ，赋值给非位选择表达式
由此可见：包含位选择a[0]时，不能进行连续&运行，将结果赋给非位选择变量

情形三（不考虑~a[0]运算）：对情形二解决方案进行扩展

仅有两个位选择表达式&操作时，赋值给位选择表达式
结果：产生符号“-”，经验证，此符号为减号作用，可转换

情形四（考虑~a[0]运算）：左边不进行位选择，但右边位选择后进行取反操作

结果：右边会保留位选择表达式

解决：右边位选择取后反操作和&操作不要同时出现，
法一：取中间变量代替位选择取反表达式（但会出现情形五问题，只能采用方法二）；
法二：取中间变量代替将位操作表达式，然后将此中间变量取反后再进行&操作。

情形五：~取反运算符与单个位选择表达式搭配使用

结果：会忽略掉~
解决：将当个位选择表达式进行取反赋值给中间变量

总结：

1. 左边表达式不可以是位选择
2. 右边表达式位选择不可直接进行“~”操作

由此可见，位选择是主要影响因素
使其不出现位选择，结果显示可以进行连续&操作
所以进一步确定：需要将位选择操作单独用中间变量进行替换后，其他操作可正常转换！！！

总之：{}为最小拼接单元，a[0]为最小位选择单元，都需要使用中间变量替代！

注：一位相与，会等价为逻辑操作。多位相与，还是位操作。