一、题目描述

原题连接： 274. H 指数&275. H 指数 II
题目描述：
给你一个整数数组 citations ，其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。

根据维基百科上 h 指数的定义：h 代表“高引用次数”，一名科研人员的 h指数是指他（她）的（n 篇论文中）总共有 h 篇论文分别被引用了至少 h 次。且其余的 n - h 篇论文每篇被引用次数不超过 h 次。
如果 h 有多种可能的值，h 指数是其中最大的那个。

示例 1：

输入： citations = [3,0,6,1,5]
**输出：**3
解释：给定数组表示研究者总共有 5 篇论文，每篇论文相应的被引用了 3, 0, 6, 1, 5 次。
由于研究者有 3 篇论文每篇至少被引用了 3 次，其余两篇论文每篇被引用不多于 3 次，所以她的 h 指数是 3。

示例 2：

输入： citations = [1,3,1]
输出： 1

提示：
n == citations.length
1 <= n <= 5000
0 <= citations[i] <= 1000

而275题只是在原有的基础上将数组进行升序排序了

二、解题

1、方法1——排序

1.1、思路分析

很明显h是不会超过数组元素个数的，而如果我们将数组进行降序排序之后发现数组的最后一个元素都大于等于数组的元素个数，那么h就为数组长度了：
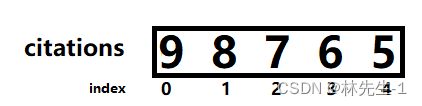
在这里插入图片描述
所以我们可以先将数组进行降序排序，然后将h初始化为0，然后遍历数组，如果citations[i]大于h，那就让h++，而一旦我们发现citations<=h，那就说明citations后面的元素都是小等于h的数字了，这时候我们也就没有在遍历下去的必要了，直接跳出循环即可，例如：
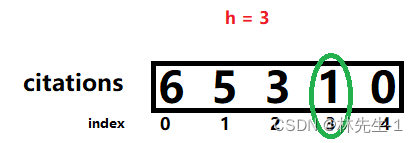
在这里插入图片描述
最后返回h即可。
同样的，这一解法对于275题也是有效的。

1.2、代码实现

有了以上思路，那我们写起代码来也就水到渠成了：

// 先写一个函数，反向比较两个整数的大小
int cmp_int(const void *p1, const void *p2) {
    assert(p1 && p2);
    return *((int*)p2) - *((int*)p1);
}
int hIndex(int* citations, int citationsSize){
    assert(citations);
    // 先对数组进行排序
    qsort(citations, citationsSize, sizeof(int), cmp_int);
    int h = 0;
    int i = 0;
    for (i = 0; i < citationsSize; i++) {
        if (citations[i] > h) {
            h++;
        } else {
            break;
        }
    }
    return h;
}

时间复杂度：O(nlogn)，为数组的长度，时间复杂度主要取决于排序数组的复杂度。
空间复杂度：O(1)，我们只需要用到常数级的额外空间。

1.3、升级到275题的二分法

1.3.1、思路分析

既然275题已经帮我们把数组升序排序好了，那我们就可以考虑使用二分法。
通过上一解法我们可以看出，如果在遍历到citations[i]之前h是一直增加的，那么当遍历到citations[i]时，h的值其实就等于其下标i：
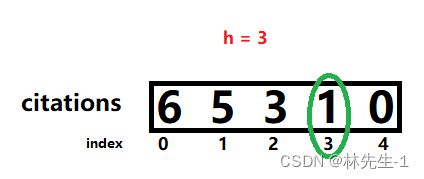
在这里插入图片描述
所以在上一解法中我们其实只需要找到第一个citations[i] <= i的元素即可。
而将这个思路延伸到以升序排序的数组中，其实我们只需要找到第一个大于等于包括它在内的后面的元素个数的元素citations[i]即可，例如：
在这里插入图片描述
这里的元素3是第一个大于等于后面元素个数的元素，所以我们直接返回这个个数即可。
而这个找元素的操作，我们用二分法完成。

1.3.2、代码实现

有了以上思路，那我们写起代码来也就水到渠成了：

int hIndex(int* citations, int citationsSize){
    assert(citations);
    int left = 0;
    int mid = 0;
    int right = citationsSize - 1;
    while (left <= right) {
        if (citations[left] >= citationsSize - left) {
            return citationsSize - left;
        }
        mid = left + (right - left) / 2;
        if (citations[mid] < citationsSize - mid) {
            left = mid + 1;
        } else {
        	// 其他情况我们都让right往左移
            right = mid;
        }
    }
    return 0;
}

时间复杂度：O(longn)，n位数组的长度。
空间复杂度：O(1)，我们只需要用到常数级的额外空间。

2、方法2——计数排序

对于274题，我们其实还可以用计数排序的思路来解题。

2.1、思路分析

因为h不可能大于数组的长度n，所以对于引用次数大于等于n的论文，我们就可以把他算进至少被引用了n次的论文。
所以我们可以额外创建一个长度为n+1的数组counter，其中counter[i]表示被引用了i次的论文的数量。
当我们创建好了数组统计好了数组counter之后，我们就可以逆序遍历数组counter，先将h初始化为0，然后每遍历到一个元素counter[i]就让好加上counter[i]。
因为题目要求我们找到最大的h，所以当我们找到第一个h >= i的元素时就可以直接返回h。
同样的，这个思路对于275题也是适用的。

2.2、代码实现

有了以上思路，那我们写起代码来也就水到渠成了：

int hIndex(int* citations, int citationsSize){
    assert(citations);
    int n = citationsSize;
    // 先创建一个计数数组
    int *counter = (int*)malloc((n + 1) * sizeof(int));
    if (NULL == counter) {
        perror("malloc fail");
        return -1;
    }
    // 对counter进行初始化
    int i = 0;
    for (i = 0; i <= n;i++) {
        counter[i] = 0;
    }
    // 初始化counter数组
    for (i = 0; i < n; i++) {
        if (citations[i] >= n) {
            counter[n]++;
        } else {
            counter[citations[i]]++;
        }
    }
    // 找到h
    int h = 0;
    for (i = n; i >= 0; i--) {
        h += counter[i];
        if (h >= i) {
            return i;
        }
    }
    return 0;
}