级数可视化

news2024/10/5 13:11:18

泰勒级数

数学家们普遍偏爱多项式，如果评选一下高等数学里面最重要的公式，泰勒公式一定榜上有名，泰勒公式的核心思想就是把一个给定的任意函数，展开成多项式的形式，如果是有限项，就像作泰勒多项式，如果是无限项，就叫做泰勒级数，统称为泰勒展开。如果有一种办法能够把一个稀奇古怪的函数进行泰勒展开，很多复杂的问题就会迎刃而解了。

通俗点说，函数泰勒展说的是这样一回事，知道了函数在某个点的值以及在这个点的从一阶到无穷阶的导数，你便有了预测这个函数在某个范围内取值的能力，这样讲有些玄学的味道，似乎根据当前可以预测未来，实际上确实如此，泰勒公式告诉我们任意一小段函数的轨迹不可避免地要规定后来一切时刻的轨迹，世界的进程必然预先决定于它在任意一小段时间里的状态。一叶知秋，一片树叶的掉落背后隐藏的无数的信息，可以用来推断事物未来的发展，高阶导数则是这些信息的载体，它包含了函数未来变化趋势的信息，赋予了泰勒展开预测未来的能力，只是这个预测范围，不同的函数会有所不同。对于性质比较好的函数，例如正/余弦函数，以及指数函数的预测范围无穷大，而对于其他函数，会有一个有限的预测范围。

那么导数是怎么回事呢？就像你观察一个原子内部，发现里面还藏着一个小宇宙一样，在一个曲线空间的点上，开拓出一个新的曲线空间，求高阶导数呢，就是一层层嵌套的曲线空间，直到开拓出一个常数空间，导数才归为0，也就是没有可以挖掘的信息了，不能继续向下开拓。而对于那些可以无穷次开拓的函数曲线来说，由于潜藏着无穷的信息，所以可以预测地的更远一些。

高等数学中的泰勒公式是以两个定理的形式给出的：

泰勒中值定理1，如果函数f(x)在x_0处具有n阶导数，那么存在x_0的一个邻域对于该邻域内的任意一个x,有：

$\boldsymbol{f(x)=f(x_0)+f'(x0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+\cdots + \frac{f^n(x_0)}{n!}(x-x_0)^n+o((x-x_0)^n)}$

泰勒中值定理2，如果函数f(x)在x_0的某个邻域U(x_0)内具有(n+1)阶导数，那么对任意x属于U(x_0)，有：

$\boldsymbol{f(x)=f(x_0)+f'(x0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+\cdots + \frac{f^n(x_0)}{n!}(x-x_0)^n+\frac{f^{n+1}(\varepsilon )}{(n+1)!}(x-x_0)^{n+1} \ \ \varepsilon \in (x_0,x)}$

因为 $0!=1$ ，我们可以抽象出通项为：

$\frac{f^m(x-x_0)^m}{m!}$

泰勒公式推导

问题提出，设f(x)在x_0处具有n阶导数，当x在x_0两边摄动时，如果我们能够找到一个关于摄动误差(x-x_0)的n次多项式：

$p_n(x)= a_0 + a_1(x-x_0)+a_2(x-x_0)^2+\cdots + a_n(x-x_0)^n$

来近似表达f(x),要求使得:

$\lim_{x\rightarrow x_0}\frac{p_n(x)-f(x)}{(x-x_0)^n} = 0$

如果两个函数图像非常逼近，则不但它们在 $x_0$ 点要相等，他们在这个点的各阶导数应该也要相同，这样，函数图像才有相同的变化趋势，也就是说：

$\\p_n(x_0)=f(x_0) \\ p'_n(x_0)=f'(x_0) \\ p''_n(x_0)=f''(x_0) \\ \cdots \\ p^{(n)}_n(x_0)=f^{(n)}(x_0) \\$

根据以上等式来确定多项式的系数：

$\\ a_0 = f(x_0) \\ 1\cdot a_1=f'(x_0) \\ 2!\cdot a_2 = f''(x_0) \\ \cdots \\ n!\cdot a_n = f^{(n)}(x_0) \\$

即得：

$a_0=f(x_0), a_1=f'(x_0), a_2=\frac{1}{2!}f''(x_0), \cdots, a_n=\frac{1}{n!}f^{(n)}(x_0)$

代入多项式，即可得到：

$p_n(x)= f(x_0) + f'(x_0)(x-x_0)+\frac{1}{2!}f''(x_0)(x-x_0)^2+\cdots + \frac{1}{n!}f^{(n)}(x_0)(x-x_0)^n$

Geogebra观察泰勒展开

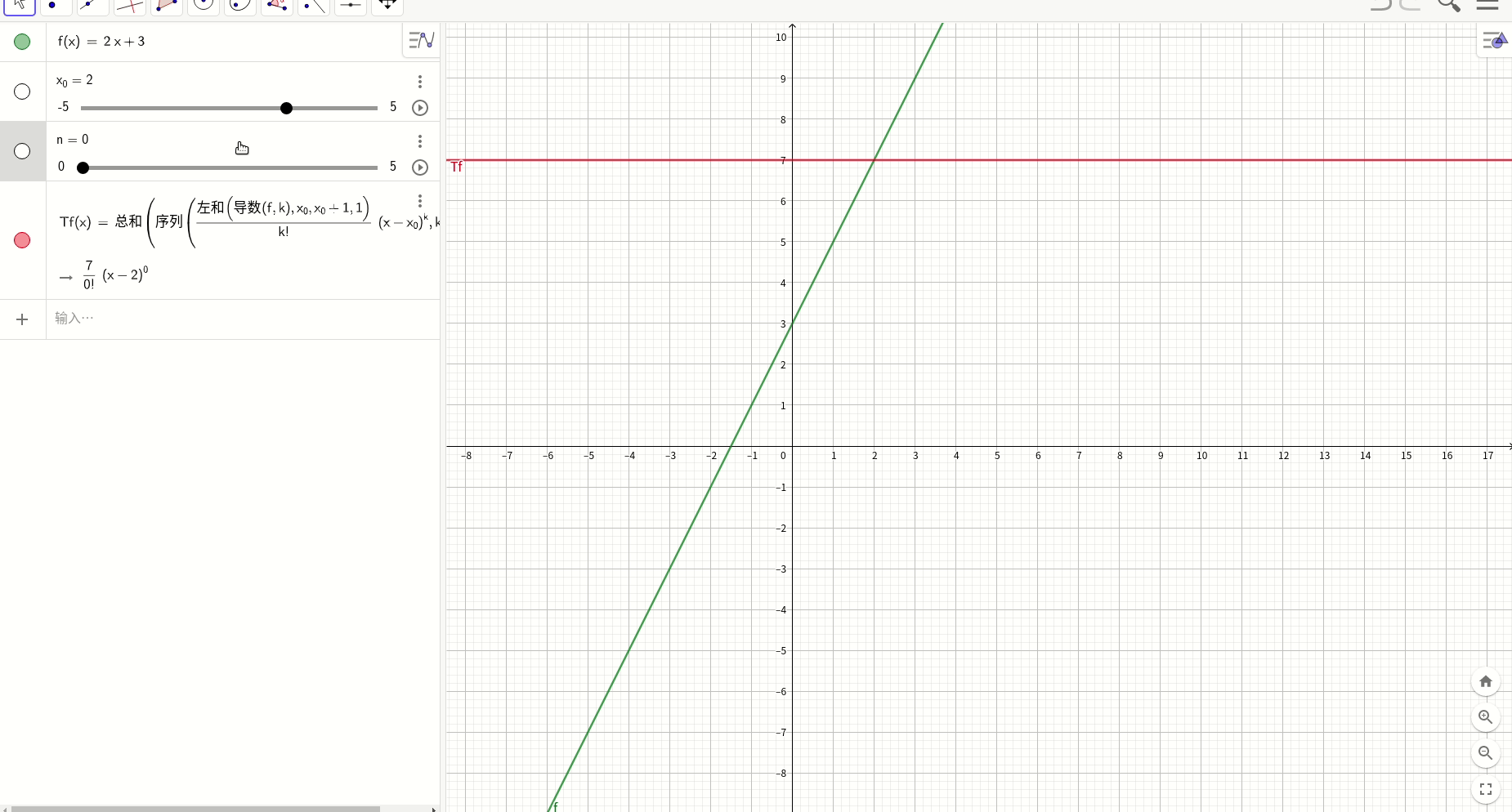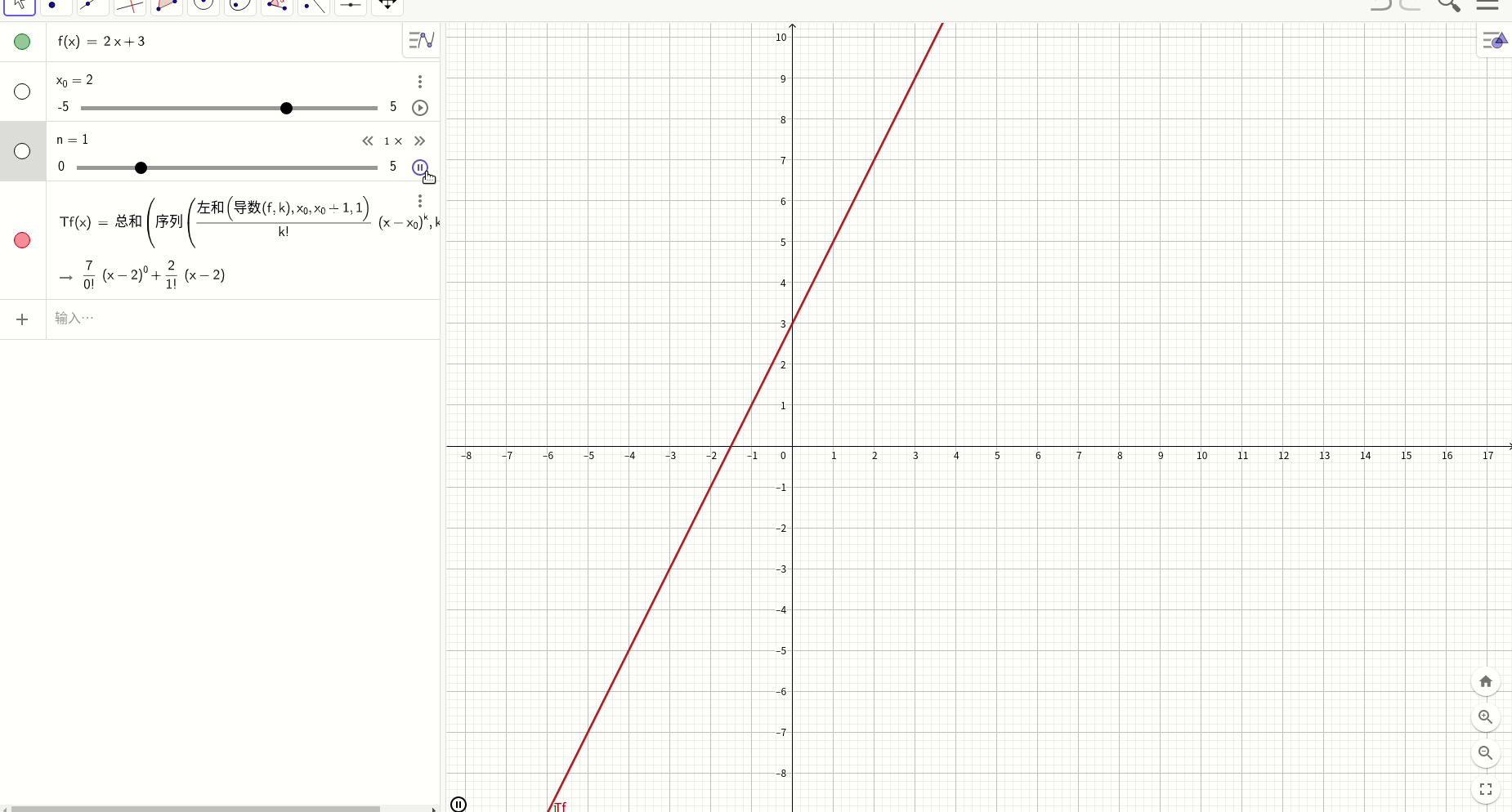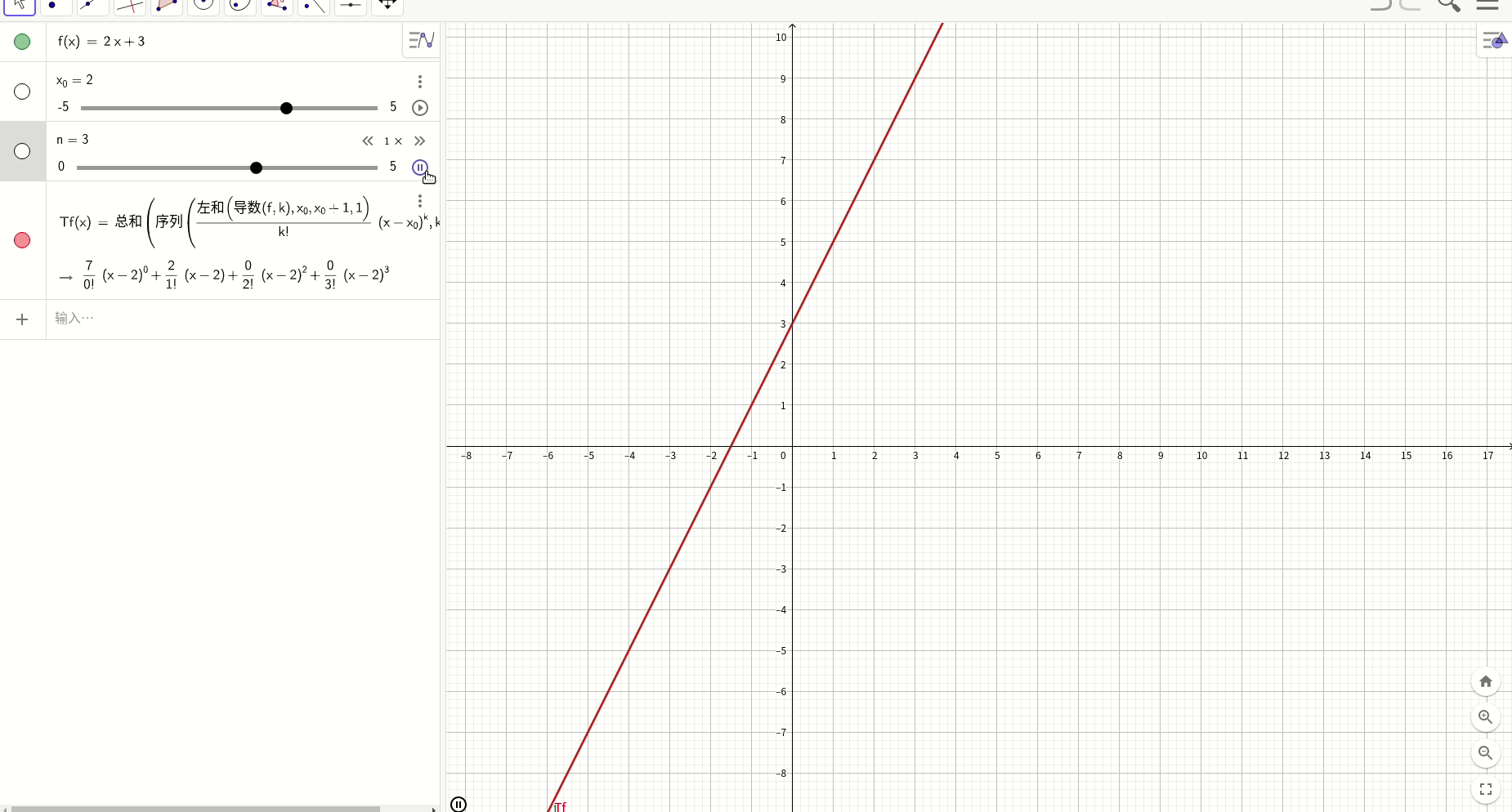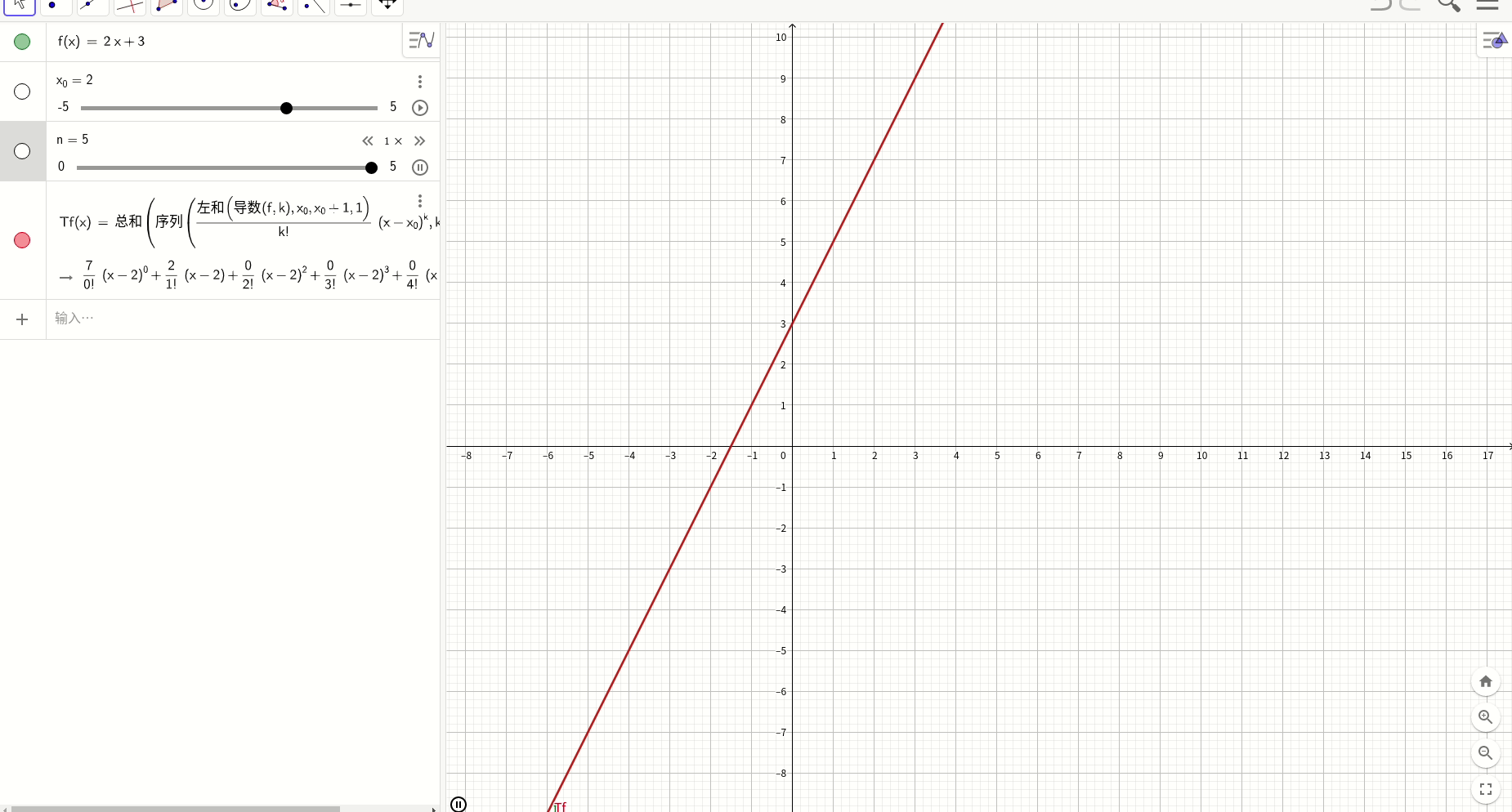
介绍一种用geogebra观察泰勒级数的方法，非常方便，步骤如下：

1.定义级数解析式,比如:

$f(x)=e^x$

2.定义解析零点 $x_0 = 0$

3.定义级数项n.

4.用geogebra sequence函数实现泰勒级数的展开式：

Tf(x) = Sum(Sequence(LeftSum(Derivative(f, k), x_0, x_0 + 1, 1) / k! (x - x_0)^k, k, 0, n))

使用这个工具，分析几个函数的渐近变化趋势。

1。自然指数函数 $y=e^x$

泰勒展开为：

$y=1+\frac{x}{1}+\frac{x^2}{2!}+\cdots + \frac{x^n}{n!}+\cdots$

正弦函数

$sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots+(-1)^{m-1}\frac{x^{2m-1}}{(2m-1)!}+\cdots$

函数 $y=ln(1+x)$

和前面两个函数不同，这个函数是有收敛区间的，图中随着项数逐渐增加，展开式右侧图形不再趋近原函数，而是在原函数上下摆动即可看出来这个特点，实际上，严格的数学证明可以知道，从复平面分析角度，可以证明这个收敛区间是一个圆。

一次函数y=2x+3

高次多项式

$y=x^4-6x^3-3x^2+8x+100$

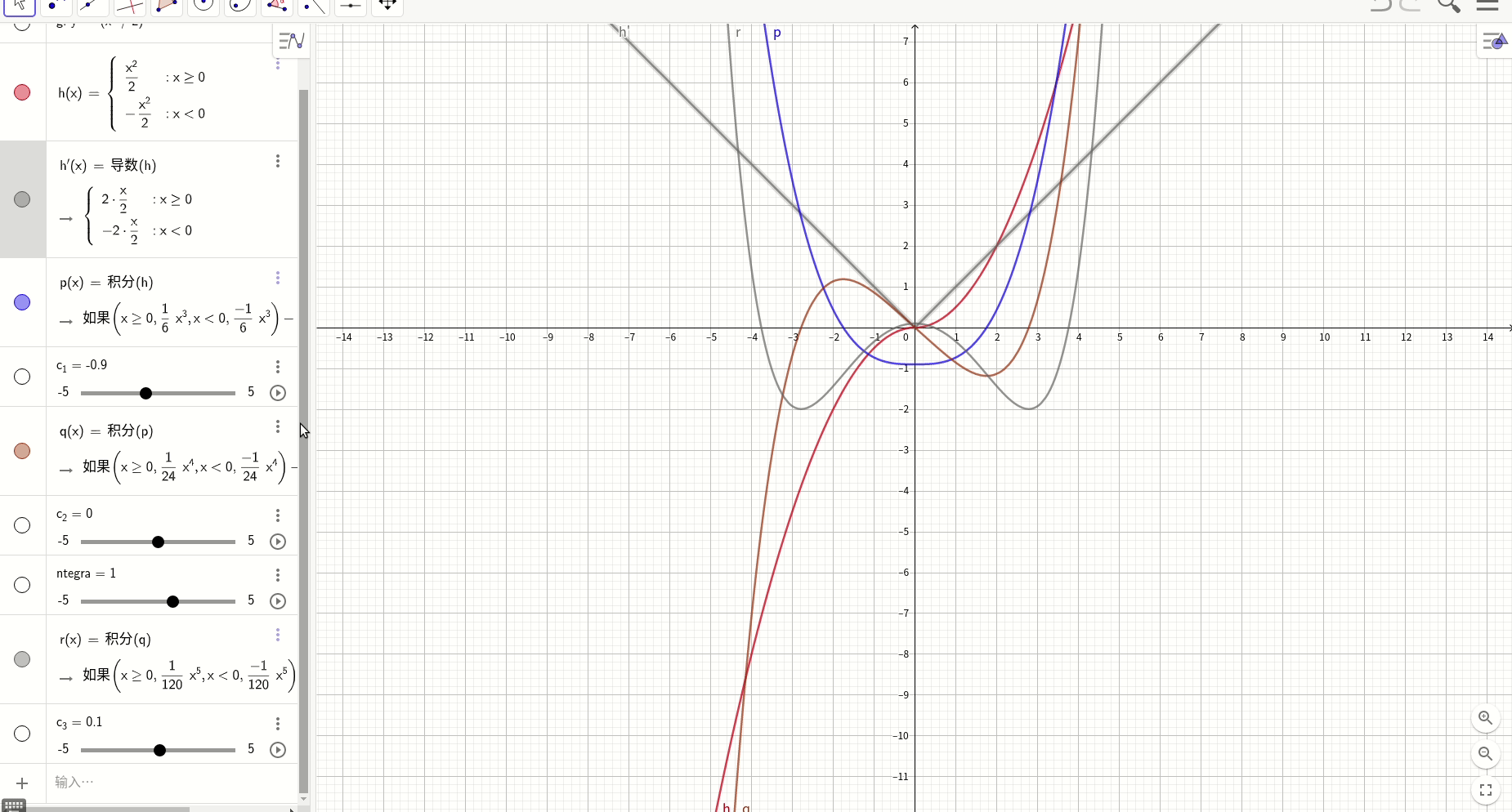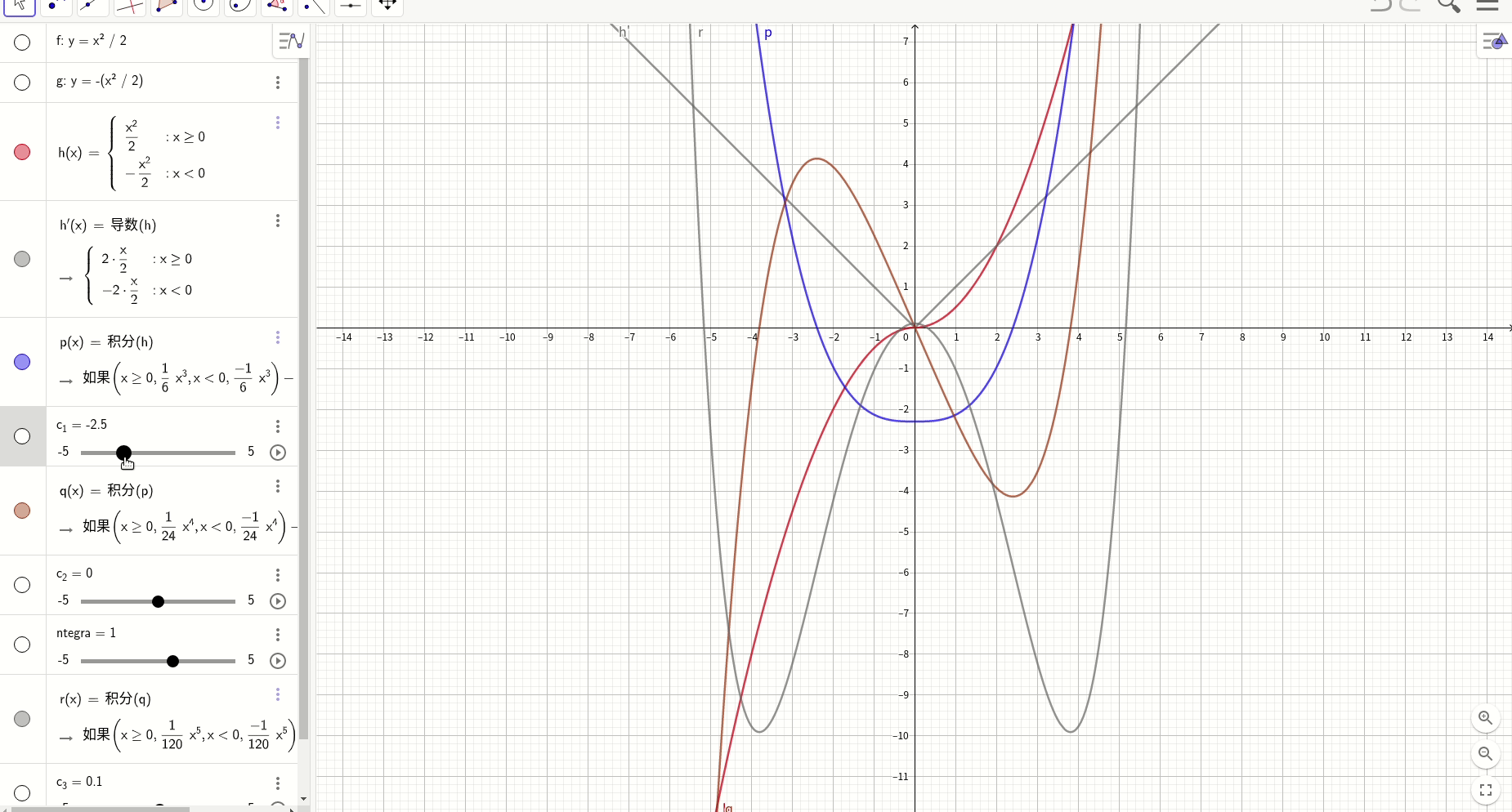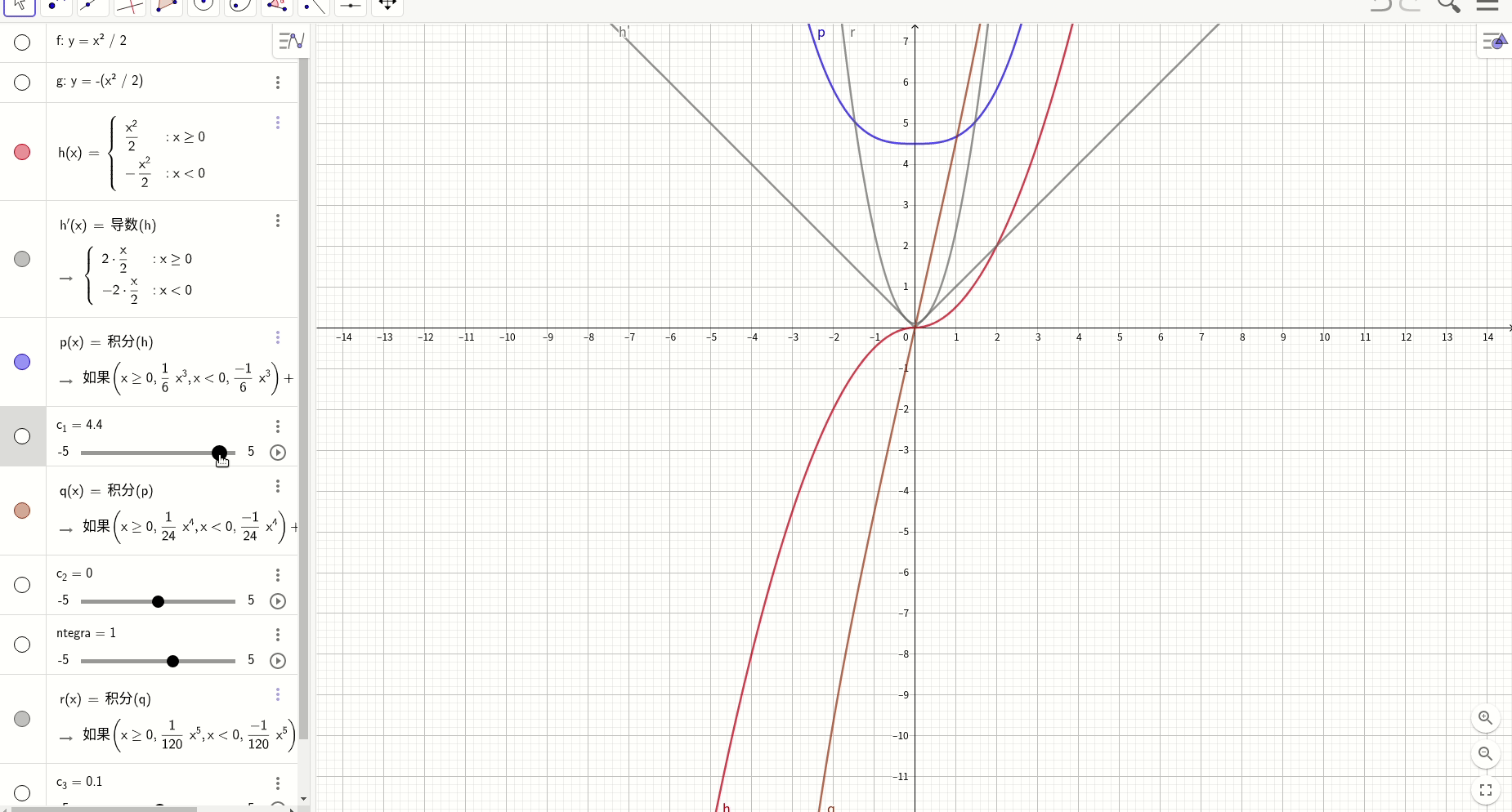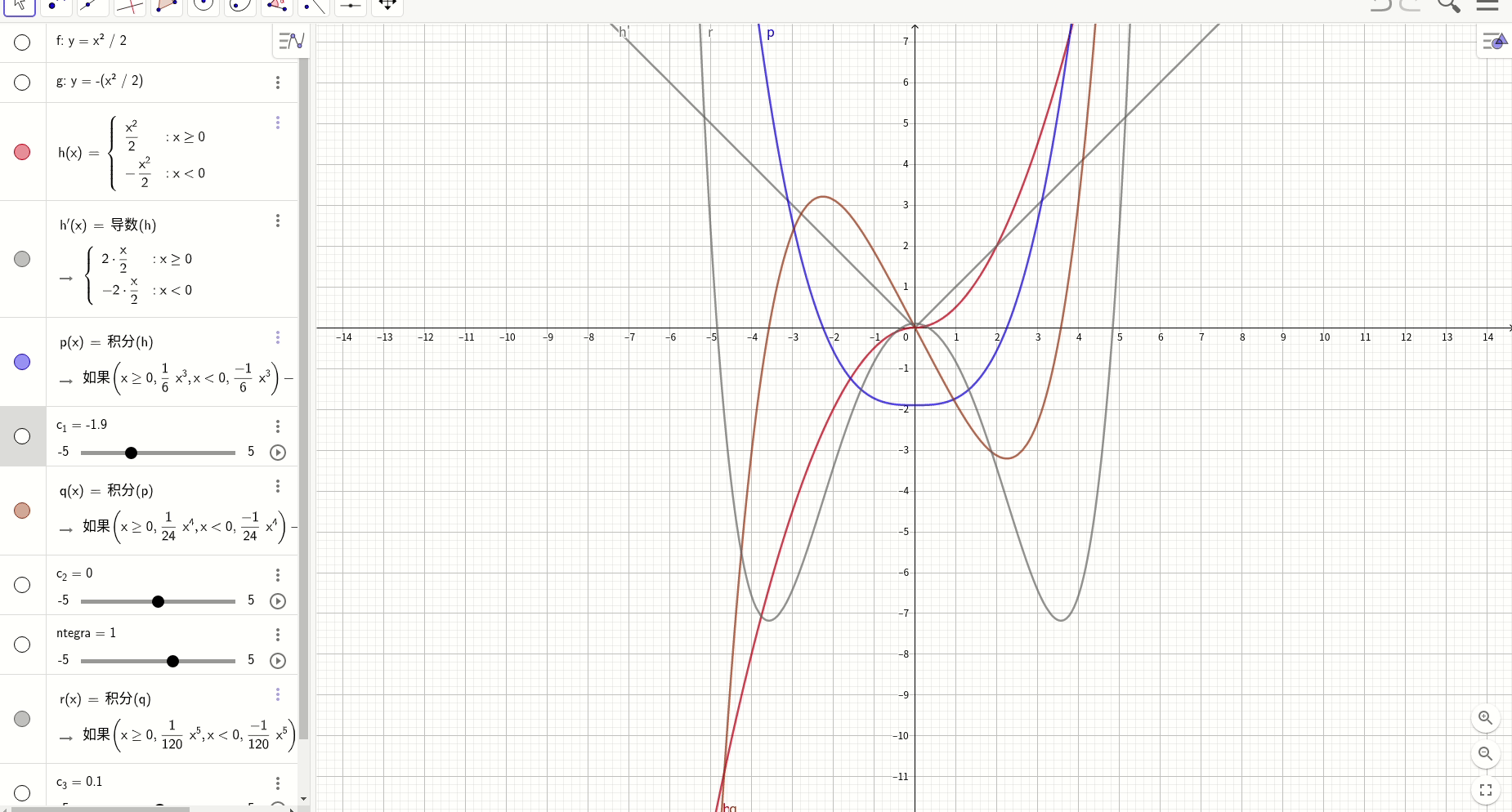
因果律，特解是通解的包络线

对于特解： $y=ax^2$

通解: $y=ax^2+bx$

其极点轨迹: $(-\frac{b}{2a},\frac{-b^2}{4a})$ ，极点轨迹解析式为： $y=-ax^2$

人的感觉

在人的直觉里面，对于那种连续并且无穷持续可微的函数是比较喜欢的，例如y=e^x，因为它无穷光滑。但是我们对那种看似光滑实际上却并非如此的曲线并没有太多直觉。可能这个特点和人的视觉机制有关系，就像观察远处的树林，你并不能看清一颗一颗的树，而仅仅是看到一个轮廓。下面的一个例子说明了一个看似光滑的函数，在经历有穷此求导后，变成了一个带有尖峰的不可微函数

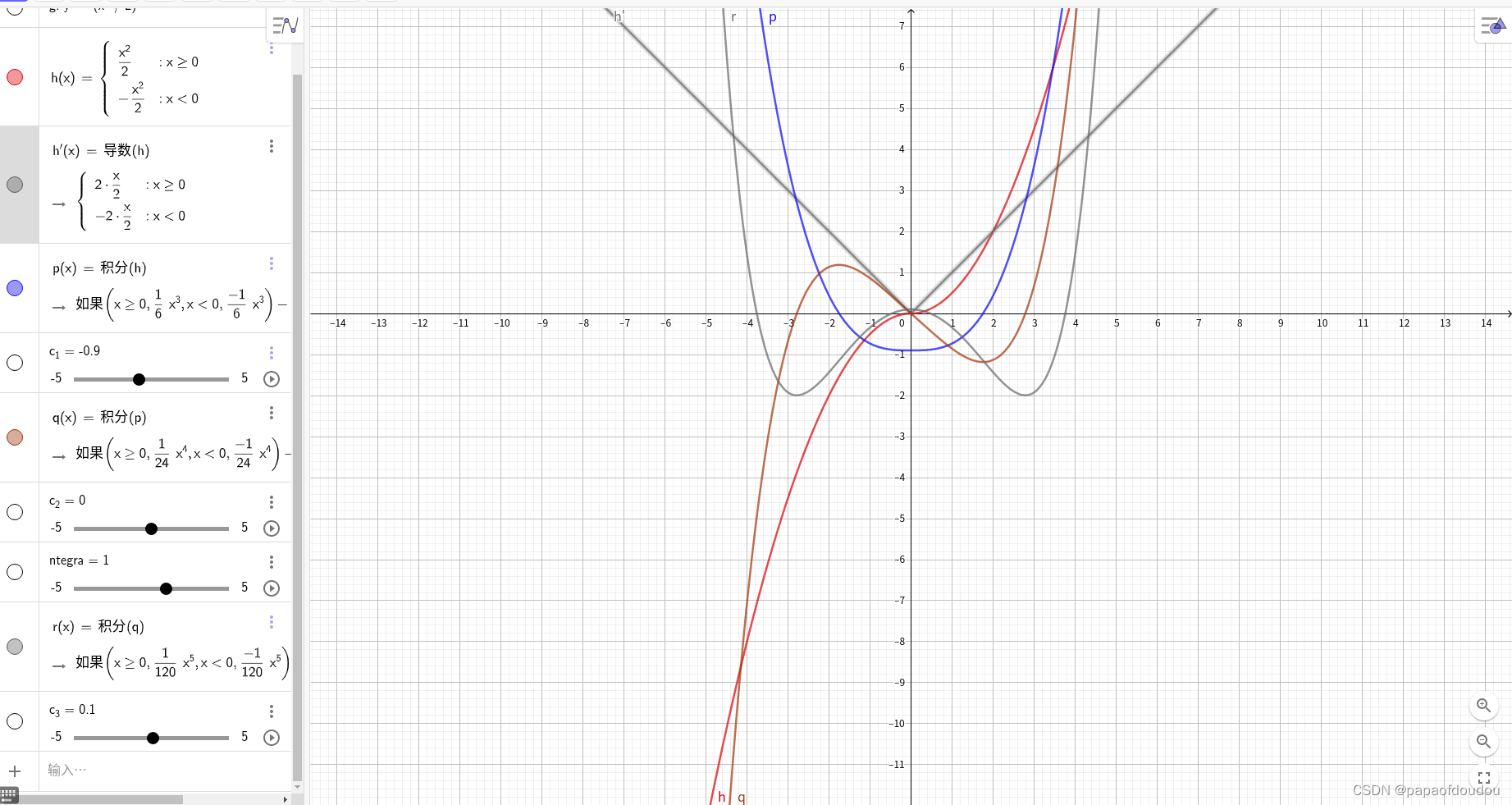
维尔斯特拉斯级数曲线：

下面是一个非常著名的函数魏尔斯特拉斯函数的图形，魏尔斯特拉斯函数的特征是处处连续，但却处处不可导，翻译成人话就是你无法用笔画出它其中的哪怕任何片段，因为人的手臂是有质量的，有质量的物体动起来是有惯性，惯性携带了趋势信息，而这个函数图像不带有任何趋势信息，也就是你看不出任何微观上的走势，就是这么任性，现实中或许只有股票走势曲线能和它媲美了，是不是很神奇？如果牛顿和莱布尼兹两位神仙知道有这类函数的存在，不知道还能不能发明微积分 :). 不过，在数学创造中，自由创造会领先于形式化和逻辑基础．这类函数还有很多，因为不能用初等函数的解析式来表达，被称为病态函数，实际上，就像宇宙中的暗物质远远多于普通物质一样，病态函数的数量要远远多于基本初等函数的变换形式，或者这个世界的本质是病态的．

维尔斯特拉斯函数的解析表达是：

$\sum_{n=0}^{\infty }(\frac{1}{2})^ncos(5^n\pi x)$

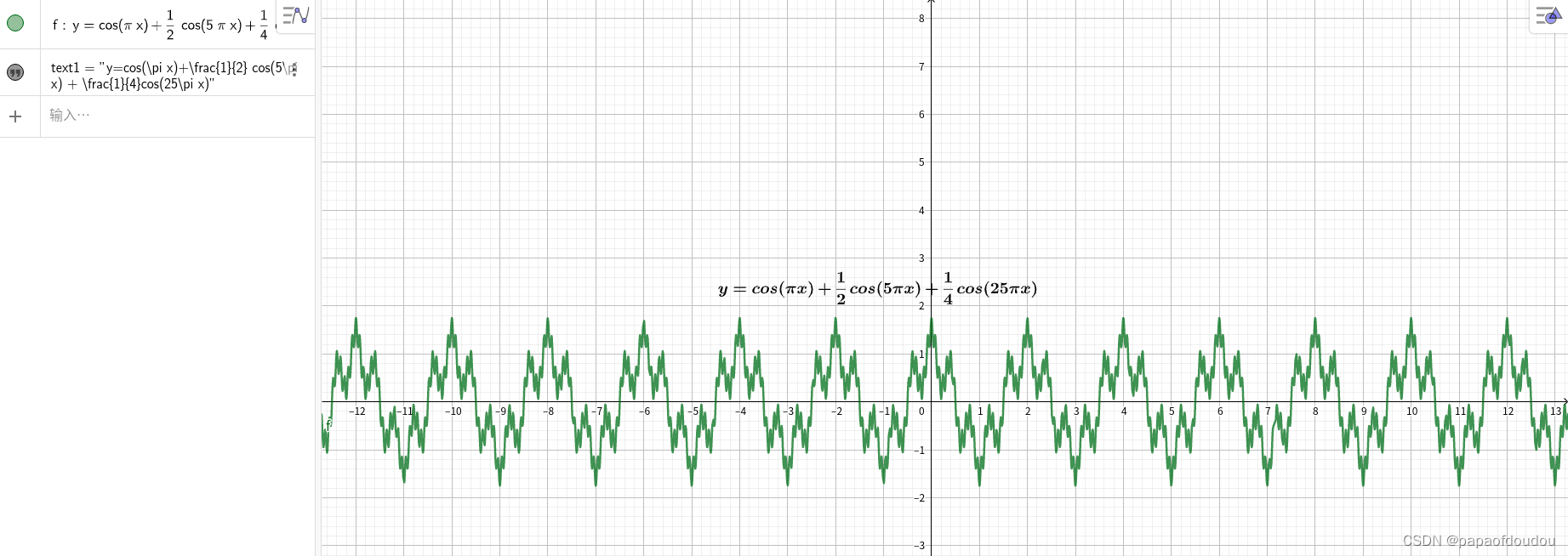
更高阶的维尔斯特拉斯函数

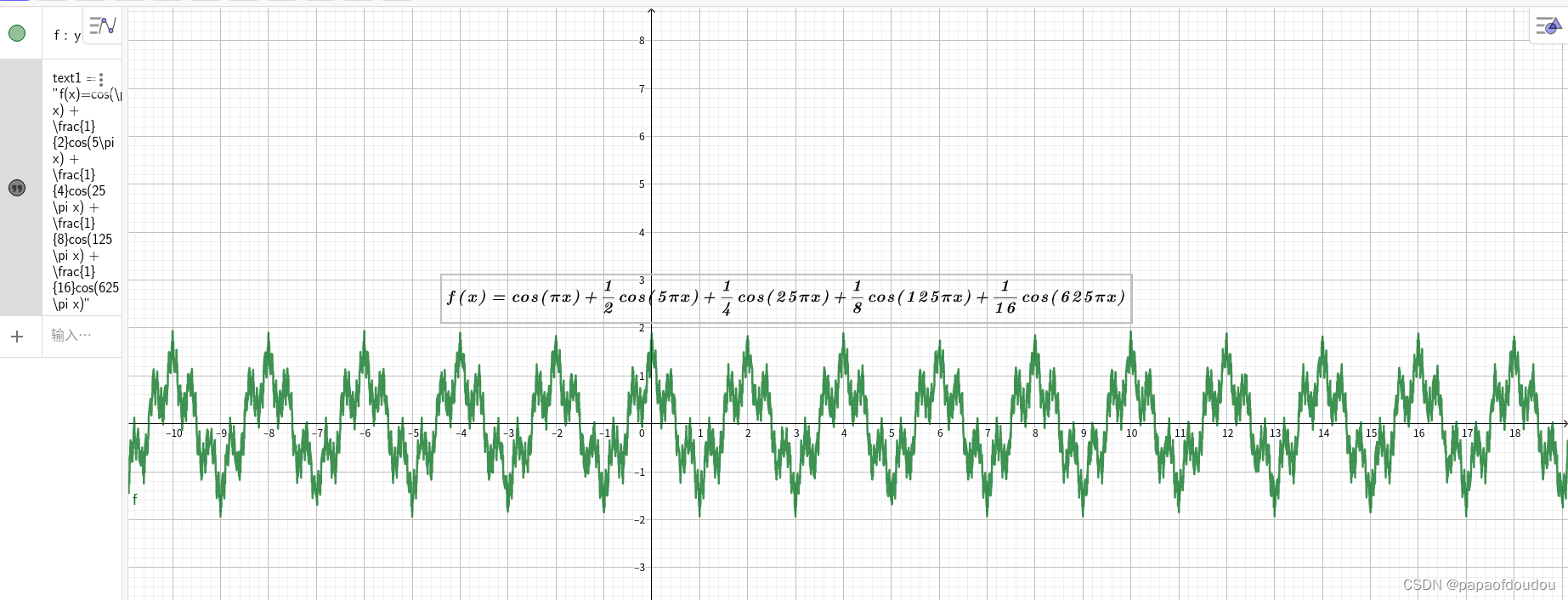
100序列的维尔斯特拉斯函数图形:

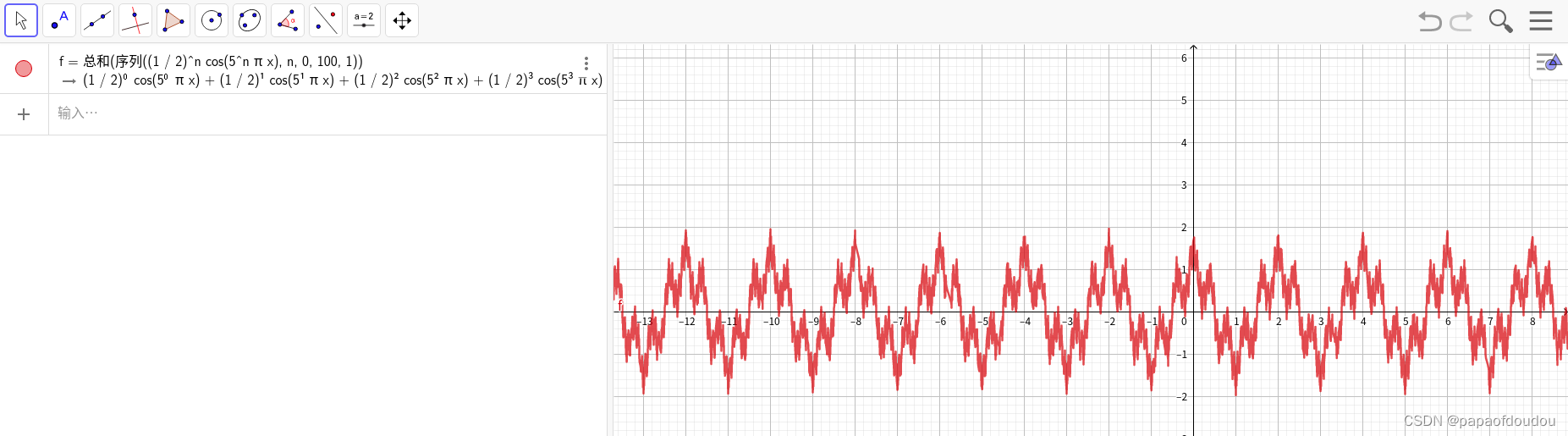
立方和级数

网上看到一个讲解立方级数和的段子，采用数形结合的方式，非常有启发性，这里简单记录下思路：

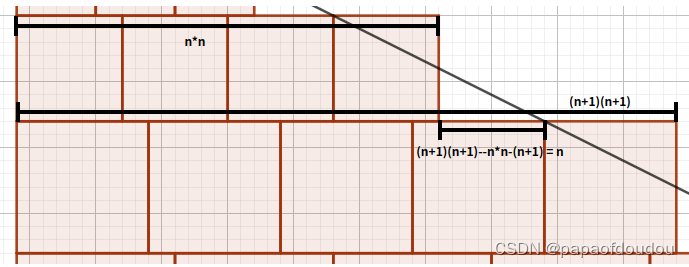
$\large \sum_{i=1}^{n} i^3 = 1\times 1^2 + 2\times 2^2+3\times 3^2+4\times 4^2 + \cdots + n \times n^2$

图形化计算级数和的一种方式：

斜率为1/2，所以大三角形中白色的空缺部分恰好可以由它左上角的多余出去的部分的面积填充过去，构成一个完整的三角形，所以级数合转化为求大三角形的面积：

$\large \boldsymbol{\sum_{i=1}^{n} i^3 = 1\times 1^2 + 2\times 2^2+3\times 3^2+4\times 4^2 + \cdots + n \times n^2=\frac{1}{2}\cdot \frac{n(n+1)}{2}\cdot n(n+1)=\bigg[\frac{n(n+1)}{2}\bigg]^2}$