∫
x
f
′
(
x
)
d
x
\int xf{'}(x)\,{\rm d}x
∫xf′(x)dx
=
∫
x
d
f
(
x
)
=\int x\,{\rm d}{f(x)}
=∫xdf(x)
=
x
f
(
x
)
−
∫
f
(
x
)
d
x
=xf(x)-\int f(x)\,{\rm d}x
=xf(x)−∫f(x)dx
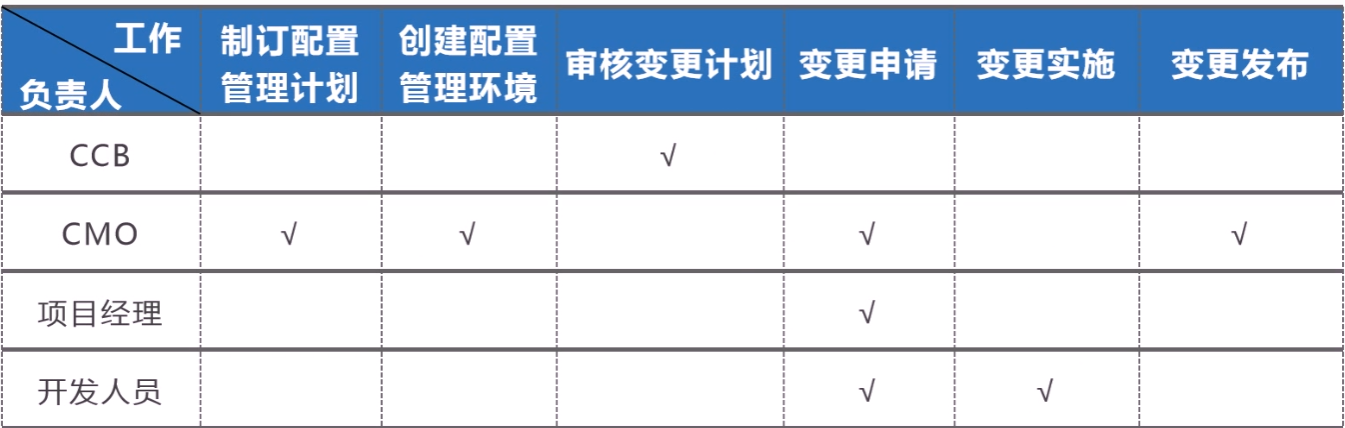
由题知:
f
(
x
)
=
(
ln
2
x
)
′
=
2
ln
x
×
1
x
=
2
ln
x
x
f(x)=({\ln}{^2} x){'}=2\ln x\times\frac{1}{x}=\frac{2\ln x}{x}
f(x)=(ln2x)′=2lnx×x1=x2lnx
原式
=
2
ln
x
−
ln
2
x
+
C
=2\ln x-\ln^2 x+C
=2lnx−ln2x+C




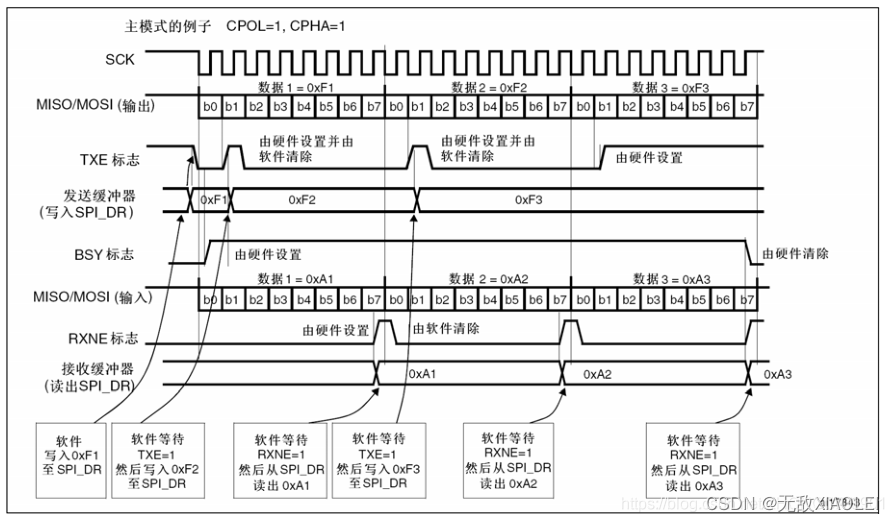

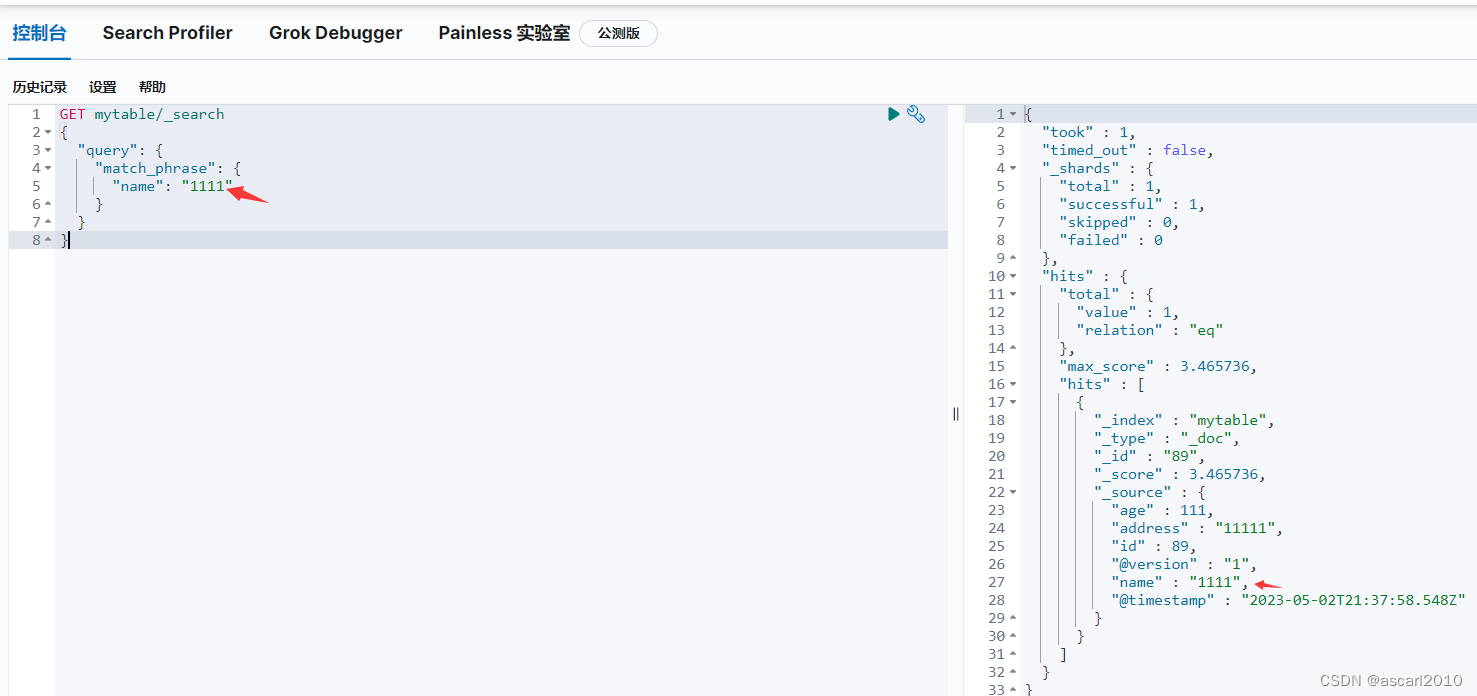


![[架构之路-179]-《软考-系统分析师》-19- 系统可靠性分析与设计 -1- 故障模型、可靠性模型、可靠性分析](https://img-blog.csdnimg.cn/f38135dbfcce4e41b4ed8df5eb33851f.png)


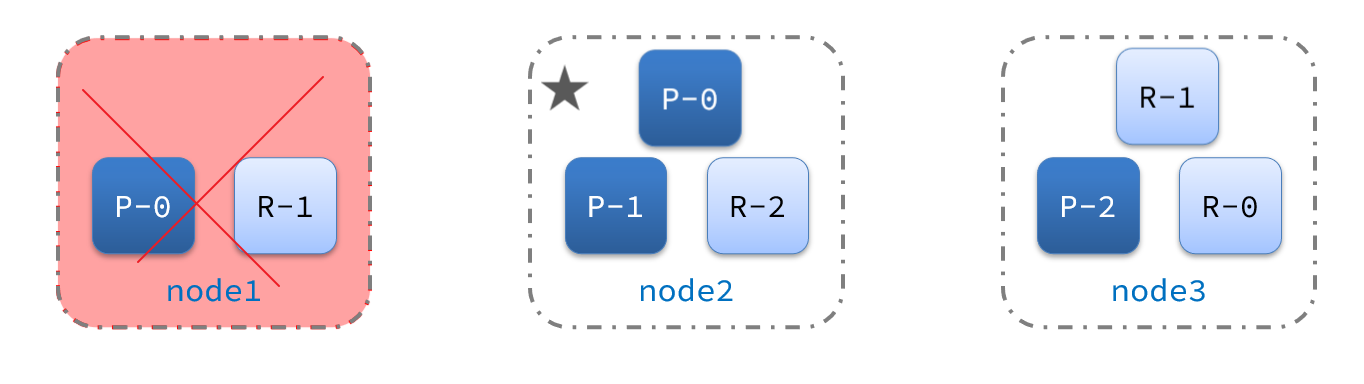

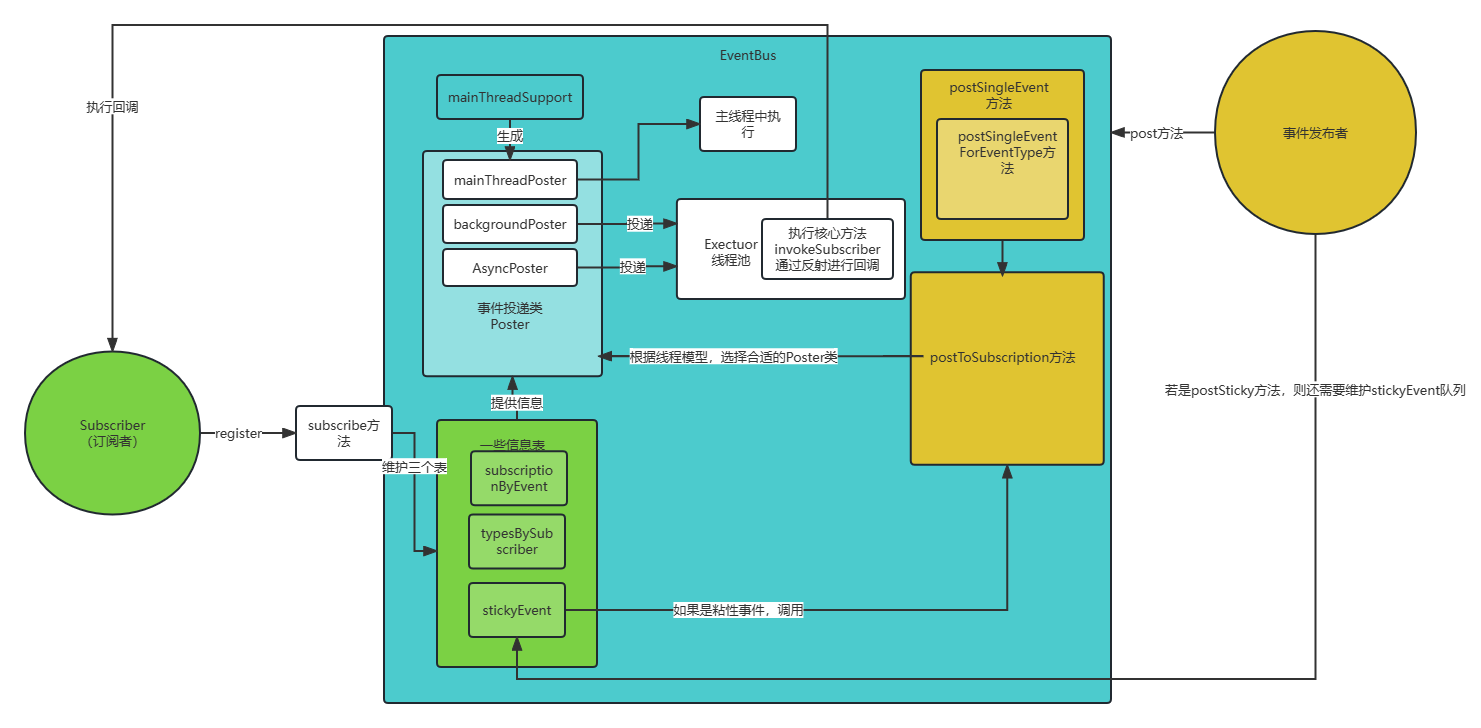
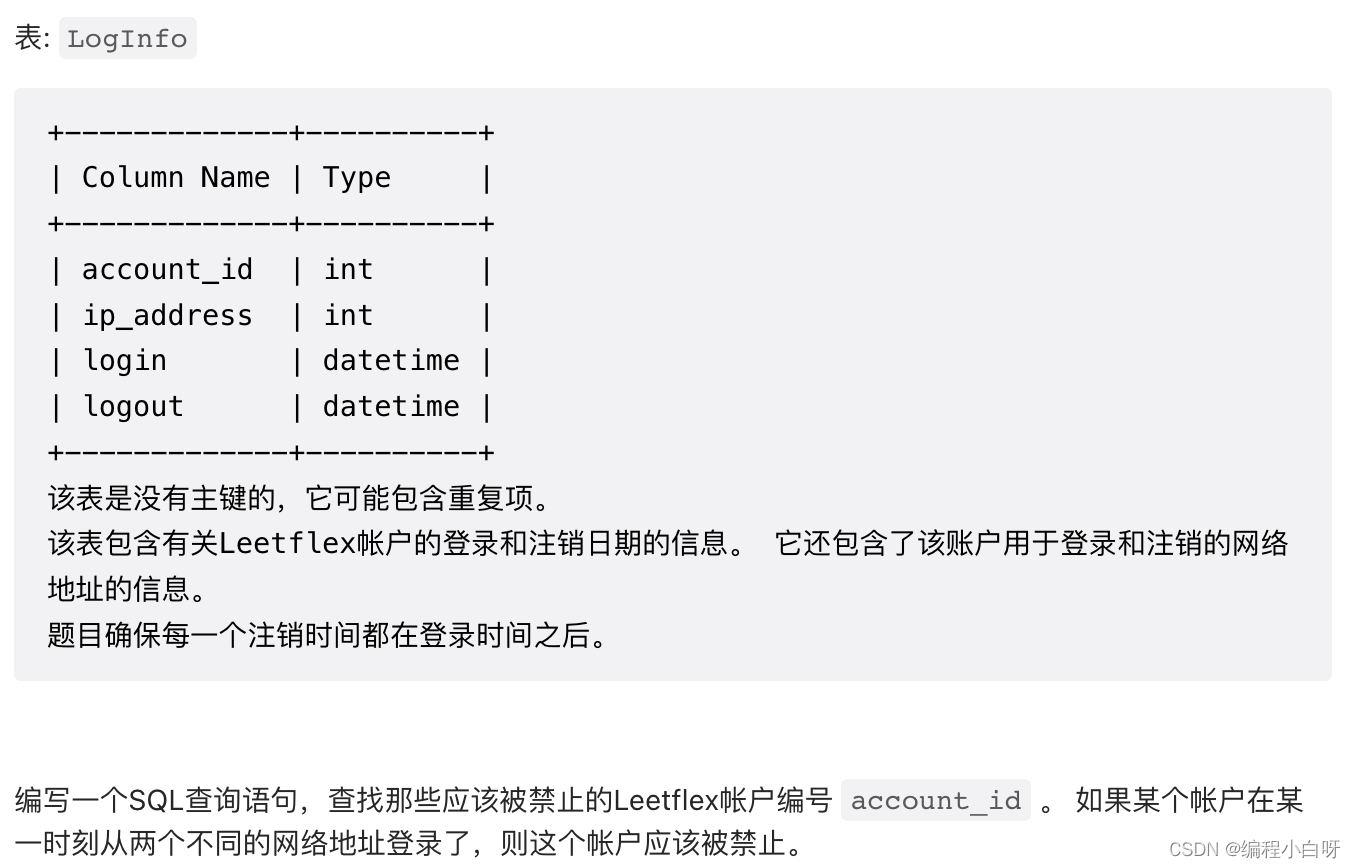
![[架构之路-178]-《软考-系统分析师》-17-嵌入式系统分析与设计- 3- 分区操作系统(Partition Operating System)概述](https://img-blog.csdnimg.cn/img_convert/f6127803753a2c50d6fbf3c886530e08.png)
![[计算机图形学]光场,颜色与感知(前瞻预习/复习回顾)](https://img-blog.csdnimg.cn/fe9d60e5fd0b4bf18f86d88e272243d1.png)