【车间调度】基于模拟退火优化算法的的并行车间机器优化调度（Matlab代码实现）

news2024/11/26 1:33:33

1 概述

2并行机调度问题的的描述

3 模拟退火法

4 基于模拟退火优化算法的的并行车间机器优化调度（Matlab代码实现）

4.1 运行结果

5 参考文献

6 Matlab代码

1 概述

并行机调度（也称并行多机调度, Parallel MachinesScheduling Problem,简称PMSP问题)是实际生产过程中的一类典型调度问题,其研究n个工件J，…,J.}在m台机器{M,,…，Mm}]上的加工过程,每个工件只有一道工序"。在并行机调度问题中，当每台机器均能满足各工件的加工时,此时的调度解主要考虑所有工件在各机器上的划分问题,或者说,如何将m台机器分配给n个工件。以最大完工时间最小为优化日标的并行机调度问题已经被证明是NP完全问题。

2并行机调度问题的的描述

对于n个工件m台机器的并行机调度问题，如果不考虑同-一台机器上加工各工件之间的准备时间,用t,表示工件i的加工时间,W，表示加工过程中该工件等待加工的时间,C表示该工件的加工完毕时间,用f表示所有工件的最大完工时间,则有：

3 模拟退火法

智能优化算法——模拟退火法（Python&Matla实现）

4 基于模拟退火优化算法的的并行车间机器优化调度（Matlab代码实现）

4.1 运行结果

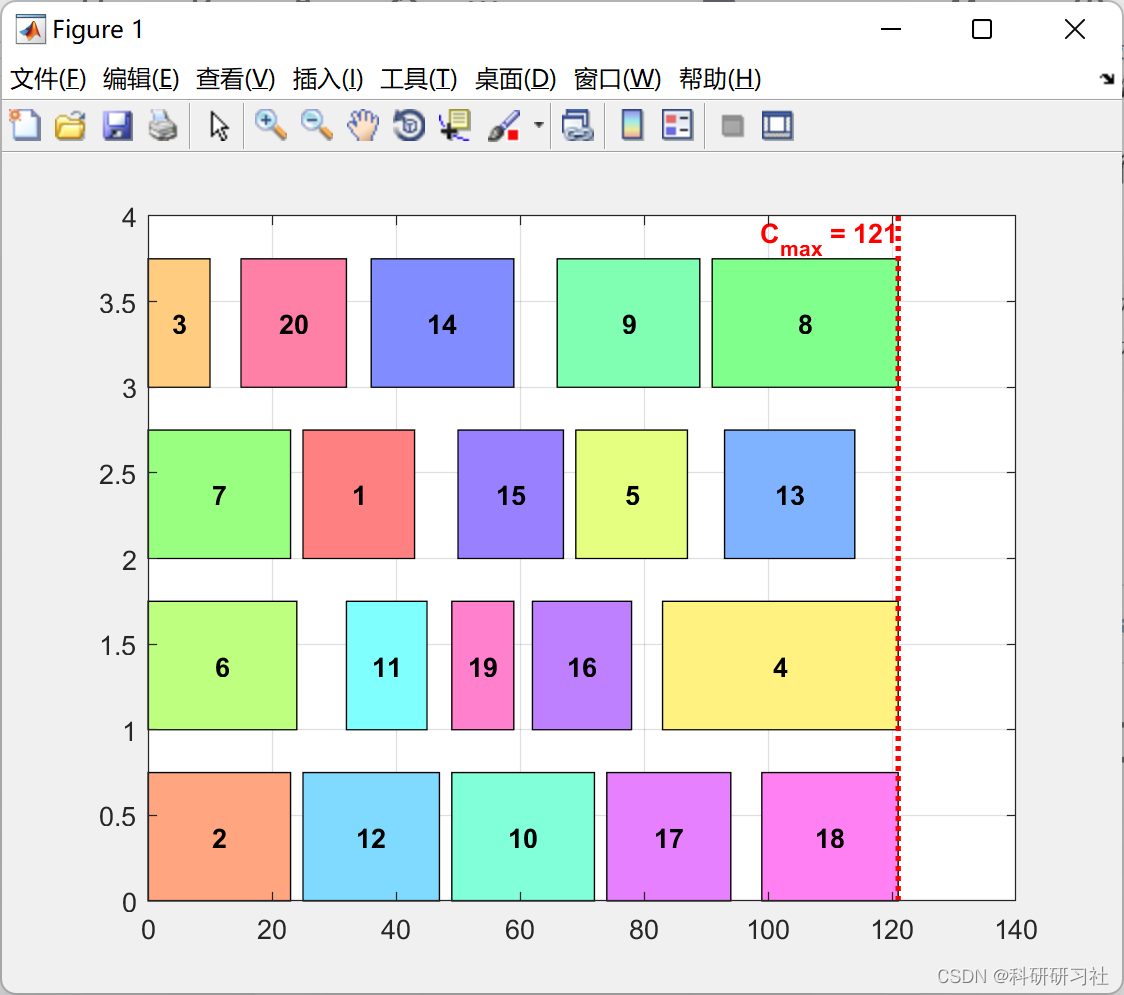
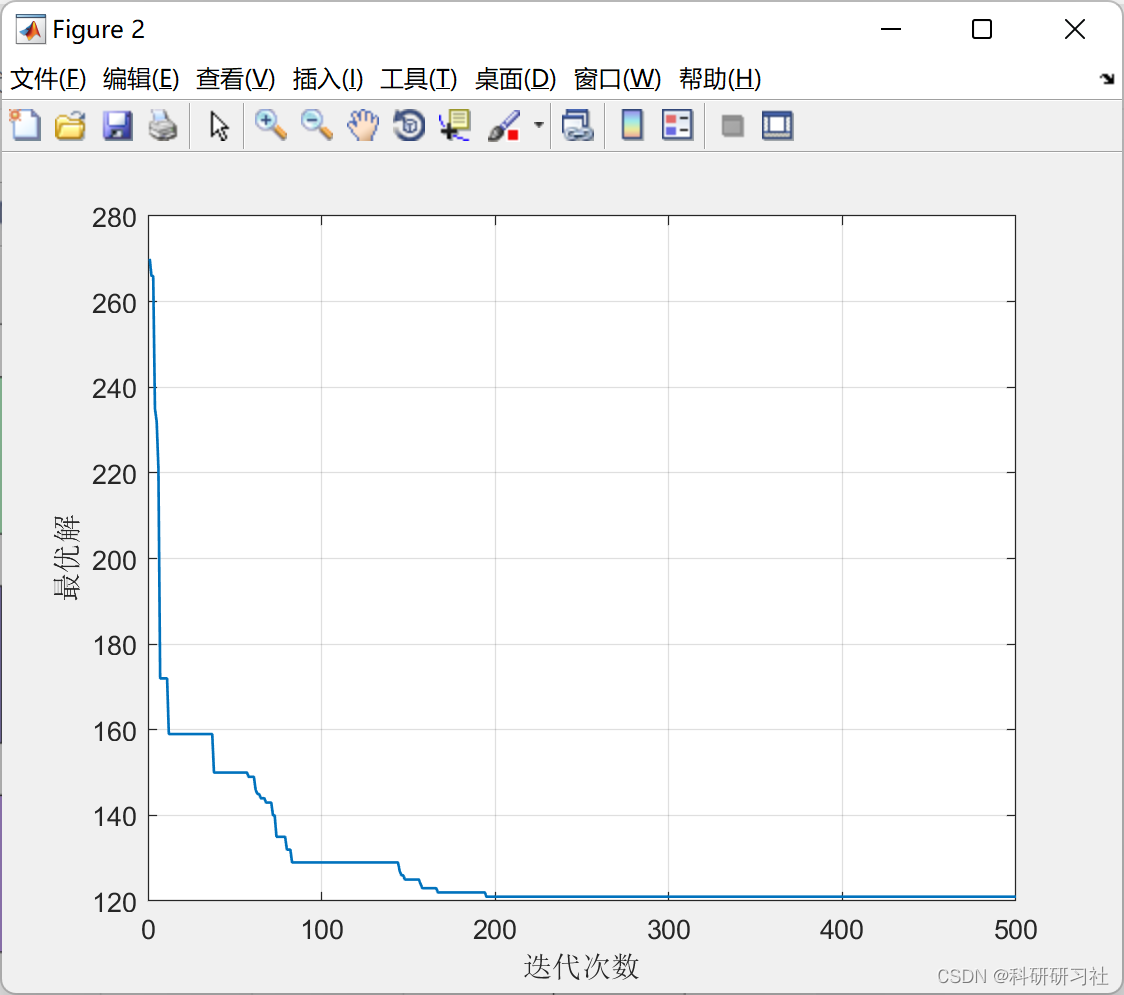
部分代码



function sol=ParseSolution(q,model)

    I=model.I;
    J=model.J;
    p=model.p;
    s=model.s;
    
    % Delimiters Position
    DelPos=find(q>I);
    
    % Determine Start and End of Machines Job Sequence
    From=[0 DelPos]+1;
    To=[DelPos I+J]-1;
    
    % Create Jobs List
    L=cell(J,1);
    for j=1:J
        L{j}=q(From(j):To(j));
    end
    
    % Time-based Simulation
    ST=zeros(I,1);
    PT=zeros(I,1);
    FT=zeros(I,1);
    MCT=zeros(J,1);
    for j=1:J
        for i=L{j}
            k=find(L{j}==i);
            if k==1
                ST(i)=0;
            else
                PreviousJob=L{j}(k-1);
                ST(i)=FT(PreviousJob)+s(PreviousJob,i,j);
            end
            
            PT(i)=p(i,j);
            
            FT(i)=ST(i)+PT(i);
        end
        
        if ~isempty(L{j})
            MCT(j)=FT(L{j}(end));
        end
        
    end
    
    Cmax=max(MCT);
    
    sol.L=L;
    sol.ST=ST;
    sol.PT=PT;
    sol.FT=FT;
    sol.MCT=MCT;
    sol.Cmax=Cmax;

end

针对并行机调度问题的粒子群算法进行了设计，首先提出了基于机器和 PPR的粒子编码方法以及基于工件和PPS 的粒子编码方法。针对在基于机器和 PPR的粒子编码方法中容易产生不可行调度方案的缺点,对其粒子群算法进行了改进,改进后的算法在优化结果上有较好的提高。在此基础上,本文给出了基于两种不同粒子编码方法的粒子群算法步骤。
其次,将基于上述两种不同粒子表示方法的粒子群算法,对7工件3机器并行机调度问题和30工件10机器并行机调度问题两种不同规模的算例进行了测试,实验结果显示,基于两种不同粒子编码方法的粒子群算法均能够得到较好的优化结果,其中基于基于工件和 PPS粒子编码的粒子群算法的优化性能较好，对于30工件I0机器的并行机调度问题,其计算结果好于遗传算法的计算结果。