文章目录
- Part.I 预备知识
- Chap.I 一些前提和概念
- Chap.II lowbit 函数
- Part.II 树状数组
- Chap.I 树状数组的思想
- Chap.II 树状数组的构造
- Part.III 树状数组的应用
- Chap.I LeetCode: 2426. 满足不等式的数对数目
- Sec.I 题目描述与分析
- Sec.II 代码实现
- Chap.II LeetCode: 51. 数组中的逆序对
Part.I 预备知识
参考:
树状数组简单易懂的详解
Chap.I 一些前提和概念
- 负数在计算机中的二进制表示
- 前缀和:前缀和指一个数组的某下标之前的所有数组元素的和(包含其自身)。前缀和分为一维前缀和,以及二维前缀和。前缀和是一种重要的预处理,能够降低算法的时间复杂度。比如,一维前缀和的公式:
sum[i] = sum[i-1] + arr[i] ;sum是前缀和数组,arr是内容数组。拥有前缀和数组后,我们可以在O(1)的时间复杂度内求出区间和。 - 后缀和:
- 离散化:把无限空间中有限的个体映射到有限的空间中去,以此提高算法的时空效率。通俗的说,离散化是在不改变数据相对大小的条件下,对数据进行相应的缩小。当数据只与它们之间的相对大小有关,而与具体是多少无关时,可以进行离散化。设有四个数
1234567, 123456789, 12345678, 123456,我们先对它们进行排序123456<1234567<12345678<123456789 → 1<2<3<4;所以原数据就可以映射为:2, 4, 3, 1。
Chap.II lowbit 函数
暂且不考虑它的用途,首先了解这个函数是怎么算的。顾名思义,lowbit这个函数的功能就是求某一个数的二进制表示中最低的一位1,举个例子,x = 6,它的二进制为110,那么lowbit(x)就返回2,因为最后一位1表示2。
怎么求lowbit呢?一般有两种方式:
- 先消掉最后一位
1(x & (x - 1),x-1并不会影响lowbit左边的1),然后原数减去消掉最后一位1后的数x - (x & (x - 1))。比如8位机中x = 24的二进制表示为00001100,x - 1的二进制表示为00001011,x & (x - 1)的二进制表示为00001000,所以x - (x & (x - 1))其二进制表示为00000100就是我们要的lowbit。 - 根据『计算机表示负数的方法』(2的补码),数本身与数取反的与(
x & -x)。比如8位机中x = 24的二进制表示为00001100,-x的二进制表示为11110100,x & -x的二进制表示为00000100就是我们要的lowbit。
Part.II 树状数组
树状数组是一种数据结构,为什么要构造这样的数据结构呢?这是因为它在解决某些问题方面有其独特的优势。考虑这样一个问题:现有一个长度为n的数组a[n],我们想对其进行一些操作:比如『查询』(查询某个区间的所有元素的和),『更新』(将某个元素的值更改一下)。现在我想做q次更新和q次查询,这q次更新和q次查询是穿插操作的!
如果采用原始的数据结构,每一次『更新』的时间复杂度为O(1)(因为我想改i的值的话直接a[i]=value即可),每一次『查询』的时间复杂度为O(n)(因为要求n个数的和,就要做一个长度为n的循环);
如果采用树状数组的话,每一次『查询』的时间复杂度就可以减小到O(log(n)),但是每一次『更新』的时间复杂度也是O(log(n))。为什么呢?原因暂且不表,后面会详细分析。
Chap.I 树状数组的思想
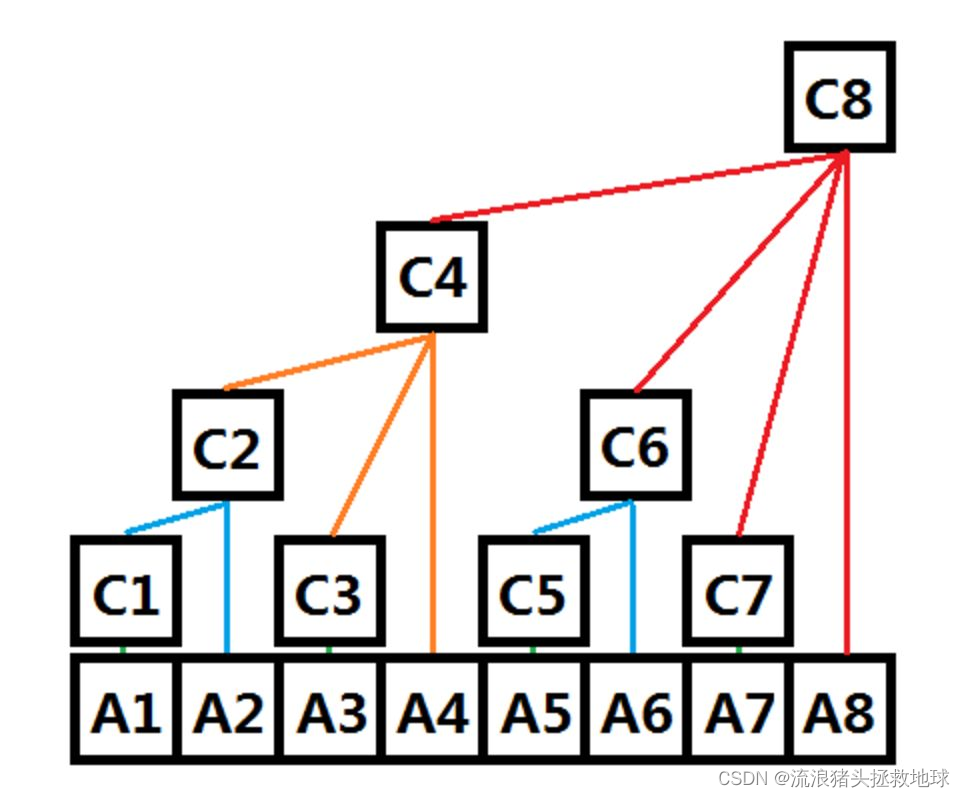
下面先上一个图(来源于 知乎@orangebird)
不行的话,再上一个(来源于 CSDN@FlushHip)
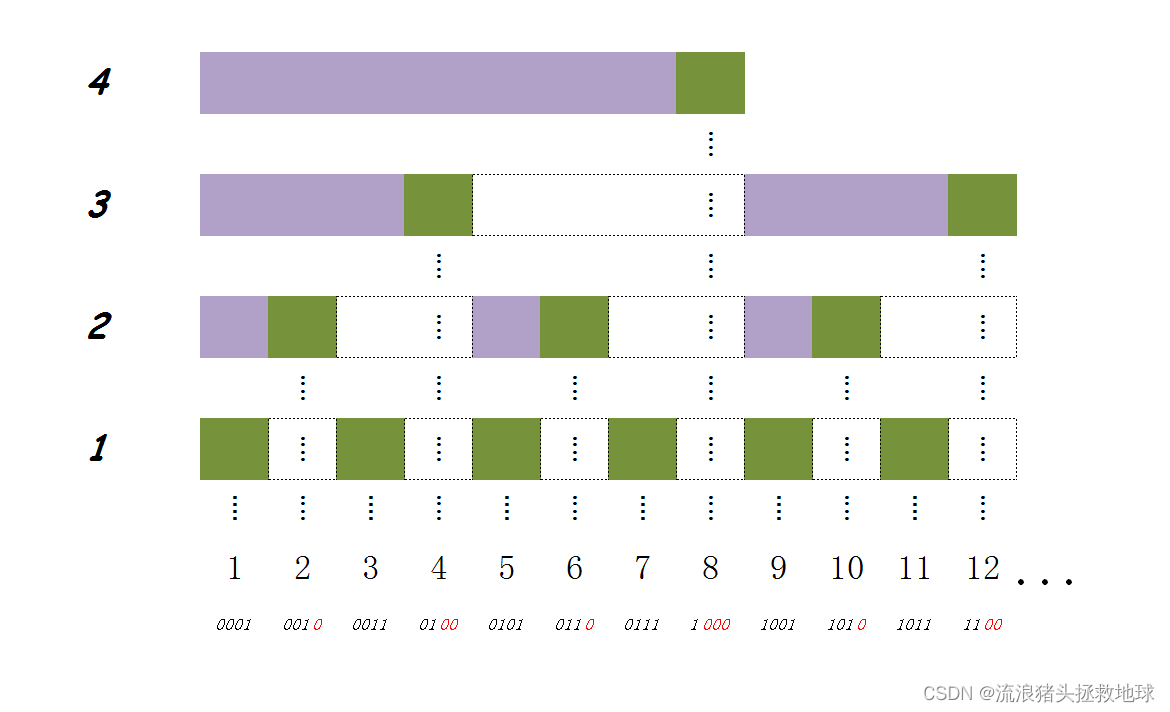
树状数组结构(因为它的结构像数,又是数组所以叫做树状数组)是依托于二进制的,看着上面的图可以很清晰地掌握它的思路,但是为甚么要这样划分呢?这就要用到上面的lowbit了,下面考虑一个长度为8的数组a,新数组叫做c,新数组由旧数组通过上图的组织方式得到。
- 查询:比如我想求
sum(1:7),首先7的二进制表示为111, ∑ i = 1 n = 7 a i = ( a 1 + a 2 + a 3 + a 4 ) + ( a 5 + a 6 ) + a 7 \sum\limits_{i=1}^{n=7}{a_i}=(a_1+a_2+a_3+a_4)+(a_5+a_6)+a_7 i=1∑n=7ai=(a1+a2+a3+a4)+(a5+a6)+a7,写成伪码的方式(数组下标是二进制)就是sum(001:111)=c[111]+c[110]+c[100],就是sum(1:7)=c[7]+c[7-lowbit(7)]+c[6-lowbit(6)],时间复杂度就是 ⌈ l o g 2 ( n ) ⌉ \lceil log_2(n) \rceil ⌈log2(n)⌉,即O(log n)。 - 更新:比如我想更改
a[3]的值,首先3的二进制表示为0011,那么对于长度为8的数组,我需要更新c[3], c[4], c[8];换言之,我就需要更新(二进制下标)a[0011], a[0100], a[1000];也就是说,我需要更新a[3], a[3+lowbit(3)], a[4+lowbit(4)]。显然,它的时间复杂度也是O(log n)。
上面就解释了树状数组的『查询』和『更新』操作为什么时间复杂度是
O(log n)的原因。
之前的我有个疑问:那为什么不同时保存a和c呢?如果要做更新操作,直接在a上做,时间复杂度为O(1);如果要做查询操作,在c上做,时间复杂度是O(log n)。注意,『查询』和『更新』操作是交替进行的,在a上做『更新』,只有重构c之后,做后续『查询』时才能体现出『新息』,但是重构c的时间复杂度就是O(n),这样搞的话,优化就优化了个寂寞。
Chap.II 树状数组的构造
根据上面的讨论,构造出这样一个类,其中包含的函数有:
lowbit:获取一个整数的lowbitBIT:构造函数,根据vector<int>初始化update:更新函数,第i>0个数加valquery:查询函数,返回前m个数的和print:输出tree
class BIT {
private:
int n; // the length of the tree
vector<int> tree; // the data tree
public:
int lowbit(int x) { return x & -x; }
BIT(vector<int> a)
{
n=a.size();
vector<int> temp(n,0);
tree=temp;
for(int i=0;i<n;i++)
{
update(i+1,a[i]);
}
}
/**
* @brief updata the tree array
* @param[in] i the index, >=1
* @param[in] val the value of the update, =now-origin
* @return none
*/
void update(int i, int val)
{
for(;i<=n;tree[i-1]+=val,i+=lowbit(i));
}
/**
* @brief query the summary of the first m terms
* @param[in] m the index, >=1
* @param[out] sum the sum
* @return int
*/
int query(int m)
{
int sum=0;
for(;m>0;sum+=tree[m-1],m-=lowbit(m));
return sum;
}
void print()
{
for (int i = 0; i < n; cout << tree[i] << " ", i++);
cout << endl;
}
};
调用示例:
int main()
{
int test[7]={1,2,3,4,5,6,7};
vector<int> origin(test, test + 7);
BIT bt(origin);
bt.print(); // 打印 tree 的内容
cout<<bt.query(5)<<endl; // 输出前5项和
bt.update(3,6); // 第3项加6
bt.print(); // 打印更新后的 tree 的内容
cout<<bt.query(5)<<endl; // 输出更新后的前5项和
getchar();
return 0;
}
// ----------------- output ------------------
1 3 3 10 5 11 7
15
1 3 9 16 5 11 7
21
上面的代码可以免费下载:下载地址
Part.III 树状数组的应用
- LeetCode: 2426. 满足不等式的数对数目
- 剑指 Offer 51. 数组中的逆序对
Chap.I LeetCode: 2426. 满足不等式的数对数目
没错,就是因为刷题的时候遇到这个题
2426,所以才有这篇笔记的,最后终于露出了獠牙(RUA!!)。
Sec.I 题目描述与分析
首先,题目描述为:
给你两个下标从 0 开始的整数数组 nums1 和 nums2 ,两个数组的大小都为 n ,同时给你一个整数 diff,统计满足以下条件的数对 (i, j) :
0 <= i < j <= n - 1- 且
nums1[i] - nums1[j] <= nums2[i] - nums2[j] + diff
请你返回满足条件的 数对数目 。
解题视频:bilibili@灵茶山艾府
题目分析(基于python):
- 首先进行移项:
nums1[i] - nums2[i] <= nums1[j] - nums2[j] + diff,令nums[i] = nums1[i] - nums2[i],我们只需找到当0 <= i < j <= n - 1时满足nums[i] <= nums[j] + diff的所有数据对(i, j)即可。 - 因为
nums[i]中不免会存在数值相同的元素,因此我们可以将其用set进行唯一化,然后进行排序得到b。 - 离散化:构造一个树状数组
bt(所有元素初始化为0),树状数组的长度等于num中互异元素的个数len(set(nums))(相当于将nums分为这么多档次【不论数据大小,只关心数据的相对大小,这就是离散化】,树状数组的每一个元素存储的是在这个档次的数据个数)。树状数组有两个主要函数,一个是add(x)(将索引为x的值加一,这里值的是上面的A,但是树状数组存储的是C,所以要变的不只一个元素),另一个是query(x)(求索引小于x的所有数据的和)。 - 我们用一个指针
i遍历nums,在遍历的过程中并填充树状数组bt,树状数组存储的是x=nums[i]左边每一个『档次』元素的个数,我们先用index=bisect_right(b, x + diff)在b中找到元素大于等于x+diff的索引最小值,然后用query(index)统计nums[i]左边元素大于等于x+diff的数目和(也就是找到满足nums[m] <= nums[i] + diff且m<i的所有的m的个数和) - 然后用
index2=bisect_left(b, x)得到b中元素小于等于x的所有元素的索引最大值(也就是找到x所对应的『档次』索引),然后用add(index2)函数将其加入树状数组中去,为进入下一次query(i+1)做准备。 - 对所有的
query(index)求和就得到我们所需
注意,这道题虽然使用了树状数组,但是数组存储的并不是元素值,而是元素个数。另外,树状数组并不是一下就构造好的,而是在遍历查询添加元素的过程中逐步建立的。知道这两点,看着视频讲解应该就很好理解了。笔者已经尝试尽可能地将这个思想整理出来,但是回过头看还是有点拗口 orz
Sec.II 代码实现
下面是C++代码实现
class BIT {
private:
int length=0;
vector<int> tree;
public:
BIT(int n)
{
length=n;
vector<int> temp(n,0);
tree=temp;
}
int lowbit(int x){ return x & -x; }
void add(int i)
{ // i=index+1,>=1
while(i<=length){ tree[i-1]++; i=i+lowbit(i); }
}
int query(int i)
{ // i=index+1,>=1
int sum=0;
while(i>0){
sum+=tree[i-1];
i-=lowbit(i);
}
return sum;
}
};
class Solution {
public:
long long numberOfPairs(vector<int>& nums1, vector<int>& nums2, int diff) {
int n=nums1.size();
vector<int> nums(n,0);
for(int i=0;i<n;i++) { nums[i]=nums1[i]-nums2[i]; }
vector<int> b(nums);
sort(b.begin(),b.end());
b.erase(unique(b.begin(),b.end()),b.end());
BIT bt(b.size());
long ans=0;
for(int i=0;i<n;i++)
{
ans+=bt.query(upper_bound(b.begin(),b.end(),nums[i]+diff)-b.begin());
bt.add(lower_bound(b.begin(),b.end(),nums[i])-b.begin()+1);
}
return ans;
}
};
值得注意的点:
upper_bound(b.begin(),b.end(),val)函数的作用是查找容器b(数据已经有序)中元素值大于等于val的最小索引迭代器(可以理解为指针),*upper_bound(xx)返回索引的元素值,upper_bound(xx)-b.begin()是索引值upper_bound(b.begin(),b.end(),val)函数的作用是查找容器b(数据已经有序)中元素值小于val的最大索引迭代器(可以理解为指针),其他的使用同upper_bound
下面是python的代码实现:
class BIT:
def __init__(self,n: int):
self.length=n
self.tree=[0]*n
def add(self, i: int):
while(i<=self.length):
self.tree[i-1]+=1
i+=(i & -i)
def query(self, i: int) -> int:
sum=0
while(i>0):
sum+=self.tree[i-1]
i-=(i & -i)
return sum
class Solution:
def numberOfPairs(self, nums1: List[int], nums2: List[int], diff: int) -> int:
n=len(nums1)
nums=[0]*n
for i in range(n):
nums[i]=nums1[i]-nums2[i]
b=sorted(set(nums))
bt=BIT(len(b))
ans=0
for i in range(n):
ans+=bt.query(bisect_right(b,nums[i]+diff))
bt.add(bisect_left(b,nums[i])+1)
return ans
Chap.II LeetCode: 51. 数组中的逆序对
这道题应该是比较经典的一道题,毕竟都已经被『剑指 Offer』录入了。它实际上和上面的一道题很像,比那道题简单。因此下面就不分析了,只贴一个解决方案
下面是基于python的代码:
class Solution:
def reversePairs(self, nums: List[int]) -> int:
b = sorted(set(nums))
ans = 0
n = len(b)
bt = BIT(n)
for x in nums:
temp=n-bisect_left(b, x)
ans += bt.query(temp-1)
bt.add(temp)
return ans
class BIT:
def __init__(self,n: int):
self.length=n
self.tree=[0]*n
def add(self, i: int):
while(i<=self.length):
self.tree[i-1]+=1
i+=(i & -i)
def query(self, i: int) -> int:
sum=0
while(i>0):
sum+=self.tree[i-1]
i-=(i & -i)
return sum









![[附源码]计算机毕业设计JAVAjsp闲置物品线上交易系统](https://img-blog.csdnimg.cn/3bb6a04cc9b1433cb514adb16dcd99b1.png)