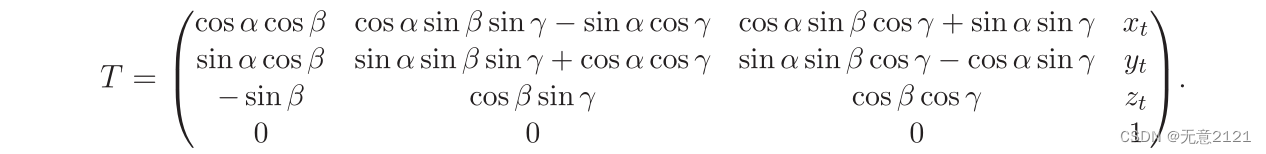目录
1 一般概念
1.1 基元的变换
1.2 一个参数化的变换族
2 2D变换
2.1 translation
2.2 rotation
2.3 Combining translation and rotation
3 3D变换
3.1 Yaw, pitch, and roll rotations
3.2 Determining yaw, pitch, and roll from a rotation matrix
3.3 The homogeneous transformation matrix for 3D bodies
本文对机器人运动规划的经典书籍《planning algorithm》进行解析,原文请参考3.2 Rigid-Body Transformations (lavalle.pl)
1 一般概念
假设刚体机器人a被定义为R2或R3的一个子集。刚体变换是一个函数 h: A→W,它将A的每一点映射到W,有两个要求:1)A的任意两点之间的距离必须保持,2)A的方向必须保持(没有“镜像”)。对于某a∈A, h(a)表示W中被a“占据”的点。
![]()
这是h的像,表示变换后的机器人占据W中的所有点。形象地说就是机器人坐标系转化到世界坐标系的一个映射。
1.1 基元的变换
上述是一整个刚体进行变换,但是对于一个复杂的机器人,我们通常用多个基元的组合来定义,如
![]()
因此变换的函数如下
![]()
如果利用逆映射,则变换的函数如下
![]()
1.2 一个参数化的变换族
将q定义为参数变量,由q来决定A到W的变换。同时将h(q, a)简化为a(q),将h(q, A)简化为A(q)。这可以形象地认为将body frame以一定位置和方向放置到world frame。同时我们也区分一下body frame 和 world frame,在一般机器人的运动规划问题中,world frame基本不会变,一般都是机器人运动,也就是body frame不断地在做刚体变换。
2 2D变换
2.1 translation
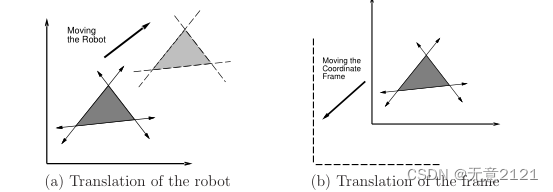
上面介绍的内容还是相对抽象,本节开始就比较具体了,下面就是刚体变换中平移的映射,
![]()
现在考虑用基元定义的A的实心表示形式
![]()
![]()
当然translation有两种形式,第二种相当于机器人“倒退”(根据相对运动)
2.2 rotation
旋转的映射关系如下
![]()
通过2*2的矩阵可以表示为
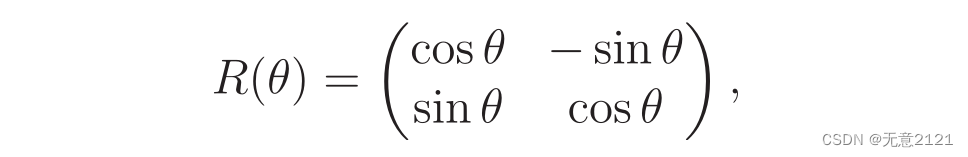

线性代数中提出左乘矩阵相当于对其进行线性变换,这里就是旋转变换,同时回想一下列向量其实表示新坐标系的基向量。R(θ)的列向量是单位向量,它们的内积为零,也表明它们是正交的,理解了这一步,有助于对高维旋转矩阵的理解
2.3 Combining translation and rotation
平移和旋转我们都已经探究了一遍,现在对平移和旋转结合,也就能达到平面的移动机器人真正在做的刚体变换。因为平移和旋转相互独立,所以能直接进行叠加,将旋转矩阵吸收平移的部分,公式如下

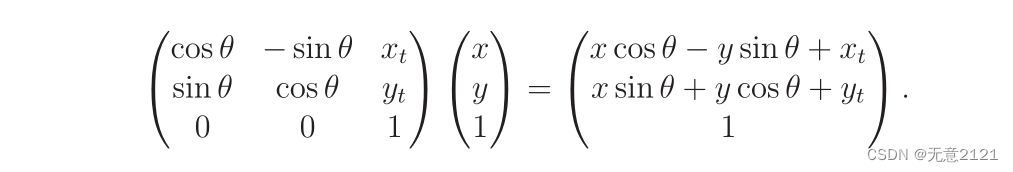
上式左乘的矩阵T被称为齐次变换矩阵。T表示旋转和平移。每个机器人的基元都可以使用T的逆变换,从而得到一个变换后的机器人实体模型。齐次变换矩阵是组合变换的一种简便的表示方法。因此,它经常用于机器人、力学、计算机图形学和其他领域。它被称为齐次变换是因为在R3上它只是一个没有任何平移的线性变换。在射影几何中,增加一维来吸收平移部分的技巧是常见的。
3 3D变换
对于平面移动机器人,如自动驾驶车辆,AGV等,2D变换是非常重要的内容,但对于三维移动机器人,如无人机,机械臂等,3D变换就变得尤为重要。
3.1 Yaw, pitch, and roll rotations
二维刚体变换有两个平移的自由度和一个旋转的自由度,而三维刚体变换有三个平移的自由度和三个旋转的自由度。平移的部分与二维类似,这里就不再赘述。
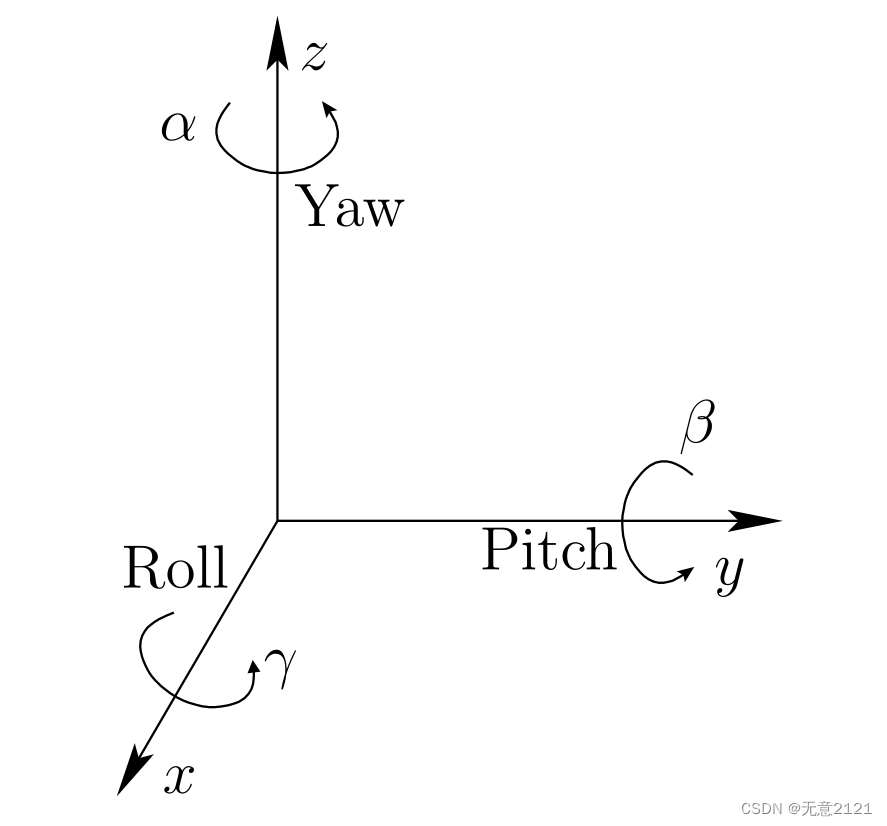
横摆是绕Z轴旋转

俯仰是绕y轴旋转

翻滚是绕x轴旋转
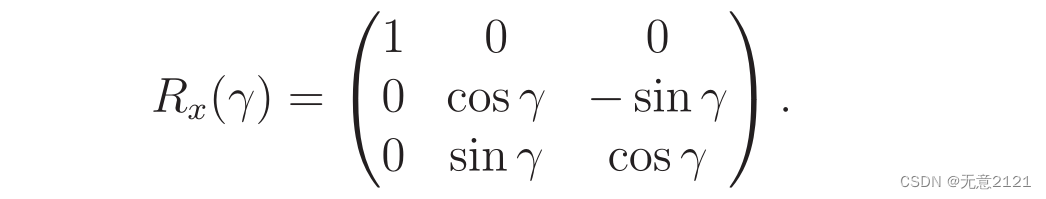
上述三个专业名词根据不同的载体而定,这里主要是六自由度车辆的专业术语。
每个旋转矩阵都是二维旋转矩阵的简单扩展。例如,横摆矩阵Rz(α)本质上执行了一个关于x和y坐标的2D旋转,而保持z坐标不变。三种旋转可将3D体置于任何方向。通过将三个旋转矩阵相乘,可以得到单个旋转矩阵

但要注意左乘矩阵的顺序不同。3D刚体变换的结果不同
3.2 Determining yaw, pitch, and roll from a rotation matrix

直接从给定的旋转矩阵确定α、β和γ参数通常是很方便的。如上式假设一个任意旋转矩阵得
![]()
![]()
![]()
3.3 The homogeneous transformation matrix for 3D bodies
上面对3D刚体的旋转矩阵做了推导,现在来把平移与旋转结合,也就是探究一个3D刚体的齐次变换矩阵,矩阵如下