文章目录

周赛343
- [6341. 保龄球游戏的获胜者](https://leetcode.cn/problems/determine-the-winner-of-a-bowling-game/)
- - 模拟 + 技巧
- [2661. 找出叠涂元素](https://leetcode.cn/problems/first-completely-painted-row-or-column/)
- - 模拟
- [2662. 前往目标的最小代价](https://leetcode.cn/problems/minimum-cost-of-a-path-with-special-roads/)
- - 网格图版求最短路径问题
- [2663. 字典序最小的美丽字符串](https://leetcode.cn/problems/lexicographically-smallest-beautiful-string/)
- - 贪心

周赛343

6341. 保龄球游戏的获胜者

难度简单2

给你两个下标从 0 开始的整数数组 player1 和 player2 ，分别表示玩家 1 和玩家 2 击中的瓶数。

保龄球比赛由 n 轮组成，每轮的瓶数恰好为 10 。

假设玩家在第 i 轮中击中 xi 个瓶子。玩家第 i 轮的价值为：

如果玩家在前两轮中击中了 10 个瓶子，则为 2xi 。
否则，为 xi 。

玩家的得分是其 n 轮价值的总和。

如果玩家 1 的得分高于玩家 2 的得分，则为 1 ；
如果玩家 2 的得分高于玩家 1 的得分，则为 2 ；
如果平局，则为 0 。

示例 1：

输入：player1 = [4,10,7,9], player2 = [6,5,2,3]
输出：1
解释：player1 的得分是 4 + 10 + 2*7 + 2*9 = 46 。
player2 的得分是 6 + 5 + 2 + 3 = 16 。
player1 的得分高于 player2 的得分，所以 play1 在比赛中获胜，答案为 1 。

示例 2：

输入：player1 = [3,5,7,6], player2 = [8,10,10,2]
输出：2
解释：player1 的得分是 3 + 5 + 7 + 6 = 21 。
player2 的得分是 8 + 10 + 2*10 + 2*2 = 42 。
player2 的得分高于 player1 的得分，所以 play2 在比赛中获胜，答案为 2 。

示例 3：

输入：player1 = [2,3], player2 = [4,1]
输出：0
解释：player1 的得分是 2 + 3 = 5 。
player2 的得分是 4 + 1 = 5 。
player1 的得分等于 player2 的得分，所以这一场比赛平局，答案为 0 。

提示：

n == player1.length == player2.length
1 <= n <= 1000
0 <= player1[i], player2[i] <= 10

模拟 + 技巧

题解：翻译有问题

只要发现有一个10后面两个数字进行翻倍就好了。

class Solution:
    def isWinner(self, player1: List[int], player2: List[int]) -> int:
        def calc(sz: List[int]) -> int:
            n = len(sz)
            k = [1] * (n+2) # 统一处理最后两个元素
            for i in range(n):
                if sz[i] == 10:
                    k[i+1] = 2
                    k[i+2] = 2
            # 标记需要翻倍的得分，然后相加
            ans = 0
            for i in range(n):
                ans += sz[i] * k[i]
            return ans
        sum1 = calc(player1)
        sum2 = calc(player2)
        if sum1 == sum2:
            return 0
        elif sum1 > sum2:
            return 1
        else:
            return 2

或者不先预处理，使用dp的思想，遍历i时，查看i-1和i-2位置是否为10

class Solution:
    def isWinner(self, player1: List[int], player2: List[int]) -> int:
        def calc(sz: List[int]) -> int:
            n = len(sz)
            ans = 0
            for i, x in enumerate(sz):
                if i and sz[i-1] == 10 or i > 1 and sz[i-2] == 10:
                    x *= 2
                ans += x
            return ans
        sum1 = calc(player1)
        sum2 = calc(player2)
        if sum1 == sum2:
            return 0
        elif sum1 > sum2:
            return 1
        else:
            return 2

2661. 找出叠涂元素

难度中等5

给你一个下标从 0 开始的整数数组 arr 和一个 m x n 的整数矩阵 mat 。arr 和 mat 都包含范围 [1，m * n] 内的所有整数。

从下标 0 开始遍历 arr 中的每个下标 i ，并将包含整数 arr[i] 的 mat 单元格涂色。

请你找出 arr 中在 mat 的某一行或某一列上都被涂色且下标最小的元素，并返回其下标 i 。

示例 1：

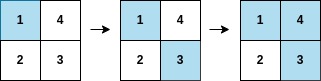
输入：arr = [1,3,4,2], mat = [[1,4],[2,3]]
输出：2
解释：遍历如上图所示，arr[2] 在矩阵中的第一行或第二列上都被涂色。

示例 2：

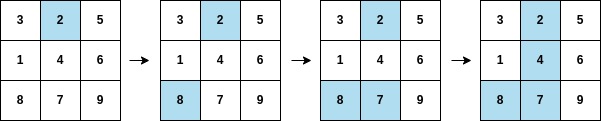
输入：arr = [2,8,7,4,1,3,5,6,9], mat = [[3,2,5],[1,4,6],[8,7,9]]
输出：3
解释：遍历如上图所示，arr[3] 在矩阵中的第二列上都被涂色。

提示：

m == mat.length
n = mat[i].length
arr.length == m * n
1 <= m, n <= 105
1 <= m * n <= 105
1 <= arr[i], mat[r][c] <= m * n
arr 中的所有整数 互不相同
mat 中的所有整数 互不相同

模拟

1wa：注意行列关系，当某行出现次数达到列值时，说明这一行都出现过了

class Solution {
    public int firstCompleteIndex(int[] arr, int[][] mat) {
        Map<Integer, Integer> map = new HashMap<>();
        int m = mat.length, n = mat[0].length;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                map.put(mat[i][j], i * n + j);
            }
        }
        int[] row = new int[m];
        int[] col = new int[n];
        for(int i = 0; i < arr.length; i++){
            int pos = map.get(arr[i]);
            // arr[i] 在原数组的(x, y)位置
            int x = pos / n, y = pos % n;
            row[x]++; // 行和列对应位置 + 1
            col[y]++;
            // 某行或者某列计数满了，说明这一行/列都出现过了
            if(row[x] == n || col[y] == m) return i;
        }
        return -1;
    }
}

python

class Solution:
    def firstCompleteIndex(self, arr: List[int], mat: List[List[int]]) -> int:
        m, n = len(mat), len(mat[0])
        pos = [0] * (m*n + 1)
        for i, row in enumerate(mat):
            for j, x in enumerate(row):
                pos[x] = (i, j)
        row = [0] * m
        col = [0] * n
        for i, x in enumerate(arr):
            x, y = pos[x]
            row[x] += 1
            col[y] += 1
            if row[x] == n or col[y] == m:
                return i
        return -1

2662. 前往目标的最小代价

难度中等10

给你一个数组 start ，其中 start = [startX, startY] 表示你的初始位置位于二维空间上的 (startX, startY) 。另给你一个数组 target ，其中 target = [targetX, targetY] 表示你的目标位置 (targetX, targetY) 。

从位置 (x1, y1) 到空间中任一其他位置 (x2, y2) 的代价是 |x2 - x1| + |y2 - y1| 。

给你一个二维数组 specialRoads ，表示空间中存在的一些特殊路径。其中 specialRoads[i] = [x1i, y1i, x2i, y2i, costi] 表示第 i 条特殊路径可以从 (x1i, y1i) 到 (x2i, y2i) ，但成本等于 costi 。你可以使用每条特殊路径任意次数。

返回从 (startX, startY) 到 (targetX, targetY) 所需的最小代价。

示例 1：

输入：start = [1,1], target = [4,5], specialRoads = [[1,2,3,3,2],[3,4,4,5,1]]
输出：5
解释：从 (1,1) 到 (4,5) 的最优路径如下：
- (1,1) -> (1,2) ，移动的代价是 |1 - 1| + |2 - 1| = 1 。
- (1,2) -> (3,3) ，移动使用第一条特殊路径，代价是 2 。
- (3,3) -> (3,4) ，移动的代价是 |3 - 3| + |4 - 3| = 1.
- (3,4) -> (4,5) ，移动使用第二条特殊路径，代价是 1 。
总代价是 1 + 2 + 1 + 1 = 5 。
可以证明无法以小于 5 的代价完成从 (1,1) 到 (4,5) 。

示例 2：

输入：start = [3,2], target = [5,7], specialRoads = [[3,2,3,4,4],[3,3,5,5,5],[3,4,5,6,6]]
输出：7
解释：最优路径是不使用任何特殊路径，直接以 |5 - 3| + |7 - 2| = 7 的代价从初始位置到达目标位置。

提示：

start.length == target.length == 2
1 <= startX <= targetX <= 105
1 <= startY <= targetY <= 105
1 <= specialRoads.length <= 200
specialRoads[i].length == 5
startX <= x1i, x2i <= targetX
startY <= y1i, y2i <= targetY
1 <= costi <= 105

网格图版求最短路径问题

题解：https://leetcode.cn/problems/minimum-cost-of-a-path-with-special-roads/solution/zhi-jie-qiu-zui-duan-lu-wu-xu-jian-tu-by-i8h7/

怎么想到的Dijkstra求解问题？

题目求的是源点到终点的最小代价，是最短路问题，由于每条路径长度不相同，因此不能用BFS，退而求其次使用Dijkstra

Dijkstra：每次选择一条最小代价的边，拿这一条边去更新别的边的最小代价

class Solution:
    """
    起点固定的单源最短路问题 ==> Dijkstra
        当不走特殊路径时，答案=起点到终点点的曼哈顿距离
        当走特殊路径时，答案时起点到特殊路径起点 + cost 走到特殊路路径终点
    
    抽象成一个图，一共有n + 2个点
    ==> 稠密图直接 O(n^2)遍历
    
    """
    def minimumCost(self, start: List[int], target: List[int], specialRoads: List[List[int]]) -> int:
        t = tuple(target) # pair
        dis = defaultdict(lambda: inf)
        dis[tuple(start)] = 0 # 起点为距离为0
        vis = set() 
        while True:
            v = None
            # 遍历所有最短路上的点
            for p, d in dis.items():
                # 如果这个点没有vis过 并且 这个点的距离是最小的
                if p not in vis and (v is None or d < dis[v]):
                    v = p
            if v == t: # 如果当前最小的点是终点，直接返回
                return dis[v]
            vis.add(v)
            vx, vy = v # 提出横坐标和纵坐标
            # 更新到终点的最短路(直接走曼哈顿距离)
            dis[t] = min(dis[t], dis[v] + abs(t[0] - vx) + abs(t[1] - vy)) 
                
            for x1, y1, x2, y2, cost in specialRoads: # 遍历所有特殊路径
                w = (x2, y2)
                # 走法1 ：(vx, vy) -> (x1, y1) -> 走特殊路径 -> (x2, y2) 
                #        abs(x1 -vx) + abs(y1 - vy) + cost
                # 走法2 ：(vx, vy) -> (x2, y2) 直接走到终点  
                #        abs(x2 - vx) + abs(y2 - vy)
                # 选择更小的走法
                d = dis[v] + min(abs(x2 - vx) + abs(y2 - vy), abs(x1 -vx) + abs(y1 - vy) + cost)
                dis[w] = min(dis[w], d)

java

class Solution {
    public int minimumCost(int[] start, int[] target, int[][] specialRoads) {
        long t = (long) target[0] << 32 | target[1];
        var dis = new HashMap<Long, Integer>();
        dis.put(t, Integer.MAX_VALUE);
        dis.put((long) start[0] << 32 | start[1], 0);
        var vis = new HashSet<Long>();
        for (;;) {
            long v = -1;
            int dv = -1;
            for (var e : dis.entrySet())
                if (!vis.contains(e.getKey()) && (dv < 0 || e.getValue() < dv)) {
                    v = e.getKey();
                    dv = e.getValue();                
                }
            if (v == t) return dv; // 到终点的最短路已确定
            vis.add(v);
            int vx = (int) (v >> 32), vy = (int) (v & Integer.MAX_VALUE);
            // 更新到终点的最短路
            dis.merge(t, dv + target[0] - vx + target[1] - vy, Math::min);
            for (var r : specialRoads) {
                int d = dv + Math.abs(r[0] - vx) + Math.abs(r[1] - vy) + r[4];
                long w = (long) r[2] << 32 | r[3];
                if (d < dis.getOrDefault(w, Integer.MAX_VALUE))
                    dis.put(w, d);
            }
        }
    }
}

2663. 字典序最小的美丽字符串

难度困难4

如果一个字符串满足以下条件，则称其为 美丽字符串 ：

它由英语小写字母表的前 k 个字母组成。
它不包含任何长度为 2 或更长的回文子字符串。

给你一个长度为 n 的美丽字符串 s 和一个正整数 k 。

请你找出并返回一个长度为 n 的美丽字符串，该字符串还满足：在字典序大于 s 的所有美丽字符串中字典序最小。如果不存在这样的字符串，则返回一个空字符串。

对于长度相同的两个字符串 a 和 b ，如果字符串 a 在与字符串 b 不同的第一个位置上的字符字典序更大，则字符串 a 的字典序大于字符串 b 。

例如，"abcd" 的字典序比 "abcc" 更大，因为在不同的第一个位置（第四个字符）上 d 的字典序大于 c 。

示例 1：

输入：s = "abcz", k = 26
输出："abda"
解释：字符串 "abda" 既是美丽字符串，又满足字典序大于 "abcz" 。
可以证明不存在字符串同时满足字典序大于 "abcz"、美丽字符串、字典序小于 "abda" 这三个条件。

示例 2：

输入：s = "dc", k = 4
输出：""
解释：可以证明，不存在既是美丽字符串，又字典序大于 "dc" 的字符串。

提示：

1 <= n == s.length <= 105
4 <= k <= 26
s 是一个美丽字符串

贪心

题解：https://leetcode.cn/problems/lexicographically-smallest-beautiful-string/solution/tan-xin-pythonjavacgo-by-endlesscheng-yix5/

class Solution:
    """
    它不包含任何长度为 2 或更长的回文子字符串。
    
    长度为6的回文串一定包含长度为4 为2的回文串
    贪心：只要保证不存在长度为2的回文串就不会有更长的回文串

    从右到左修改
    用进位的概念，把字符串看成一个k进制数
    """
    def smallestBeautifulString(self, s: str, k: int) -> str:
        a = ord('a')
        k += a
        s = list(map(ord, s))
        n = len(s)
        i = n - 1
        s[i] += 1  # 从最后一个字母开始
        while i < n:
            if s[i] == k:  # 超过范围
                if i == 0: return ""  # 无法进位
                # 进位
                s[i] = a
                i -= 1 # 有限解决前面的回文串
                s[i] += 1
            # 讨论长为 2 和长为 3 的回文串的情况，继续累加
            elif i and s[i] == s[i - 1] or i > 1 and s[i] == s[i - 2]:
                s[i] += 1  # 如果 s[i] 和前面的字符形成回文串，就继续增加 s[i]
            else:
                i += 1  # 检查 s[i] 是否和后面的字符形成回文串
        return ''.join(map(chr, s))

“” # 无法进位
# 进位
s[i] = a
i -= 1 # 有限解决前面的回文串
s[i] += 1
# 讨论长为 2 和长为 3 的回文串的情况，继续累加
elif i and s[i] == s[i - 1] or i > 1 and s[i] == s[i - 2]:
s[i] += 1 # 如果 s[i] 和前面的字符形成回文串，就继续增加 s[i]
else:
i += 1 # 检查 s[i] 是否和后面的字符形成回文串
return ‘’.join(map(chr, s))