AtCoder Beginner Contest 300（D-G）

news2024/12/28 9:01:22

D - AABCC (atcoder.jp)

        （1）题目大意

                给你个数N，问你不超过N的三个质数abc组成的数有多少个。

         （2）解题思路

                考虑到枚举的数不会特别多，因此预处理出1e6的质因子，暴力枚举即可。

         （3）代码实现

#include<bits/stdc++.h>
#define sz(x) (int) x.size()
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 1e6 + 10;
struct Primes {
    bitset <N> st;
    int cnt,primes[N],idx[N],n;
 
    Primes(int n = N - 1) {
        this->n = n;
        init(n);
    }
 
    void init(int n) {
        st[0] = st[1] = 1;
        for(int i = 2;i <= n;i ++) {
            if(!st[i]) {
                primes[++ cnt] = i;
                idx[i] = cnt;
            }
            for(int j = 1;primes[j] <= n / i;j ++) {
                st.flip(primes[j] * i);
                if(i % primes[j] == 0) break;
            }
        }
    }
    
    //判断x是否是质数      
    bool isPrime(int x) {
        assert(x <= n);
        return !st[x];
    }
    
    //求解x在质数表是第几个                    
    bool atIndex(int x) {
        assert(!st[x]);
        assert(x <= n);
        return idx[x];
    }
};
using i128 = __int128;
void solve(){
	ll n;
	cin >> n;
	Primes pr(1e6);
	vector <int> v;
	for(int i = 1;i <= 1e6;i ++) {
		if(pr.isPrime(i)) v.pb(i);
	}
	int cnt = 0,siz = sz(v);
	for(int i = 0;i < siz;i ++) {
		ll v1 = 1ll * v[i] * v[i];
		if(v1 > n) break;
		for(int j = i + 1;j < siz;j ++) {
			i128 v2 = (i128) 1 * v[j];
			if((i128) 1ll * v1 * v2 > n) break;
			for(int k = j + 1;k < siz;k ++) {
				i128 v3 = 1ll * v[k] * v[k];
                if((i128) v1 * v2 * v3 > n) break;
				cnt ++;
			}
		}
	}
	cout << cnt << endl;
}

int main()
{
    ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	int T = 1;
//	cin >> T;
	while(T --) solve();
}

E - Dice Product 3 (atcoder.jp)

        （1）题目大意

                给你一个数N，然后给你一个初始数1，每次你可以摇一下骰子，摇到多少把当前的数乘上多少，问你最后变成N的概率是多少？

         （2）解题思路

                观察题目，考虑1没用，我们可以直接dp[i][j][k]表示2还剩i次，3还剩j次，5还剩k次的概率，因为4和6可以用2和3表示出来，因此我们考虑把N质因子分解，然后倒着dp即可。

                需要注意的是每一次只需要乘上1/5的概率。

                解释：考虑当前数为n

                        f(n) = \frac{1}{6}(f(n)+f(2n)+f(3n)+f(4n)+f(5n)+f(6n))

                移项可得

                ​​​​​​​        \frac{5}{6}f(n) = \frac{1}{6}(f(2n)+f(3n)+f(4n)+f(5n)+f(6n))

                        f(n) = \frac{1}{5}(f(2n)+f(3n)+f(4n)+f(5n)+f(6n))

         （3）代码实现

#include<bits/stdc++.h>
#define sz(x) (int) x.size()
#define PII pair<int,int>
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define all(x) (x).begin(),(x).end()
#define rep(i, j, k) for (int i = (j); i <= (k); ++i)
#define per(i, j, k) for (int i = (j); i >= (k); --i)
#define SZ(v) int((v).size())
#define ALL(v) (v).begin(),(v).end()
#define fi first
#define se second
#define gc getchar
#define pc putchar
using namespace std;
using ll = long long;
using pii = std::pair<int, int>;
using pll = std::pair<ll, ll>;
using namespace std;
const ll mod = 998244353;
ll ksm(ll a,ll b)
{
	ll res = 1;
	while(b) {
		if(b & 1) res = res * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return res;
}
template <class T = int> T read() {
  T x = 0; bool f = 0; char ch = gc();
  while (!isdigit(ch)) f = ch == '-', ch = gc();
  while (isdigit(ch)) x = (x << 3) + (x << 1) + (ch ^ 48), ch = gc();
  return f ? -x: x;
}
template <class T> void write(T x) {
  if (x >= 0) { if (x > 9) write(x / 10); pc(x % 10 + 48); }
  else { pc('-'); if (x < -9) write(-x / 10); pc(48 - x % 10); }
}

namespace pr {
  mt19937_64 rnd(random_device{}());
  using ull = unsigned long long;
  using u128 = unsigned __int128;
  
  struct barrett_64 {
    ull mod, r;
    u128 k;
    barrett_64(ull _mod) {
      mod = _mod;
      r = __lg(mod);
      if ((1ull << r) < mod) r++;
      k = ((r == 64 ? u128(0) : u128(1) << r * 2) - 1) / mod + 1;
    }
    ull mul(ull a, ull b) {
      u128 c = ((u128(a) * b >> r) * k) >> r;
      if (c) c--;
      u128 d = u128(a) * b - u128(c) * mod;
      while (d >= mod) d -= mod;
      return d;
    }
    ull sub(ull a, ull b) { return a < b ? a - b + mod : a - b; }
    ull add(ull a, ull b) { return sub(a, mod - b); }
  } reducer(1);
  
  ull gcd(ull a, ull b) { return b ? gcd(b, a % b) : a; }
  ull qpow(ull a, ull b) {
    ull res(1);
    for (; b; b >>= 1, a = reducer.mul(a, a))
      if (b & 1) res = reducer.mul(res, a);
    return res;
  }
  bool is_prime(ull n) {
    if (n <= 1) return false;
    vector<ull> base = {2, 3, 5, 7, 11, 13, 17, 19, 23};
    for (ull p : base) {
      if (n == p) return true;
      if (n % p == 0) return false;
    } 
    reducer = barrett_64(n);
    ull m = (n - 1) >> __builtin_ctz(n - 1);
    for (ull p : base) {
      ull t = m, a = qpow(p, m);
      while (t != n - 1 && a != 1 && a != n - 1)
        a = reducer.mul(a, a), t *= 2;
      if (a != n - 1 && t % 2 == 0) return false;
    }
    return true;
  }
  ull get_factor(ull n) {
    if (n % 2 == 0) return 2;
    reducer = barrett_64(n);
    auto f = [&](ull x) { return reducer.add(reducer.mul(x, x), 1); };
    ull x = 0, y = 0, tot = 0, p = 1, q, g;
    for (ull i = 0; (i & 0xff) || (g = gcd(p, n)) == 1; i++) {
      if (x == y) {
        x = tot, y = f(x);
        if (++tot == n) tot = 0;
      }
      q = reducer.mul(p, reducer.sub(x, y));
      if (q) p = q;
      x = f(x), y = f(f(y));
    }
    return g;
  }
  
  vector<ull> solve(ull n) {
    if (n == 1) return {};
    if (is_prime(n)) return {n};
    ull d = get_factor(n);
    auto v1 = solve(d), v2 = solve(n / d);
    auto i1 = v1.begin(), i2 = v2.begin();
    vector<ull> ans;
    while (i1 != v1.end() || i2 != v2.end()) {
      if (i1 == v1.end()) ans.push_back(*i2++);
      else if (i2 == v2.end()) ans.push_back(*i1++);
      else {
        if (*i1 < *i2) ans.push_back(*i1++);
        else ans.push_back(*i2++);
      }
    }
    return ans;
  }
}
using i64 = long long;

constexpr int P = 998244353;
// assume -P <= x < 2P
int Vnorm(int x) {
    if (x < 0) {
        x += P;
    }
    if (x >= P) {
        x -= P;
    }
    return x;
}
template<class T>
T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}
struct Mint {
    int x;
    Mint(int x = 0) : x(Vnorm(x)) {}
    Mint(i64 x) : x(Vnorm(x % P)) {}
    int val() const {
        return x;
    }
    Mint operator-() const {
        return Mint(Vnorm(P - x));
    }
    Mint inv() const {
        assert(x != 0);
        return power(*this, P - 2);
    }
    Mint &operator*=(const Mint &rhs) {
        x = i64(x) * rhs.x % P;
        return *this;
    }
    Mint &operator+=(const Mint &rhs) {
        x = Vnorm(x + rhs.x);
        return *this;
    }
    Mint &operator-=(const Mint &rhs) {
        x = Vnorm(x - rhs.x);
        return *this;
    }
    Mint &operator/=(const Mint &rhs) {
        return *this *= rhs.inv();
    }
    friend Mint operator*(const Mint &lhs, const Mint &rhs) {
        Mint res = lhs;
        res *= rhs;
        return res;
    }
    friend Mint operator+(const Mint &lhs, const Mint &rhs) {
        Mint res = lhs;
        res += rhs;
        return res;
    }
    friend Mint operator-(const Mint &lhs, const Mint &rhs) {
        Mint res = lhs;
        res -= rhs;
        return res;
    }
    friend Mint operator/(const Mint &lhs, const Mint &rhs) {
        Mint res = lhs;
        res /= rhs;
        return res;
    }
    friend std::istream &operator>>(std::istream &is, Mint &a) {
        i64 v;
        is >> v;
        a = Mint(v);
        return is;
    }
    friend std::ostream &operator<<(std::ostream &os, const Mint &a) {
        return os << a.val();
    }
};
Mint dp[63][63][63];
int have[4];
void solve(){
	ll n;
	cin >> n;
	auto f = pr::solve(n);
	if(f.back() >= 7) {
		cout << 0 << endl;
		return;
	}
	for(auto x : f) {
		if(x == 2) have[1] ++;
		if(x == 3) have[2] ++;
		if(x == 5) have[3] ++;
	}
	dp[have[1]][have[2]][have[3]] = 1;
  	ll tv = ksm(5,P - 2);
  	int a = have[1],b = have[2],c = have[3];
	for(int i = a;i >= 0;i --) {
		for(int j = b;j >= 0;j --) {
			for(int k = c;k >= 0;k --) {
              	if(i == a && j == b && k == c) continue;
				if(i + 1 <= a) dp[i][j][k] += dp[i + 1][j][k];
              	if(j + 1 <= b) dp[i][j][k] += dp[i][j + 1][k]; 
				if(k + 1 <= c) dp[i][j][k] += dp[i][j][k + 1];
				if(i + 2 <= a) dp[i][j][k] += dp[i + 2][j][k];
				if(i + 1 <= a && j + 1 <= b) dp[i][j][k] += dp[i + 1][j + 1][k];
				dp[i][j][k] *= tv;
			}
		}
	}
	cout << dp[0][0][0] << endl;
}

int main()
{
    ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	int T = 1;
//	cin >> T;
	while(T --) solve();
}

  F - More Holidays (atcoder.jp)               

             （1）题目大意

                        给你一次长度为N的字符串S，然后复制了M遍，问你可以一定把K个x变成o，问你最大的连续o的长度为多少？   

         （2）解题思路

                考虑前缀和预处理出每一个x的位置，然后枚举在这些x的位置开始改k次，O1即可算出来改了K个之后的位置，以及答案是多少。

         （3）代码实现

#include<bits/stdc++.h>
#define sz(x) (int) x.size()
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
void solve(){
	ll n,m,k;
	string s;
	cin >> n >> m >> k;
	cin >> s;
	vector<int> p;
	for(int i = 0;i < n;i ++) {
		if(s[i] == 'x') p.pb(i);
	}
	auto get = [&](ll k) {
		ll rp = p[k % sz(p)] + k / sz(p) * n;
		return min(rp,n * m);
	};
	ll ans = get(k);
	for(int i = 0;i < sz(p);i ++) ans = max(ans,get(i + k + 1) - p[i] - 1);
	cout << ans << '\n';
}

int main()
{
    ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	int T = 1;
//	cin >> T;
	while(T --) solve();
}

G - P-smooth number (atcoder.jp)

        （1）题目大意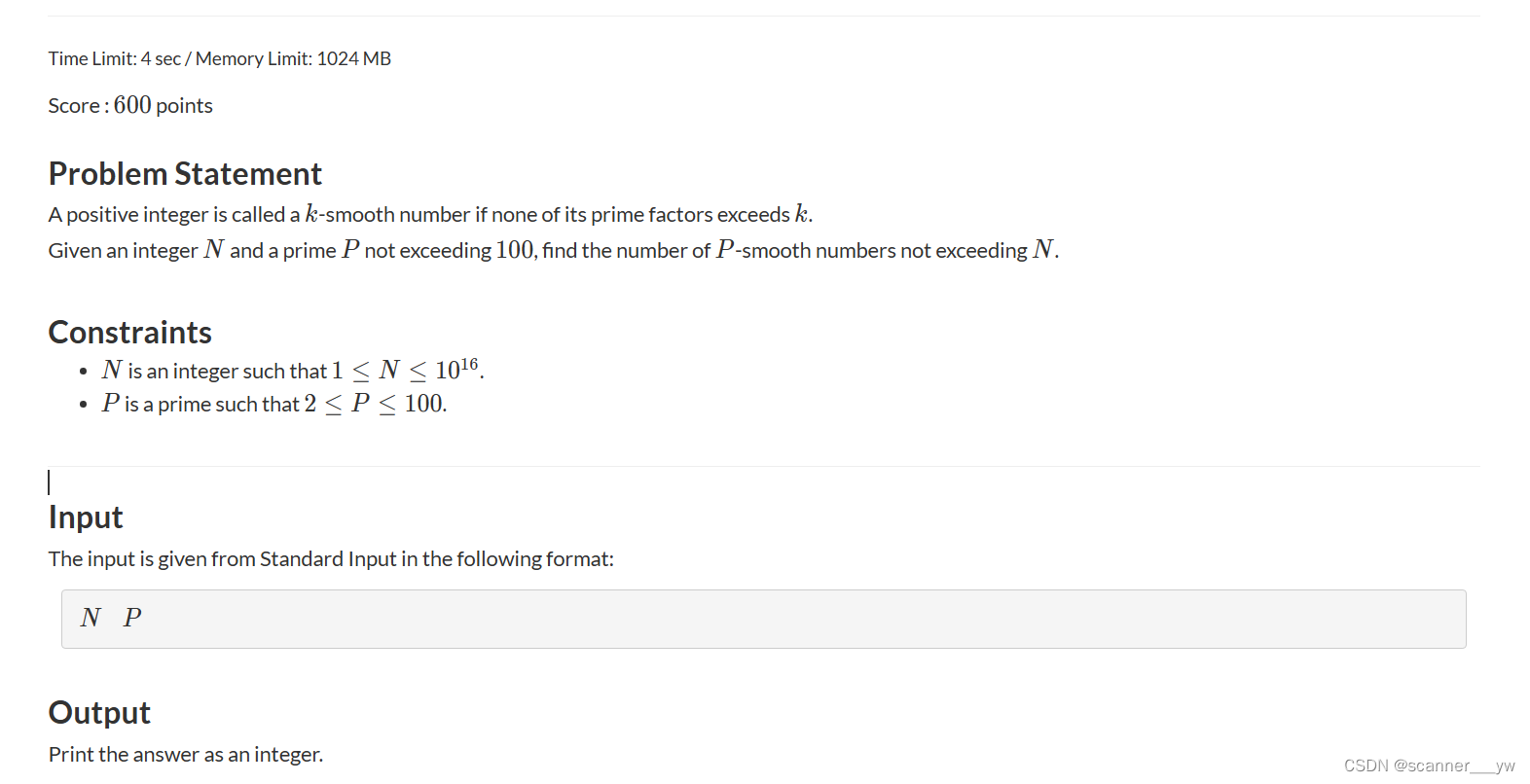

         （2）解题思路

                用两个数组存下来前半部分的素数乘和后半部分的素数乘出来的数，然后排个序，枚举第一个数组，然后第二个数组用双指针扫一下计算贡献即可。

         （3）代码实现

#include<bits/stdc++.h>
#define sz(x) (int) x.size()
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
struct Primes {
    bitset <N> st;
    int cnt,primes[N],idx[N],n;
 
    Primes(int n = N - 1) {
        this->n = n;
        init(n);
    }
 
    void init(int n) {
        st[0] = st[1] = 1;
        for(int i = 2;i <= n;i ++) {
            if(!st[i]) {
                primes[++ cnt] = i;
                idx[i] = cnt;
            }
            for(int j = 1;primes[j] <= n / i;j ++) {
                st.flip(primes[j] * i);
                if(i % primes[j] == 0) break;
            }
        }
    }
    
    //判断x是否是质数      
    bool isPrime(int x) {
        assert(x <= n);
        return !st[x];
    }
    
    //求解x在质数表是第几个                    
    bool atIndex(int x) {
        assert(!st[x]);
        assert(x <= n);
        return idx[x];
    }
}pr(100);
ll n,p;
void dfs(vector<ll> &a,int z)
{
	for(int i = 0;i < sz(a);i ++) {
		if(a[i] * z < n) {
			a.pb(a[i] * z);
		}
	}
}
void solve(){
	cin >> n >> p;
	vector<int> f;
	for(int i = 1;i <= p;i ++) {
		if(pr.isPrime(i)) f.pb(i); 
	}
	vector<ll> v1,v2;
	v1.pb(1),v2.pb(1);
	for(int i = 0;i < sz(f);i ++) {
		if(sz(v1) < sz(v2)) dfs(v1,f[i]);
		else dfs(v2,f[i]);
	}
	sort(all(v1));
	sort(all(v2));
	int j = sz(v2) - 1;
	ll ans = 0;
	for(int i = 0;i < sz(v1);i ++) {
		ll pv = n / v1[i];
		while(j >= 0 && v2[j] > pv) j --;
		ans += j + 1;
	}
	cout << ans << endl;
}

int main()
{
    ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	int T = 1;
//	cin >> T;
	while(T --) solve();
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/480954.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

在体育新闻文本中提取关键词可以使用什么技术

在体育新闻文本中提取关键词可以使用什么技术

在体育新闻文本中提取关键词可以使用以下技术&#xff1a; 1. 领域词典&#xff1a; 通过构建体育领域的词汇表&#xff0c;将其中的词语作为关键词&#xff0c;可以较好地提取体育新闻中的关键词。 就当下的研究情况&#xff0c;国内外有哪些体育领域的词汇表http://t.csdn…
阅读更多...
Reactive Streams介绍与应用分析

Reactive Streams介绍与应用分析

目录 一、Reactive Streams基本知识 &#xff08;一&#xff09;基本介绍 &#xff08;二&#xff09;反应式流的特点 基本特性1:事件驱动&变化传递 基本特性2:数据流 基本特性3:声明式 高级特性1:流量控制&#xff08;回压&#xff09; 高级特性2:异步边界 &…
阅读更多...
ALBEF：基于动量蒸馏的视觉语言表示学习

ALBEF：基于动量蒸馏的视觉语言表示学习

Align before Fuse&#xff1a;Vision and Language Representation Learning with Momentum Distillation ALBEF&#xff1a;基于动量蒸馏的视觉语言表示学习 摘要 大规模的视觉和语言表征学习在各种视觉-语言任务上显示出有希望的改进。大多数现有的方法采用了基于Transform…
阅读更多...
【平衡二叉搜索树（AVL）-- 旋转】

【平衡二叉搜索树（AVL）-- 旋转】

目录&#xff1a; 前言1、二叉搜索树的插入2、AVL树的旋转&#xff08;1&#xff09;右单旋&#xff08;LL&#xff09;&#xff08;2&#xff09;左单旋&#xff08;RR&#xff09;&#xff08;3&#xff09;右左双旋&#xff08;LR&#xff09;&#xff08;4&#xff09;左右…
阅读更多...
第18章 项目风险管理

第18章 项目风险管理

文章目录 18.1.2 风险的分类 54318.1.3 风险的性质 544项目风险管理6个过程&#xff08;风险管理、识别风险、实施定性风险分析、实施定量风险分析、规划风险应对、控制风险&#xff09;组织和干系人的风险态度影响因素18.3.3 规划风险管理的输出 550风险识别的原则18.4.2 识别…
阅读更多...
vim编辑文件

vim编辑文件

目录 一、vi和vim &#xff08;1&#xff09;介绍 &#xff08;2&#xff09;相同点 &#xff08;3&#xff09;不同点 二、使用vim打开文件 三、使用vim编辑文件 &#xff08;1&#xff09;vim的四个模式 &#xff08;2&#xff09;命令模式下的编辑命令 删除 复制 …
阅读更多...
树莓派4：跑通Tensorflow的Sequential模型用于图片分类

树莓派4：跑通Tensorflow的Sequential模型用于图片分类

重要提示&#xff1a;由于树莓派相对孱弱的性能&#xff0c;直接在其上训练模型可能花&#xff08;lang4&#xff09;费非常长的时间。本文仅作为示例性的可行性参考&#xff0c;请酌情考虑实验平台。 著名的Tensorflow框架也可以运行在树莓派上。理论还没吃透&#xff0c;但使…
阅读更多...
【量化交易笔记】5.SMA，EMA 和WMA区别

【量化交易笔记】5.SMA，EMA 和WMA区别

股票中的SMA&#xff0c;EMA和WMA是常用的技术分析指标。这些指标基于历史股价计算得出&#xff0c;可以帮助投资者了解股票的趋势&#xff0c;为决策提供依据。虽然它们都是平均值算法&#xff0c;但它们之间还是有一些区别的。 SMA 简单移动平均线&#xff08;Simple Moving…
阅读更多...
参与辅助服务的用户侧储能优化配置及经济分析（matlab代码）

参与辅助服务的用户侧储能优化配置及经济分析（matlab代码）

目录 1 主要内容 目标函数 2 部分程序 3 程序结果 4 程序链接 1 主要内容 该程序方法复现《参与辅助服务的用户侧储能优化配置及经济分析》&#xff0c;首先&#xff0c; 建立了用户侧储能的全生命周期成本和考虑辅助服务的收益模型&#xff1b;其次&#xff0c;在两部…
阅读更多...
一文读懂UML用例图

一文读懂UML用例图

一、概述 用例是描述系统需求的一种手段&#xff0c;即系统应该做什么。用例图由参与者、用例和主题组成。每个用例的主题都代表了一个用例所适用的系统。用户和任何其他可以与主体交互的系统都被表示为行动者。 用例是一种行为规范。用例的实例指的是紧急行为的发生符合相应…
阅读更多...
【前端客栈】基于HTML、CSS、JavaScript的羊了个羊静态仿写页面小游戏

【前端客栈】基于HTML、CSS、JavaScript的羊了个羊静态仿写页面小游戏

&#x1f3dc;哈喽&#xff0c;大家好&#xff0c;我是小浪。前段时间羊了个羊火遍了大江南北&#xff0c;大家是否都通过第二关了呢&#xff1f;哈哈&#xff0c;没关系&#xff0c;既然通不过&#xff0c;那咋们不如自己来做一个这样的羊了个羊的仿写页面&#xff0c;学会了赶…
阅读更多...
文本中的关键词提取方法

文本中的关键词提取方法

目录 1. TF-IDF&#xff08;Term Frequency-Inverse Document Frequency&#xff09;算法&#xff1a; 2. TextRank算法&#xff1a; 3. LDA&#xff08;Latent Dirichlet Allocation&#xff09;算法&#xff1a; 4. RAKE&#xff08;Rapid Automatic Keyword Extraction&…
阅读更多...
基于SLM调制器，MIT研发高效率全息显示方案

基于SLM调制器，MIT研发高效率全息显示方案

此前&#xff0c;青亭网曾报道过NVIDIA、三星、剑桥大学等对空间光调制器&#xff08;SLM&#xff09;全息方案的探索。空间光调制器可调节光波的空间分布&#xff0c;在电驱动信号控制下&#xff0c;可改变光在空间中传播的振幅、强度、相位、偏振态等特性&#xff0c;从而形成…
阅读更多...
MySQL性能优化之（explain）工具

MySQL性能优化之（explain）工具

慢SQL的定位 在MySQL当中&#xff0c;我们有时候写的SQL执行效率太慢此时我们需要将其优化。但是SQL可能非常的多&#xff0c;难道我们一条一条的进行查看吗&#xff1f;在MySQL当当中我们可以查看慢查询日志&#xff0c;看看那些SQL这么慢。但是这个默认情况下这个慢查询日志…
阅读更多...
sqoop使用

sqoop使用

sqoop使用 1. 导入数据2. 从mysql向hive导入数据2.1 导入用户信息表 2.导入订单表2.2 导入订单表2.3 导入商品信息表2.4 导入国家信息表2.5 导入省份信息表2.6 导入城市信息表2.7 创建hive临时表文件 在使用sqoop之前&#xff0c;需要提前启动hadoop, yarn和对应的数据库mysql …
阅读更多...
当音乐遇上Python：用Pydub自动分割音频

当音乐遇上Python：用Pydub自动分割音频

&#x1f3b5; &#x1f3b5; &#x1f3b5; 当音乐遇上Python&#xff1a;用Pydub自动分割音频 随着短视频应用的普及&#xff0c;越来越多人开始了解并尝试制作自己的短视频作品。而在制作短视频时&#xff0c;背景音乐的选择和使用也是非常重要的一步。很多人喜欢选择一首长…
阅读更多...
倒立摆控制器的设计（分别用极点配置，LQR方法，Robust H-无穷方法）

倒立摆控制器的设计（分别用极点配置，LQR方法，Robust H-无穷方法）

G01倒立摆控制器设计 Author&#xff1a;DargonNote date&#xff1a;2020/12/13课程用书&#xff1a;LMIs in Control Systems Analysis,Design and Applications 1,倒立摆控制系统简介 倒立摆系统是一个复杂的控制系统&#xff0c;具有非线性、强耦合、多变量、不稳定等特…
阅读更多...
文法和语言的形式定义——最左最右推导、归约、递归

文法和语言的形式定义——最左最右推导、归约、递归

最左最右推导 归约 递归
阅读更多...
干货 | 正念，寻求属于你的存在之道

干货 | 正念，寻求属于你的存在之道

Hello,大家好&#xff01; 这里是壹脑云科研圈&#xff0c;我是喵君姐姐~ 你是否也曾感到内心无法平静&#xff1f;如果是&#xff0c;不妨了解一下正念&#xff0c;它或许能为你带来改变。 正念作为一种古老的修行方式&#xff0c;如今已经在世界范围内广为流传&#xff0c;…
阅读更多...
《Netty》从零开始学netty源码（四十九）之PoolArena

《Netty》从零开始学netty源码（四十九）之PoolArena

目录 PoolArenaallocate()创建newByteBuf()分配具体的内存空间allocate() PoolArena Netty中分配内存是委托给PoolArena来管理的&#xff0c;它主要有两个实现类&#xff1a; 默认情况下使用的DirectArena&#xff0c;它的数据结构如下&#xff1a; 从属性中我们看到PoolA…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023