G01倒立摆控制器设计

Author：Dargon
Note date：2020/12/13
课程用书：LMIs in Control Systems Analysis,Design and Applications

1,倒立摆控制系统简介

倒立摆系统是一个复杂的控制系统，具有非线性、强耦合、多变量、不稳定等特性。在控制过程中, 它能有效的反映控制中的许多关键问题，如镇定问题,非线性问题, 鲁棒性问题, 随动问题及跟踪问题恩等，都可以以倒立摆为对象加以研究。除此之外, 它和火箭的飞行及机器人关节运动有很多相似之处，其原理可用于控制火箭稳定发射。倒立摆的研究对于火箭飞行控制和机器人控制等现代高科技的研究具有重要的实践意义。因此倒立摆的控制成为控制理论中经久不衰的研究课题。在最近的 25 年里，许多经典和现代控制理论被用于倒立摆的稳定控制，例如极点配置控制、LQR控制、状态反馈控制、鲁棒 $H_{\infty}$ 、智能控制、模糊控制、人工神经元控制。
从形式上可以将倒立摆系统分为以下几种：
1. 直线倒立摆系统：或称为“小车-倒立摆系统”,是由可以沿直线导轨运动的小车及一端定于小车之上的匀质长杆组成的系统。
2. 环形倒立摆系统：可以将它看成是将小车的直线导轨弯曲而成的系统。
3. 平面倒立摆系统：匀质摆杆的底端可以在平面内自由运动,并且摆杆可以沿平面内的任一轴线转动。
4. 柔性连接倒立摆系统：在原倒立摆系统的基础之上引入了新的自由振荡环节:自由弹簧系统。
5. 柔性倒立摆系统：它不仅仅是将匀质刚体换成了柔性摆杆,而是其本身已经变为非线性分布参数系统。
6. 直线柔性连接两级倒立摆：所谓直线柔性连接两级倒立摆系统,就是在直线刚性两级倒立摆的基础上,加入自由弹簧系统:电机连接一主动小车,而主动小车通过一根弹簧作用于从动小车,对固定于从动小车上的两级倒立摆实施控制。

2，倒立摆数学模型的分析与建立

2.1，模型分析

倒立摆系统如图1所示，一个带轮的小车，中间铰接刚性的倒立摆，小车沿着笔直的光滑轨道左右滑动，同事实现的摆杆可在垂直平面内自由运动，为方便分析，我们假设摩擦力都是足够的小，可以忽略不计。由动力学理论可推出一级倒立摆的运动方程。

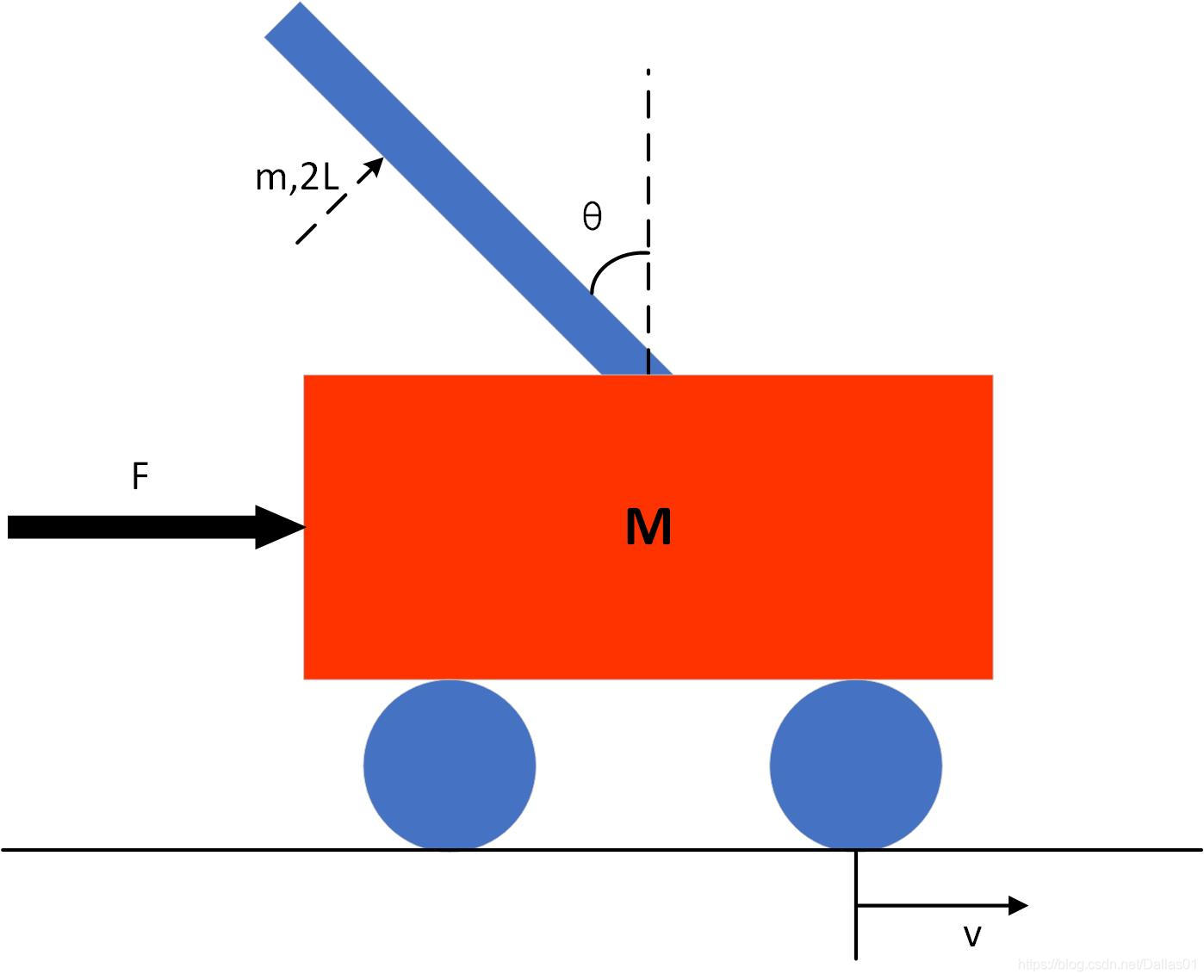
M：小车的质量
m：摆杆的质量
L：摆杆质心到转轴的距离
I：摆杆的转动惯量
g: 重力加速度
b：小车与导轨之间的阻尼比
C: 摆杆与小车之间的阻尼比
$\theta$ : 摆杆与竖直方向上的夹角
F：控制器的输出的外力

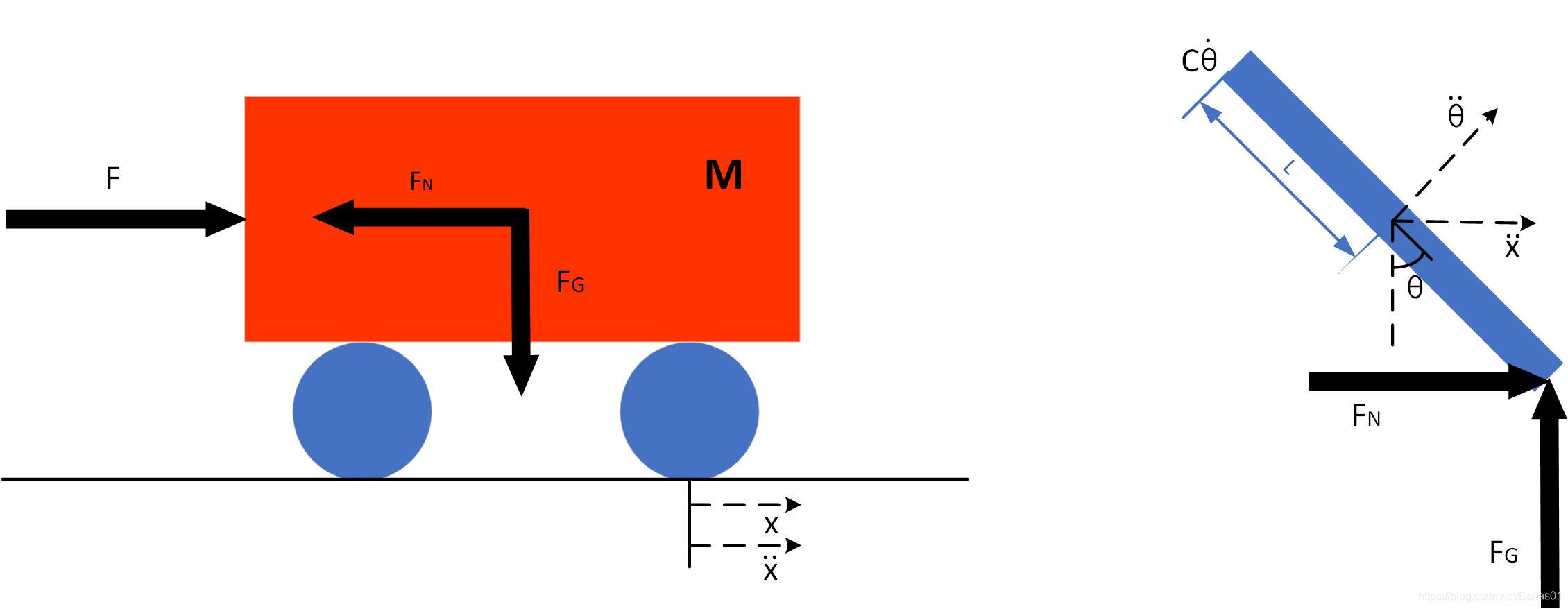
小车水平方向受力
$M\ddot{x} =F -F_N -b \dot{x} \tag{2.1}$
摆杆的水平受力
$F_N =m \frac{d^{2}(x +Lsin\theta)}{dt^2} \tag{2.2}$
根据公式（2.1）、（2.2）可获得系统的一个运动学方程
$\ddot{x} +mL\ddot{\theta}cos\theta -mL \dot{\theta}^{2}sin\theta +b \dot{x}\tag{2.3}$
摆杆的垂直方向受力
$F_P -mg =m \frac{d^2(Lcos \theta)}{dt^2} \tag{2.4}$
力矩平衡
$I\ddot{\theta} =F_PLsin\theta -F_NLcos\theta -c \dot{\theta} \tag{2.5}$
将（2.2）和（2.4）分别代入（2.5）得出系统的另一个方程
$+mL^2) \ddot{\theta} +mL \ddot{x} +c\dot{\theta} =mgL\theta \tag{2.6}$
将系统线性化令 $sin\theta \approx \theta, cos\theta \approx 1,(\frac{d\theta}{dt})^2 =0$ 得出
$\left\{ \begin{aligned} F&=(M +m) \ddot{x} +mL \ddot{\theta} +b \dot{x}\\ mgL\theta &=(I +mL^2) \ddot{\theta} +mL \ddot{x} +c \dot{\theta} \end{aligned} \right. \tag{2.7}$

2.2,系统状态方程建模

在任意时刻，系统的状态都由4个变量来描述，分别是摆杆的角度 $\theta$ ,摆杆的角速度 $\dot{\theta}$ ,小车的位移 $x$ ,小车的速度 $\dot{x}$
令 $\quad \dot{x} \quad \theta \quad \dot{\theta} ]}^T$ , $\quad \dot{x} \quad \theta \quad \dot{\theta} ]}^T$
可以描述系统的状态空间方程
$\left\{ \begin{aligned} \dot{X} &=AX +BU\\ Y &=CX +DU \end{aligned} \right. \tag{2.8}$
$=\left[ \begin{matrix} 0 & 1& 0& 0\\ 0 &a_1&a_2&a_3\\ 0 & 0& 0& 1\\ 0 &a_4&a_5&a_6 \end{matrix} \right] B =\left[ \begin{matrix} 0 \\ b_1\\ 0 \\ b_2 \end{matrix} \right] C =\left[ \begin{matrix} 1 & 0& 0& 0\\ 0& 1& 0& 0\\ 0 & 0& 1& 0\\ 0& 0& 0& 1 \end{matrix} \right] D =\left[ \begin{matrix} 0 \\ 0\\ 0 \\ 0 \end{matrix} \right]$
其中 $a_1 =\frac{-b(I +mL^2)}{(M +m)I +MmL^2} \quad a_2 =\frac{-m^2L^2g }{(M +m)I +MmL^2} \quad a_3 =\frac{mLc}{(M +m)I +MmL^2}$
$a_4 =\frac{mLb}{(M +m)I +MmL^2} \quad a_5 =\frac{mgL(M +m) }{(M +m)I +MmL^2} \quad a_6 =\frac{-c(M +m)}{(M +m)I +MmL^2}$
$b_1 =\frac{I +mL^2}{(M +m)I +MmL^2} \quad b_2 =\frac{-mL }{(M +m)I +MmL^2}$

3,控制器的设计

3.1 无控制器

对于无控制器的情况，我们判断A的稳定性即可
$\quad 0.0830\quad -5.2780 \quad 502726]$
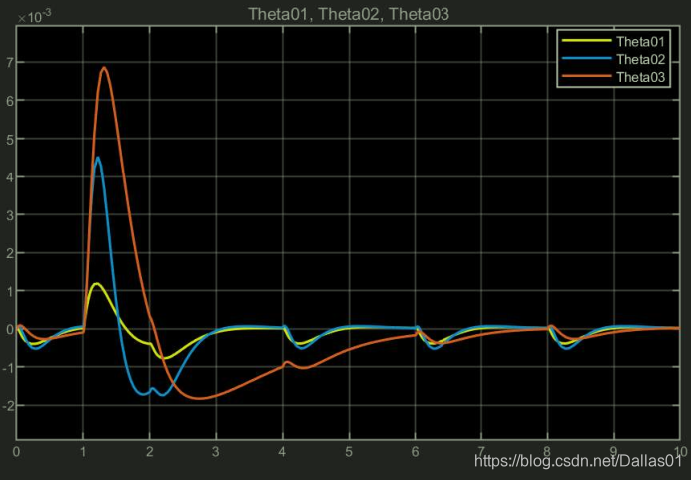
对于特征值有在右半平面的情况，系统是不稳定的，可见其图像是发散的

%---------------------------------without control-------------------
disp(eig(A));
The eigenvalue of A :
    0
-0.0830
-5.2780
5.2726

3.2 极点配置设计控制器

利用matlab，将极点全部配置在左半平面内，设置的极点 $\quad -9 \quad -1 \quad -0.5]$ ,利用的matlab的place函数，进行配置求解反馈增益K的值。

%---------------------------------pole placement---------------------
disp('Pole placement');
P=[-10,-9,-1,-1.5];
K=place(A,B2,P);
disp('Feedback gain K:');
disp(K);

Pole placement
Feedback gain K:
   -5.8454  -11.0766   72.9832   13.2371

3.3 LQR方法设计控制器

利用matlab找到最优的极点配置，对于是得二次型的代价函数（Cost function）最小，同时，设置对应的权重矩阵Q 和R
$=\int_0^{\infty}(X^TQX +U^TRU)dt$
利用matlab对应的LQR求解函数 lqr可求其解

%--------------------------------LQR controll---------------------------
disp('LQR control');
Q=[200 0 0   0;
     0 1 0   0;
     0 0 200 0;
     0 0 0   1];
R=0.1;
[K,P,E] =lqr(A,B2,Q,R);
disp('Feedback gain K:');
disp(K);
disp('The eigenvalue:');
disp(E);

LQR control
Feedback gain K:
  -44.7214  -31.5945  119.3920   21.7285

The eigenvalue:
  -9.2460 + 5.3810i
  -9.2460 - 5.3810i
  -2.4487 + 1.7404i
  -2.4487 - 1.7404i

3.4 Robust $H_\infty$ 设计控制器

利用matlab里面的LMI toolbox去解决关于鲁棒 $H_\infty$ 的求解控制问题，对于 $H_\infty$ 是由明确的数学推导和物理意义的，关于欧拉范数的推导出矩阵谱范数（2范数）形式，属于定常矩阵的形式，对于 $H_\infty$ 范数是由2范数进行推广的，完全可以利用导出范数，去定义 $H_\infty$ 形式。就可以看出如果输入时扰动的话，就代表这一种放大倍数 $\gamma$ ，当然我们的目标就是要是 $\gamma$ 越小越好。
求 $H_\infty$ 问题可以写成以下标准形式求解问题：
$\quad \gamma$
$\quad to :$
$\left\{ \begin{aligned} \left[ \begin{matrix} AX +B_2W+(AX +B_2W)^T & B_1& (C_1X +D_{12}W)^T)\\ {B_1}^T &-I &D_{11}^T\\ C_1X +D_{12}W &D_{11}&-{\gamma}^2I \end{matrix} \right] <0\\ X >0 \end{aligned} \right. \tag{3.1}$

$u = K x$
所求得的 $K =WX^{-1}$
利用matlab LMI toolbox的feasp 函数去求可行性问题，利用mincx 去求最小的 $\gamma$
所求得的最小的 $\gamma =0.8834$

%descripe LMI
setlmis([]);       %建立一个LMI
X=lmivar(1,[4,1]); %定义矩阵变量
W=lmivar(2,[1,4]);
r1=lmivar(1,[1,1]);

% The first inequation
lmiterm([1 1 1 X],A,1,'s'); %AX +(AX)'
lmiterm([1 1 1 W],B2,1,'s'); %B2W +(B2W)'
lmiterm([1 2 1 0],B1'); %B1
lmiterm([1 2 2 0],-1); %-I
lmiterm([1 3 1 X],C1,1); %C1X +D12W
lmiterm([1 3 1 W],D12,1);
lmiterm([1 3 2 0],D11); %D11
lmiterm([1 3 3 r1],-1,1); %-r^2 *I

% The second equation
lmiterm([-2 1 1 X],1,1); %X >0

lmisys=getlmis;

%----------------------------Robust mincx solver---------------------------------------

n = decnbr(lmisys);
c = zeros(n,1);
for j=1:n
     [r1j]=defcx(lmisys,j,r1);
      c(j)=trace(r1j);
end
%c=mat2dec(lmisys,zeros(4,4),zeros(1,4),eye(1))
[copt,xopt]=mincx(lmisys,c, [0 0 0 0 0]);

X =dec2mat(lmisys,xopt,X);
W =dec2mat(lmisys,xopt,W);
r1 =dec2mat(lmisys,xopt,r1);
disp(copt);
disp(r1);
K =W *X^(-1);
disp('The best value:');
disp(sqrt(r1));
disp('Feedback gain K:');
disp(K/100);

%----------------------------------------solutions result--------------------
Solver for linear objective minimization under LMI constraints 

 Iterations   :    Best objective value so far 
 
     1
     2
     3
     4
     5
     6
     7
     8                 114.267501
     9                  59.802174
    10                  59.802174
    11                  41.613389
    12                  41.613389
    13                  41.613389
    14                  20.346897
    15                  20.346897
    16                  20.346897
    17                  10.262175
    18                  10.262175
    19                  10.262175
    20                   5.791484
    21                   5.791484
***                 new lower bound:    -1.071889
    22                   3.718387
***                 new lower bound:    -0.447187
    23                   3.718387
***                 new lower bound:    -0.074088
    24                   1.044904
***                 new lower bound:    -0.040169
    25                   1.000228
***                 new lower bound:     0.148979
    26                   0.960729
***                 new lower bound:     0.580998
    27                   0.862623
***                 new lower bound:     0.618936
    28                   0.862623
***                 new lower bound:     0.670347
    29                   0.798370
***                 new lower bound:     0.677624
    30                   0.790666
***                 new lower bound:     0.760378
    31                   0.784260
***                 new lower bound:     0.763410
    32                   0.781884
***                 new lower bound:     0.768376
    33                   0.780371
***                 new lower bound:     0.772957

 Result:  feasible solution of required accuracy
          best objective value:     0.780371
          guaranteed absolute accuracy:  7.41e-03
          f-radius saturation:  0.003% of R =  1.00e+09 
 
    0.7804

    0.7804

The best value:
    0.8834

Feedback gain K:
  112.1078   99.9032 -364.5474  -72.8227