前言

前面的基础算法笔记已经断更好久了，因为荔枝觉得还是得先学一下基础的数据结构知识之后才能更好的入门算法。在这篇文章中荔枝主要记录DFS和BFS的相关基础知识、答题的模板以及自己的一些浅薄理解，同样的也会涉及到相关的剪枝操作。

一、搜索算法概念

在大多数实际的问题求解过程中，其实很多的问题都会被转化为搜索问题，不论是最优路径的选取还是极值的获取其实都是在搜寻着最符合我们预期的答案。换一种理解的方式：其实搜索算法也是通过有目的的枚举来获取最优解的过程。搜索算法又可以分为盲目搜索和启发式搜索，我们首先来看看盲目搜索的两种方式：深度优先搜索和广度优先搜索。

二、深度优先搜索(DFS)

深度优先搜索就是按照树的深度沿着树的某一分支遍历树的结点直到抵达目的结点的过程，如果该分支无法抵达目的节点则会进行回溯到前面的结点并再次进行深度优先搜索直至找到目的结点。DFS一般使用递归的方式和栈这一数据结构，因此DFS如果不进行剪枝操作效率会比较低。在数据结构中，二叉树是一种使用DFS场景比较多的数据结构，换而言之，图论中的深度优先搜索其实就是二叉树的递归遍历过程，像二叉树最长路径、二叉树遍历、二叉树深度等等经典的题目往往都需要使用到深度优先搜索的方法。但也正如前面所说的那样，其实二叉树深度优先搜索算法的底层实现还是栈这一数据结构，这就要求我们在前面的使用的时候需要考虑到我们的程序执行会不会爆栈，这时候也就需要一定的操作或者技巧来简化深度优先搜索的过程。

荔枝在刷完leecode的DFS简单题目后直观感觉其实DFS用得好最主要的就是你的递归算法的基本功牢不牢，其实DFS也就是一种递归的体现，归结为其实任何算法题目都是“有迹可循”的，我们可以看看这几道题目来大致弄清楚深度优先搜索的打题模板，之后再面对DFS的题目能有一个大致的方向。

2.1 Leecode104——二叉树的最大深度

题目描述
给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
输入示例
[3,9,20,null,null,15,7]，
3
/ \
9 20
/ \
15 7
输出示例：
3

这道题目其实就是求二叉树一共有多少层，这个场景可以说其实就非常适合使用DFS来求解了，具体思路也很简单：从根节点沿着所有的路径走一遍并根据路径中的节点组成的层数来更新并返回最大深度。可以看到荔枝给了两种代码，很明显最下面的官方题解接很简洁明了哈哈哈，大家可以看出其实最基本的就是递归的运用。

demo示例：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
    //最大深度其实也是一种最长的路径
    //首先先确实边界条件
        if(root == nullptr){
            return 0;
        }
        if(root->left==nullptr && root->right==nullptr){
            return 1;
        }
        int depth = 0;
        if(root->left!=nullptr){
            depth=max(depth,maxDepth(root->left));
        }
        if(root->right!=nullptr){
            depth = max(depth,maxDepth(root->right));
        }
        return depth+1;
    }
};
// 另一种思路
// class Solution {
// public:
//     int maxDepth(TreeNode* root) {
//         if (root == nullptr) return 0;
//         return max(maxDepth(root->left), maxDepth(root->right)) + 1;
//     }
// };

来源：力扣（LeetCode）
链接： https://leetcode.cn/problems/maximum-depth-of-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2.2 Leecode257——二叉树的所有路径

题目描述：
给你一个二叉树的根节点 root ，按任意顺序，返回所有从根节点到叶子节点的路径。
叶子节点是指没有子节点的节点。

输入示例：
[1,2,3,null,5]
输出：
["1->2->5","1->3"]

这道题的解题思路跟上面的题目其实是一样的，对于一个节点，我们仅需要确定一条路径的终止记录的条件：就是遇到叶子节点，而对于一个根节点我们需要的是将左子树和右子树的路径记录下即可，我们无需太过纠结递归的过程实现，毕竟人脑压不了那么多栈哈哈哈哈哈。

demo示例：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void getPath(TreeNode* root,vector<string>& v,string s){
        if(root!=nullptr){
            s = s + "->" + to_string(root->val);
            if(root->left==nullptr && root->right==nullptr){
                v.push_back(s);
            }else{
                getPath(root->left,v,s);
                getPath(root->right,v,s);
            }
        }
        
    }
    
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> v;
        // 判断边界条件
        if(root == nullptr){
            return v;
        }else{
            if(root->left==nullptr && root->right==nullptr){
                v.push_back(to_string(root->val));
                return v;
            }
            getPath(root->left,v,to_string(root->val));
            getPath(root->right,v,to_string(root->val));
        }
        return v;
    }
   
};

来源：力扣（LeetCode）
链接： https://leetcode.cn/problems/binary-tree-paths/
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2.3 Leecode783——二叉搜索树节点的最小距离

题目描述：
给你一个二叉搜索树的根节点 root ，返回树中任意两不同节点值之间的最小差值。
差值是一个正数，其数值等于两值之差的绝对值。

输入示例：
[4,2,6,1,3]
输出示例：
1

demo示例：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int result=1000000;
    TreeNode* node = nullptr;
    int minDiffInBST(TreeNode* root) {
        dfs(root);
        return result; 
    }
    void dfs(TreeNode* root){
        if(root==nullptr) return;
        dfs(root->left);
        if(node!=nullptr){
            result=min(result,abs(root->val-node->val));
        }
        node = root;
        dfs(root->right);
    }
};

题目来源：力扣（LeetCode）
链接： https://leetcode.cn/problems/minimum-distance-between-bst-nodes/
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

我们已经上面三道简单题目，其实可以看到递归的影子无处不在，这也是荔枝的感受。也就是说我们再拿到一道DFS问题的时候需要直接反应出来找递归实现的条件，并抓住递归这一个方向来解决问题。对于DFS题目来说，更多的例题还是在考察二叉树的递归序列的应用，通过对前面二叉树题目的答题模板有了大致的了解，但是可能大多人会跟荔枝一样，对于这些概念都很清楚，但做起题目来还是一看就会，一写就废，我们应该如何去解题呢？首先还是需要弄清楚题目的意思，这是最重要的；其次我们需要对二叉树的递归顺序和二叉树的递归遍历了解清楚，知道什么时候适合用前序遍历、什么时候适合用后序遍历、什么时候使用中序遍历。具体举个例子：比如在Leecode.236二叉树的最近公共祖先这道题目中，我们需要从叶端往根端去处理，这时候就需要用到中序遍历来实现。因此什么题目适合什么方向来解题取决于你对二叉树知识的灵活运用，这很重要！

三、广度优先搜索(BFS)

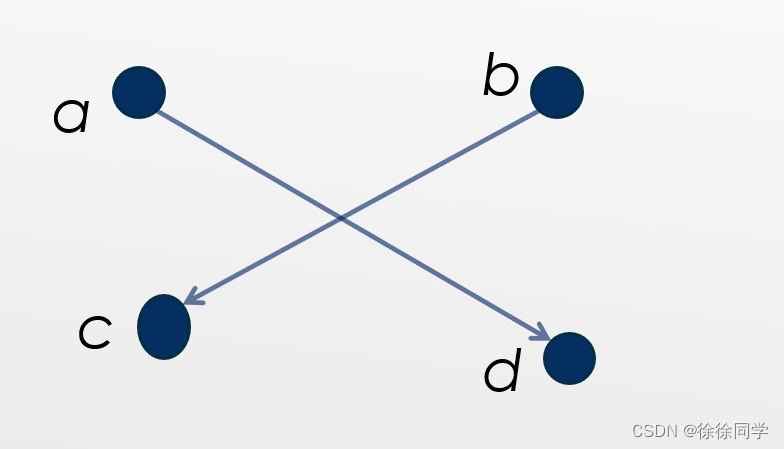
广度优先搜索与深度优先搜索相比最大的不同就是BFS更加侧重于状态的选取和标记。也就是说，BFS在遇到每一搜索层的时候就会标记所有的岔路并注意进入岔路并标记，通过反复的标记和回退，将通往目的结点的路径(最优解)记录下来。BFS使用到的数据结构是队列，它的复杂度跟深度优先搜索相同，本质上都是一种穷举的方法。其实简单的借助二叉树来理解广度优先搜索更好，因为二叉树的层序遍历其实就类似于图论中的广度优先搜索。我们先来看看这张图:

从上面的一个简单的二叉树中我们使用层序遍历遍历其节点：4-2-3-6-4-7-5，简单的说就是按层来遍历，类比于BFS来说我们是按层来搜索的，因此我们才称为广度优先搜索。那么如何使用广度优先搜索来解决题目，首先跟荔枝来看看这道例题：

3.1 Leecode102.——二叉树的层序遍历

题目描述：
给你二叉树的根节点 root ，返回其节点值的层序遍历（即逐层地，从左到右访问所有节点）。
输入：
root = [3,9,20,null,null,15,7] 输出：
[[3],[9,20],[15,7]]

demo示例：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> v;
        queue<TreeNode*> q;
        if(root!=nullptr) q.push(root);
        while(!q.empty()){
            int size = q.size();
            vector<int> vec;
            while(size--){
                TreeNode* front = q.front();
                vec.push_back(front->val);
                q.pop();
                if(front->left!=nullptr){
                    q.push(front->left);
                }
                if(front->right!=nullptr){
                    q.push(front->right);
                }
            }
            v.push_back(vec);
        }
        return v;
    }
};

这道题目就是一道非常经典的BFS题目了，首先我们借助了队列这一数据结构，可以看到这里用了两层while循环，外层的循环其实记录当前层级需要处理的节点数目，因为在开始对子节点进行处理的时候队列的大小会发生变化，所以需要提前记住当前层级的节点数目，内层循环则是对当前层级的二叉树节点进行分别进行出队操作和将其左右子节点压入队列中。需要注意的是我们需要一开始将根节点入队，才能顺利进入循环中，同时根节点入队操作的出发判别也作为了正确输入的边界条件。

来源：力扣（LeetCode）
链接： https://leetcode.cn/problems/binary-tree-level-order-traversal/
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

3.2 二叉树的最大深度问题

关于二叉树的最大深度问题我们已经在2.1中详细的介绍了，这道题目是Leecode的第104题，这里荔枝也就不再对问题的描述和输入输出的用例进行赘述了，我们现在尝试着使用BFS的模板来解题。

demo示例：

class Solution{
    public:
        int maxDepth(TreeNode* root){
            int depth = 0;
            queue<TreeNode*> q;
            if(root!=nullptr){
                q.push(root);
            }
            while(!q.empty()){
                int size = q.size();
                while(size--){
                    TreeNode* node = q.front();
                    q.pop();
                    if(node->left!=nullptr){
                        q.push(node->left);
                    }
                    if(node->right){
                        q.push(node->right);
                    }
                }
                depth++;
            }
            return depth;
        }
};

可以看出这里荔枝采用的是BFS的经典模板解法，在每层的队列循环结束之后都会让层数depth自增一，从而算出该二叉树的最大深度。

3.3 二叉树的最小深度

我们再来看看这道题目：

题目描述：
给定一个二叉树，找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明：叶子节点是指没有子节点的节点。

输入示例：
root = [3,9,20,null,null,15,7]

输出示例：
2

来源：力扣（LeetCode）
链接： https://leetcode.cn/problems/minimum-depth-of-binary-tree/
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

demo示例：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        if(root==nullptr){
            return 0;
        }
        queue<TreeNode*> q;
        int depth = 0;
        q.push(root);
        while(!q.empty()){
            int size = q.size();
            depth++;
            while(size--){
                TreeNode* node = q.front();
                q.pop();
                if(node->left){
                    q.push(node->left);
                }
                if(node->right){
                    q.push(node->right);
                }
                if(node->left==nullptr && node->right==nullptr){
                    return depth;
                }
            }
            
        }
        return depth;
    }
};

四、剪枝操作

4.1 可行性剪枝

可行性剪枝其实就是根据题目的要求对DFS或者是BFS所枚举出的所有搜索可能进行裁剪，如果对于其中的一种状态情况可以推出按照这个方向之后的所有的情况都与题目的要求不符，那么就对当前的所有情况和之后的所有情况进行判负，直接放回当前的状态结果。

4.2 最优性剪枝

在求解最优化的问题时，往往可能应为暴力枚举或者是盲目搜索而导致程序超时，这时候我们需要借助于我们已有的最优解，对于搜索得到的结果比最优结果差，那我们就无需再往这个方向搜索，直接返回程序的状态即可。

4.3 重复性剪枝

重复性剪枝其实就是排除等效冗余的过程，对于可能出现的重复出现最优解的请况仅需选取一种即可。

4.4 奇偶性剪枝

奇偶性剪枝更多的应用在迷宫问题中，我们往往借助奇数和偶数的特性对路径结果搜索进行简化。我们来看看一个迷宫问题：

有一个n*m的迷宫，一个探险者每个单位时间只能上下左右移动一格，现在规定T时间目的地大门打开，问探险者能逃离迷宫吗？注意不能走回头路，也不能碰到障碍物。在解题时我们可以将将n * m的网格染成黑白色，相邻的两个格子的颜色不一样。我们记每个格子的行数和列数之和为x，如果x为偶数，那么格子就是白色，反之奇数时为黑色。我们可以得出这样一个结论：走奇数会改变颜色，走偶数步则颜色不变。如果起点和终点的颜色一样，而T是奇数的话，就不可能离开迷宫。

借助这个处理过程我们可以根据具体题目的要求将路径的搜索范围进行缩小。