python 基础系列篇:八、熟练掌握推导式
- 推导式
- 特殊的元组推导式
- 推导式机制
- 玩转推导式
- 小结
推导式
在python提供的各种语法糖中,老顾最青睐的就是这个推导式,他大大减少了代码的书写量。
比如一个正常的,生成长度为5的列表,其内容为连续自然数1到5,用正常的循环方式,书写就很长。
arr = []
for i in range(5):
arr.append(i + 1)
而使用推导式,则就很简短
arr = [i + 1 for i in range(5)]
在 python 中,可以用推导式方式生成很多内容,比如 字典、列表、集合、元组。
# 列表推导式
[n for n in range(100)]
# 集合推导式
{n for n in range(100)}
# 字典推导式
{n:n for n in range(100)}
# 元组推导式
(n for n in range(100))
CSDN 文盲老顾的博客,https://blog.csdn.net/superwfei
特殊的元组推导式
在其他推导式方式中,每次都是得到对应类型的数据,即:推导即结果。
而在元组推导式方式中,比较特殊,他得到的并不是一个元组结果,而是一个生成式类型的结果。

只有在第一次使用的时候,他才会转成元组数据,但是,这个推导式是不可复用的,需要自行注意。
推导式机制
1、只能使用迭代
在推导式中,我们只能使用迭代方式进行推导,也就是说,只能使用 for。因为迭代对象是有限的,所以,得到的长度在推导式运行之前就已经确定了,内容也确定了,只是省略了我们的复制步骤。
2、不能引用自身数据
同样,我们无法在推导式内引用之前步骤生成的数据,比如我们想直接用推导式生成一个斐波那契数列,那是不可以的(使用公式进行计算的除外)。
3、可以使用三元表达式
[n + 1 if n % 2 == 1 else n // 2 for n in range(10)]
Out[6]: [0, 2, 1, 4, 2, 6, 3, 8, 4, 10]
[n + 1 if n % 2 == 1 else n // 2 + 1 for n in range(10)]
Out[7]: [1, 2, 2, 4, 3, 6, 4, 8, 5, 10]

在 for 之前的 if else 即为三元运算。这个方式是无论条件是否满足,都会有数据生成在推导式结果内。
本例推导式等价于
def tempFun():
arr = []
for n in range(10):
if n % 2 == 1:
arr.append(n + 1)
else:
arr.append(n // 2 + 1)
return arr
4、筛选表达式
[n for n in range(40) if n % 3 == 0 and n > 0]
Out[8]: [3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39]

在迭代表达式之后的 if ,即为筛选表达式,只有满足条件的内容,才会生成在推导式结果内,如果不满足,则不会在推导式结果中体现。
本例推导式等价于
def tempFun():
arr = []
for n in range(40):
if n % 3 == 0 and n > 0:
arr.append(n)
return arr
5、多重迭代推导式
这里所说的多重迭代推导式,是并列的多个 for 迭代,而不是嵌套迭代哦。
# 嵌套迭代推导式
[[n + m * 5 for n in range(5)] for m in range(5)]
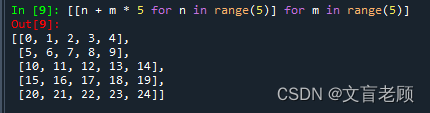
# 多重迭代推导式
[n for n in range(5) for m in range(5)]

根据结果,我们可以得出一个结论,那就是:多重迭代推导式,顺序是从左向右的。
先迭代一次 n,得到 n=0,然后迭代5次m,结果生成5个0,然后再迭代一次n,得到n=1,然后迭代5次m,结果生成5个1。。。。直到最左边的迭代结束,我们可以用下边这个推导式再次验证一下。
[[x,y,z] for x in range(3) for y in range(3) for z in range(3)]
Out[11]:
[[0, 0, 0],
[0, 0, 1],
[0, 0, 2],
[0, 1, 0],
[0, 1, 1],
[0, 1, 2],
[0, 2, 0],
[0, 2, 1],
[0, 2, 2],
[1, 0, 0],
[1, 0, 1],
[1, 0, 2],
[1, 1, 0],
[1, 1, 1],
[1, 1, 2],
[1, 2, 0],
[1, 2, 1],
[1, 2, 2],
[2, 0, 0],
[2, 0, 1],
[2, 0, 2],
[2, 1, 0],
[2, 1, 1],
[2, 1, 2],
[2, 2, 0],
[2, 2, 1],
[2, 2, 2]]
本例推导式等价于
def tempFun():
arr = []
for x in range(3):
for y in range(3):
for z in range(3):
arr.append([x,y,z])
return arr
6、多重迭代筛选推导式
[[x,y,z] for x in range(10) if x % 2 == 0 for y in range(10) if y % 3 == 0 for z in range(10) if z % 5 == 0]
Out[15]:
[[0, 0, 0],
[0, 0, 5],
[0, 3, 0],
[0, 3, 5],
[0, 6, 0],
[0, 6, 5],
[0, 9, 0],
[0, 9, 5],
[2, 0, 0],
[2, 0, 5],
[2, 3, 0],
[2, 3, 5],
[2, 6, 0],
[2, 6, 5],
[2, 9, 0],
[2, 9, 5],
[4, 0, 0],
[4, 0, 5],
[4, 3, 0],
[4, 3, 5],
[4, 6, 0],
[4, 6, 5],
[4, 9, 0],
[4, 9, 5],
[6, 0, 0],
[6, 0, 5],
[6, 3, 0],
[6, 3, 5],
[6, 6, 0],
[6, 6, 5],
[6, 9, 0],
[6, 9, 5],
[8, 0, 0],
[8, 0, 5],
[8, 3, 0],
[8, 3, 5],
[8, 6, 0],
[8, 6, 5],
[8, 9, 0],
[8, 9, 5]]
在每一个迭代后边,都可以跟上一个筛选表达式,这是合法的。
本例推导式等价于
def tempFun():
arr = []
for x in range(10):
if x % 2 == 0:
for y in range(10):
if y % 3 == 0:
for z in range(10):
if z % 5 == 0:
arr.append([x,y,z])
return arr
玩转推导式
推导式本身,并不限定嵌套的推导式层数,根据这个,我们可以试着写一个素数判断,比如来个1000以内的所有素数。
[n for n in range(2,1000) if len([x for x in range(2,n) if n % x == 0]) == 0]
在比如,要求每行5个输出素数
print(''.join([v + ' ' if i % 5 != 4 else v + '\n' for i,v in enumerate([str(n) for n in range(2,1000) if len([x for x in range(2,n) if n % x == 0]) == 0])]))
更比如,输出所有三位数的素数,且这个素数的每一位也都是素数
print(''.join([v + ' ' if i % 5 != 4 else v + '\n' for i,v in enumerate([str(n) for n in range(100,1000) if len([x for x in range(2,n) if n % x == 0]) == 0 and len(set(str(n)) - set('2357')) == 0])]))
比如统计一段文本中,每个字符出现的次数
a = 'aw;oei ja;ofnme; aoiwejf;aoiewj;lz uj;orijdfsoerijhg;osef'
print({c:a.count(c) for c in set(a)})
{'l': 1, 'e': 6, 'h': 1, 'n': 1, 'd': 1, ';': 7, 'w': 3, 'o': 7, 's': 2, 'z': 1, 'j': 6, ' ': 3, 'a': 4, 'r': 2, 'f': 4, 'g': 1, 'm': 1, 'u': 1, 'i': 5}
再比如,降序输出每个字符出现的次数
a = 'aw;oei ja;ofnme; aoiwejf;aoiewj;lz uj;orijdfsoerijhg;osef'
print({c:a.count(c) for c in sorted({c for c in set(a)},key = lambda x:(-a.count(x),x))})
{';': 7, 'o': 7, 'e': 6, 'j': 6, 'i': 5, 'a': 4, 'f': 4, ' ': 3, 'w': 3, 'r': 2, 's': 2, 'd': 1, 'g': 1, 'h': 1, 'l': 1, 'm': 1, 'n': 1, 'u': 1, 'z': 1}
小结
经过本文的一些示例,相信小伙伴们也对这个推导式有了进一步的认知了。由于推导式的嵌套方式比较方便,比我们单独写循环要便捷很多很多,所以在一些确定计算方式的内容,老顾都会用推导式来进行数据整理,有兴趣的可以到老顾的社区,看看每日一练的做法,大部分都是由推导式进行完成的。
对于推导式来说,关键是可迭代的对象作为初始数据来源,range 是最常用的,其次是 enumerate,再然后就是各个已存在的列表、字典、元组、集合或其他可迭代对象,比如正则迭代之类的。
在这里再向大家推荐一个迭代工具包,itertools,非常好用哦,它内置了一些方法,方便的生成一些可迭代对象。
总之呢,学会用好退到时候,是懒人的一大福音哦。