欢迎回到：遇见蓝桥遇见你，不负代码不负卿！

引入：二分查找

题目描述

题解

代码执行

复杂度分析

例题一：搜索插入位置

题目描述

题解

代码执行

复杂度分析

例题二：寻找峰值

题目描述

题解

代码执行

复杂度分析

例题三：搜索二维矩阵

题目描述

题解

代码执行

思考题

最大子序和

题目描述

代码执行

蓝桥结语：遇见蓝桥遇见你，不负代码不负卿！

好久不见啦铁汁们，蓝桥杯更新咯，快来尝尝鲜叭。

【前言】：由于本章基础知识点不多，所以笔者直接讲解四道典型题让大家感受一下二分法的美妙。

准备开始咯，坐稳哈...

引入：二分查找

【敲黑板】：用二分算法解题的前提是该数组有序！！！

【注意】：查找一次砍掉一半，效率非常高！但是条件比较苛刻，一定要有序！

题目描述

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例1：

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例2：

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

题解

设定左右指针
找出中间位置，并判断该位置值是否等于 target
nums[mid] == target 则返回该位置下标
nums[mid] > target 则右侧指针移到中间
nums[mid] < target 则左侧指针移到中间

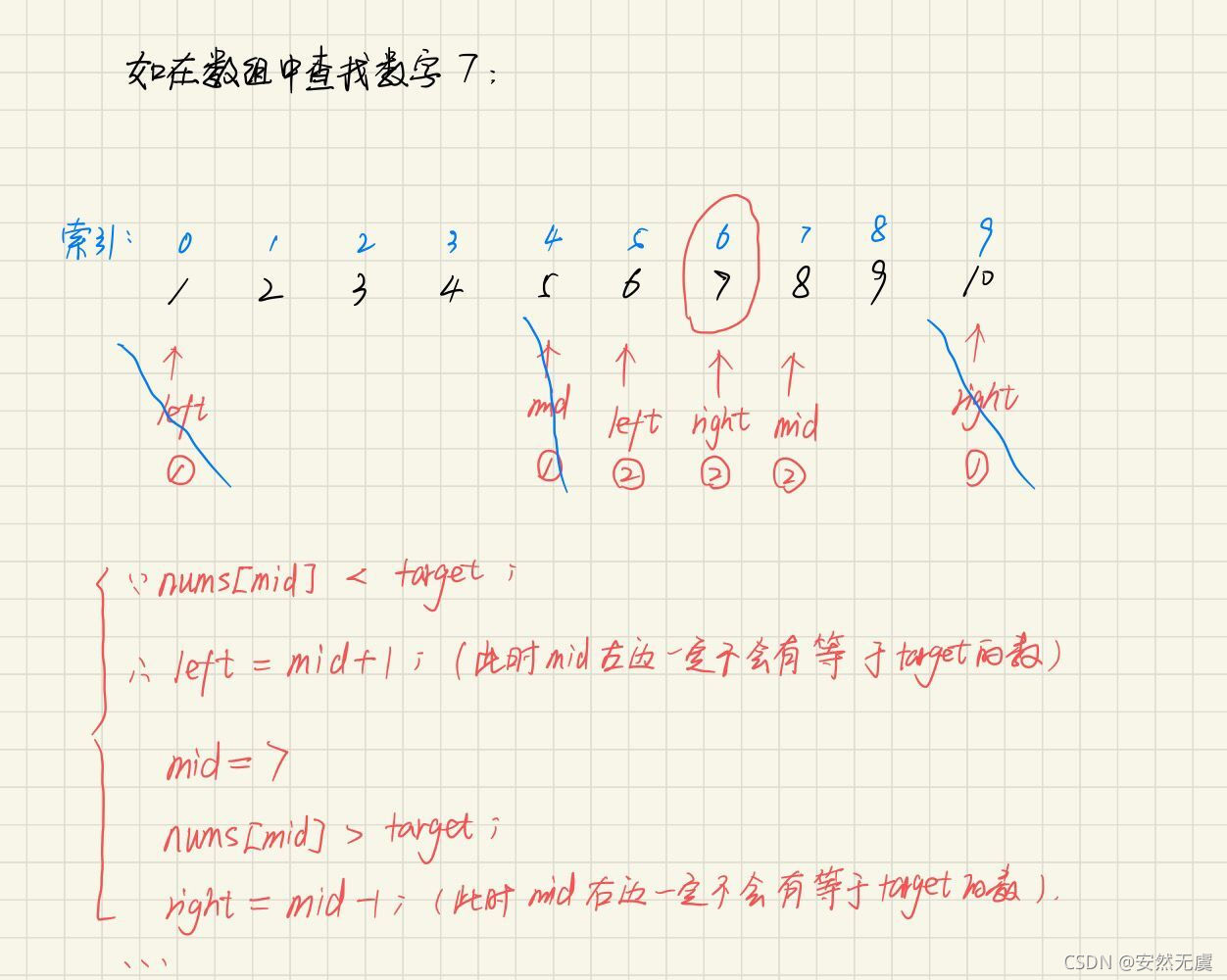
二分是一个比较简单的算法，只要大家记住上面这种套路就行啦。

代码执行

int search(int* nums, int numsSize, int target){
    //考虑特殊情况
    if(nums == NULL || numsSize == 0){
        return -1;
    }
    int left = 0;//起始元素的索引
    int right = numsSize - 1;//末尾元素的索引
    int mid = 0;
    while(left <= right){
        //应该有很多人会写成mid = (left + right) / 2;这种写法不谨慎
        //因为做的是加法运算，所以要考虑溢出的特殊情况
        mid = left + (right - left) / 2;
        if(nums[mid] < target){
            left = mid + 1;
        }else if(nums[mid] > target){
            right = mid - 1;
        }else{
            return mid;
        }
    }
    return -1;
}

【注意】：while判断表达式中是left <= right, 为什么还要加上left == right 的情况呢，当二者相等的时候说明还有一个元素需要被比较，所以当left > right时停下来，因为此时中间已经没有元素需要被比较了。至于为什么将mid = left + (right - left) / 2; 的形式，上面代码中已经讲咯。

复杂度分析

时间复杂度：O(logN)

空间复杂度：O(1)

看，二分法是很高效的，大家在今后的训练中，如果遇到查找搜索类的题目要求时间复杂度是O(logN)的，要想到二分法哦。

好嘞，这就是二分查找，是不是很简单，下面再补充几道典型例题，让大家熟悉二分。

例题一：搜索插入位置

题目描述

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

题目中要求使用时间复杂度为O(logN)的算法解题，所以结合本题题意，很容易就想到了二分法。

示例1：

输入: nums = [1,3,5,6], target = 5
输出: 2

示例2：

输入: nums = [1,3,5,6], target = 7
输出: 4

题解

整体思路和普通的二分查找几乎没有区别，先设定左侧下标 left 和右侧下标 right，再计算中间下标 mid
每次根据 nums[mid] 和 target 之间的大小进行判断，相等则直接返回下标，nums[mid] < target 则 left 右移，nums[mid] > target 则 right 左移
查找结束如果没有相等值则返回 left，该值为插入位置,注意哦，最后如果没有相等值，返回的是left

【注意】：

二分查找的思路不难理解，但是边界条件容易出错，比如循环结束条件中 left 和 right 的关系，更新 left 和 right 位置时要不要加 1 减 1。这些都是大家自己动手画图理解，用代码去体会，只可意会不可言传哦。

代码执行

int searchInsert(int* nums, int numsSize, int target){
    //考虑特殊情况
    if(nums == NULL || numsSize == 0){
        return -1;
    }
    int left = 0;
    int right = numsSize - 1;
    int mid = 0;
    while(left <= right){
        mid = left + (right - left) / 2;
        if(nums[mid] > target){
            right = mid - 1;
        }else if(nums[mid] < target){
            left = mid + 1;
        }else{
            return mid;
        }
    }
    return left;
}

复杂度分析

时间复杂度：O(logN)

空间复杂度：O(1)

是不是很简单，下面开始蹭加点难度咯，有点绕，需要仔细想哦，加油加油。

例题二：寻找峰值

题目描述

峰值元素是指其值严格大于左右相邻值的元素。

给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回任何一个峰值所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞ 。

你必须实现时间复杂度为 O(log n) 的算法来解决此问题。

示例1：

输入：nums = [1,2,3,1]
输出：2
解释：3 是峰值元素，你的函数应该返回其索引 2。

示例2：

输入：nums = [1,2,1,3,5,6,4]
输出：1 或 5 
解释：你的函数可以返回索引 1，其峰值元素为 2；
     或者返回索引 5， 其峰值元素为 6。

题解

【注意】：二分法解题的前提要求是有序的，这题看起来没说有序呀，那怎么还能用二分法呢，我们也不能先进行排序，因为会把索引打乱，那该怎么办呢，请朝后看...

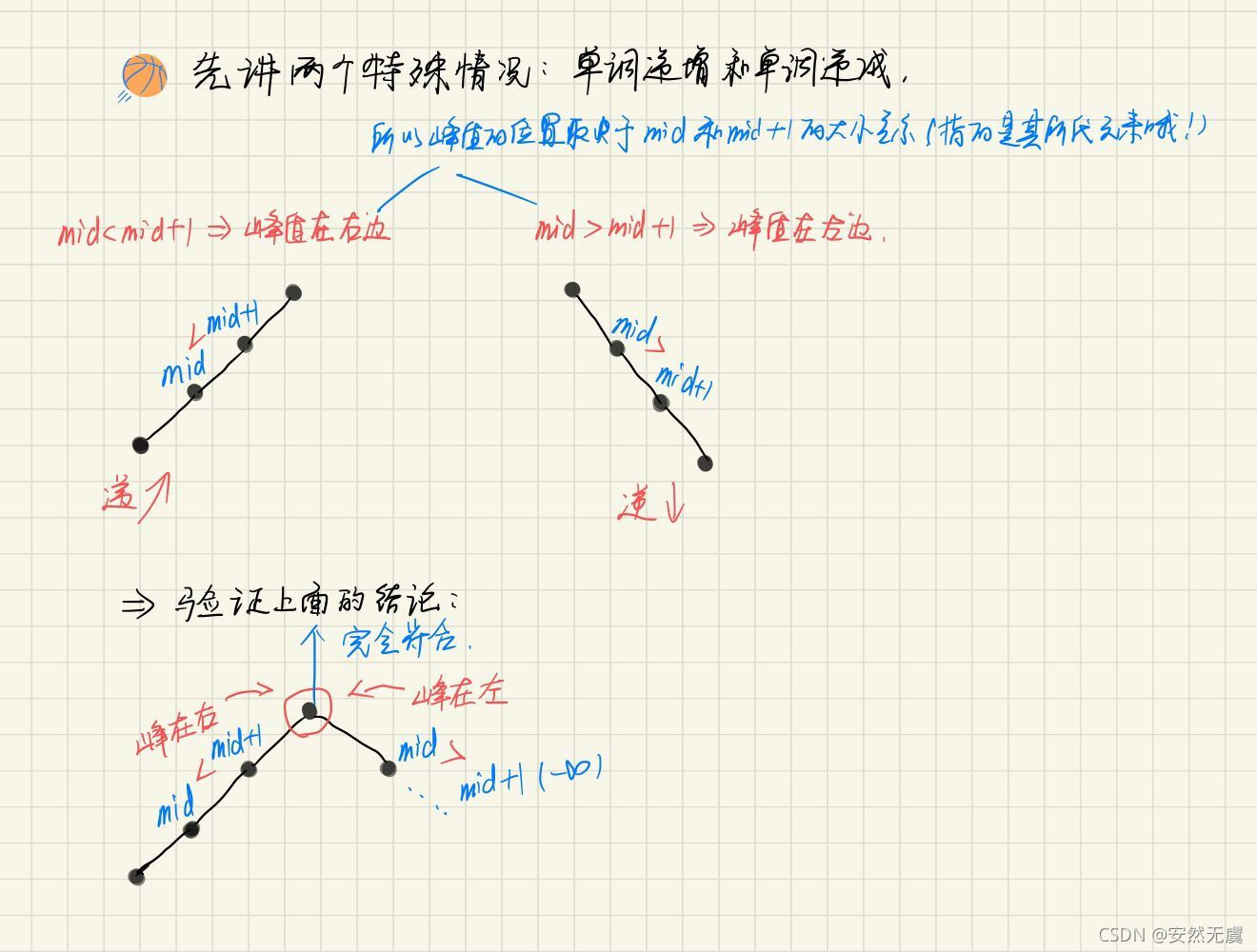
描述这个规律就是：

规律一：如果nums[mid] > nums[mid+1]，则在mid之前一定存在峰值元素
规律二：如果nums[mid] < nums[mid+1]，则在mid+1之后一定存在峰值元素

代码执行

int findPeakElement(int* nums, int numsSize){
    //考虑特殊情况
    if(nums == NULL || numsSize == 0){
        return -1;
    }
    int left = 0;
    int right = numsSize - 1;
    int mid = 0;
    while(left <= right){
        if(left == right){
            return left;
        }
        mid = left + (right - left) / 2;
        if(nums[mid] > nums[mid + 1]){
            right = mid;//mid之前一定存在峰值元素
        }else{
            left = mid + 1;//mid+1之后一定存在峰值元素
        }
    }
    return left;
}

复杂度分析

时间复杂度：O(logN)

空间复杂度：O(1)

例题三：搜索二维矩阵

题目描述

编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。

也就是说，整个二维数组都是升序的。

示例1：

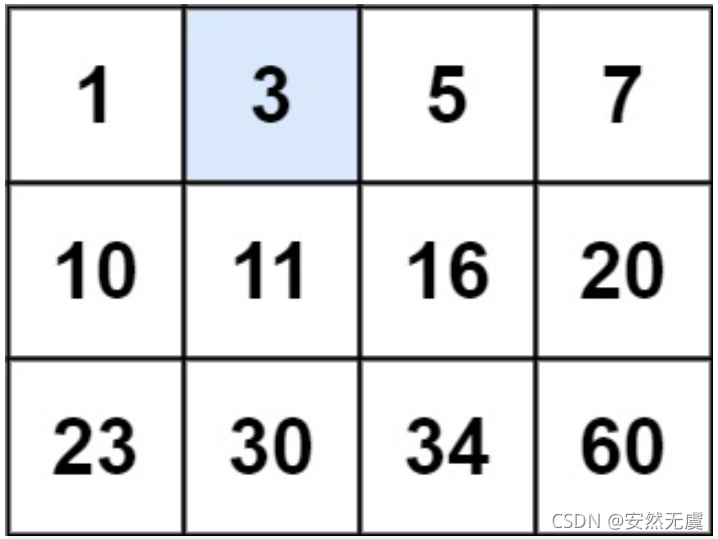
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例2：

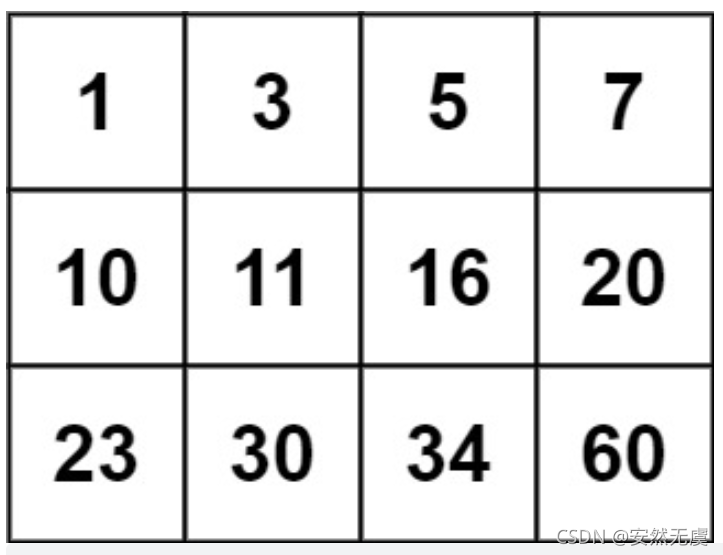
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

题解

【注意】：本题的重点就在于一维索引和二维索引间的互换

代码执行

bool searchMatrix(int** matrix, int matrixSize, int* matrixColSize, int target){
    //考虑特殊情况
    if(matrix == NULL || matrixSize == 0){
        return false;
    }
    int row = matrixSize;//行数
    int col = *matrixColSize;//列数
    int left = 0;//起始元素的索引
    int right = row * col - 1;//最后一个元素的索引
    int mid = 0;
    int element = 0;
    while(left <= right){
        mid = left + (right - left) / 2;
        element = matrix[mid / col][mid % col];//将一维的索引化成二维的索引
        if(element == target){
            return true;
        }else if(element > target){
            right = mid - 1;
        }else{
            left = mid + 1;
        }
    }
    return false;
}

复杂度分析

时间复杂度：O(logM*N), M,N分别是矩阵的行数和列数

空间复杂度：O(1)

好喽，铁汁把上面四道题目练习一遍，肯定就能对二分算法有一定的认识，加油加油哦。

思考题

大家先将上篇博文（分治算法）看一下，现在讲解那道留下的思考题。

蓝桥杯算法竞赛系列第三章——细谈递归的bro分治_安然无虞的博客-CSDN博客

最大子序和

题目描述

给定一个整数数组，找到一个具有最大和的连续子数组（子数组中至少包含一个数），要求返回其最大和。

注意：本题要求的是连续的子数组，可能有的题目要求可以是断开的，但本题不是。

将数组nums由中点mid分为三种情况：

1. 最大子串在左边

2. 最大子串在右边

3. 最大子串跨中点，左右两边元素都有（理解上的难点）

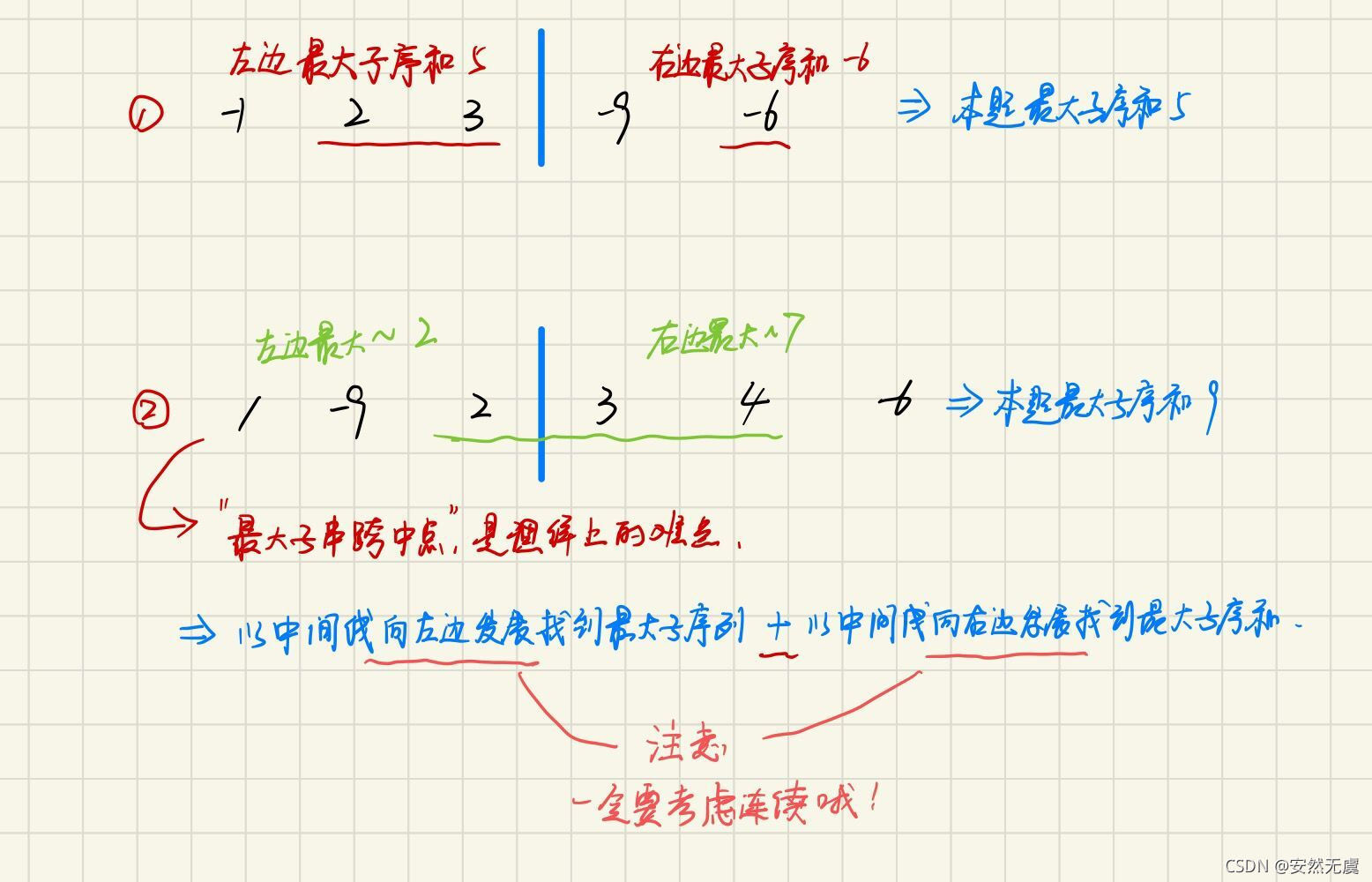
lSum 表示 [l,r] 内以 l 为左端点的最大子段和
rSum 表示 [l,r] 内以 r 为右端点的最大子段和
mSum 表示 [l,r] 内的最大子段和
iSum 表示 [l,r] 的区间和

代码执行

struct Status {
    int lSum, rSum, mSum, iSum;
};

struct Status pushUp(struct Status l, struct Status r) {
    int iSum = l.iSum + r.iSum;
    int lSum = fmax(l.lSum, l.iSum + r.lSum);
    int rSum = fmax(r.rSum, r.iSum + l.rSum);
    int mSum = fmax(fmax(l.mSum, r.mSum), l.rSum + r.lSum);
    return (struct Status){lSum, rSum, mSum, iSum};
};

struct Status get(int* a, int l, int r) {
    if (l == r) {
        return (struct Status){a[l], a[l], a[l], a[l]};
    }
    int m = l + (r - l) / 2;
    struct Status lSub = get(a, l, m);
    struct Status rSub = get(a, m + 1, r);
    return pushUp(lSub, rSub);
}

int maxSubArray(int* nums, int numsSize) {
    return get(nums, 0, numsSize - 1).mSum;
}

由于想让大家搞懂知识点，所以这里的题目可能用这种解法不是最优解，没关系，我会在后面的算法中补充到，在每日一题中也会涉及到。今天就不布置思考题咯，铁汁们好好把上面题目自己尝试做出来。