目录
优先队列
若采用数组或链表实现优先队列
数组
链表
有序数组
有序链表
总结
若采用二叉搜索树来实现优先队列
最大堆
堆的概念
优先队列的完全二叉树表示
堆的两个特性
结构性
有序性
【例】最大堆和最小堆
【例】不是堆
堆的抽象数据类型描述
优先队列
优先队列(Priority Queue):
特殊的“队列”,取出元素的顺序是依照元素的优先权(关键字)大小,而不是元素进入队列的先后顺序。
若采用数组或链表实现优先队列
数组
插入操作——元素总是插入尾部 ~
删除操作——查找最大(或最小) 关键字 ~
从数组中删去需要移动的元素 ~
插入操作的时间复杂度为O(1),只需要将元素插入到数组的末尾即可。
但是删除操作的时间复杂度为O(n),因为需要找到优先级最高的元素,这可能需要遍历整个数组。
链表
插入操作——元素总是插入链表的头部 ~
删除操作——查找最大(或最小)关键字 ~
删去结点 ~
插入操作的时间复杂度为O(1),同样只需要在链表末尾插入一个节点即可。
而删除操作时,查找最大(或最小)关键字可能需要遍历整个链表再进行删除,所以时间复杂度为O(n)。
有序数组
插入操作——找到合适的位置 ~ 或
移动元素并插入 ~
删除操作——删去最后一个元素 ~
采用有序数组使得优先队列在删除时方便了很多,但是在插入时却同样会变得十分麻烦,要找到合适的位置进行插入,再移动元素。
有序链表
插入操作——找到合适的位置 ~
插入元素 ~
删除操作——删除首元素或最后元素 ~
除了在插入时不用移动元素,有序链表与有序数组基本相同。
总结
给出的这四个方案中,总有存在不足。要么是提高了插入操作的效率,删除操作的效率十分低;要么是提高了删除操作的效率,而插入操作的效率十分低。
所以我们要想用一种新的方式来存储:二叉树
若采用二叉搜索树来实现优先队列
通过前面的学习,我们了解到:
在二叉搜索树中,每个结点都有一个键值,且左子树中的所有结点的键值小于该结点的键值,右子树中的所有结点的键值大于该结点的键值。
因此,可以将优先级作为键值,将元素作为结点存储在二叉搜索树中。
在插入元素时,根据元素的优先级将其插入到正确的位置。
在删除元素时,可以删除具有最高优先级的元素,即最大元素或最小元素。
但是,
当我们连续删除最大值或者连续删除最小值时,这棵二叉搜索树会变得越来越斜,二叉搜索树的插入和删除操作的时间复杂度可能会退化为O(n)。达不到我们要求的高效率了。
所以,我们要思考:采用二叉树的结构来实现这个优先队列的话,要更应该关注插入操作还是删除操作?
最大堆
很显然,采用二叉树结构来实现优先队列时,更应该关注的是删除操作,连续不断地删除二叉搜索树的最值的话,会使得其越来越不平衡。
那么就不删除左右子树,改为删除根结点。
我们把最大值放在根结点上,要删除最大值时直接删除根结点即可。
故而有一个原则:任何一个结点,都是以它为根的这个子树的最大值。
那么满足这个原则的结构,我们称它为最大堆。
为了是这个二叉树能够平衡一点,我们在实现时,最好的方法应该是使用完全二叉树。
我们引出堆的概念:
堆的概念
堆是一种特殊的树形结构,其中每个结点都有一个值,通常称为“键值”,并且每个结点的键值都满足一定的条件。
其中具有最高(或最低)优先级的元素总是位于堆的根结点。
堆可以分为最大堆和最小堆,
最大堆中父结点的键值总是大于或等于任何一个子结点的键值,
而最小堆中父结点的键值总是小于或等于任何一个子结点的键值。
而堆的一个特点就是用完全二叉树来存储。
优先队列的完全二叉树表示

堆的两个特性
结构性
用数组表示的完全二叉树。
有序性
任一结点的关键字是其子树所有结点的最大值(或最小值)
- “最大堆(MaxHeap)”,也称“大顶堆”:最大值
- “最小堆(MinHeap)”,也称“小顶堆”:最小值
【例】最大堆和最小堆
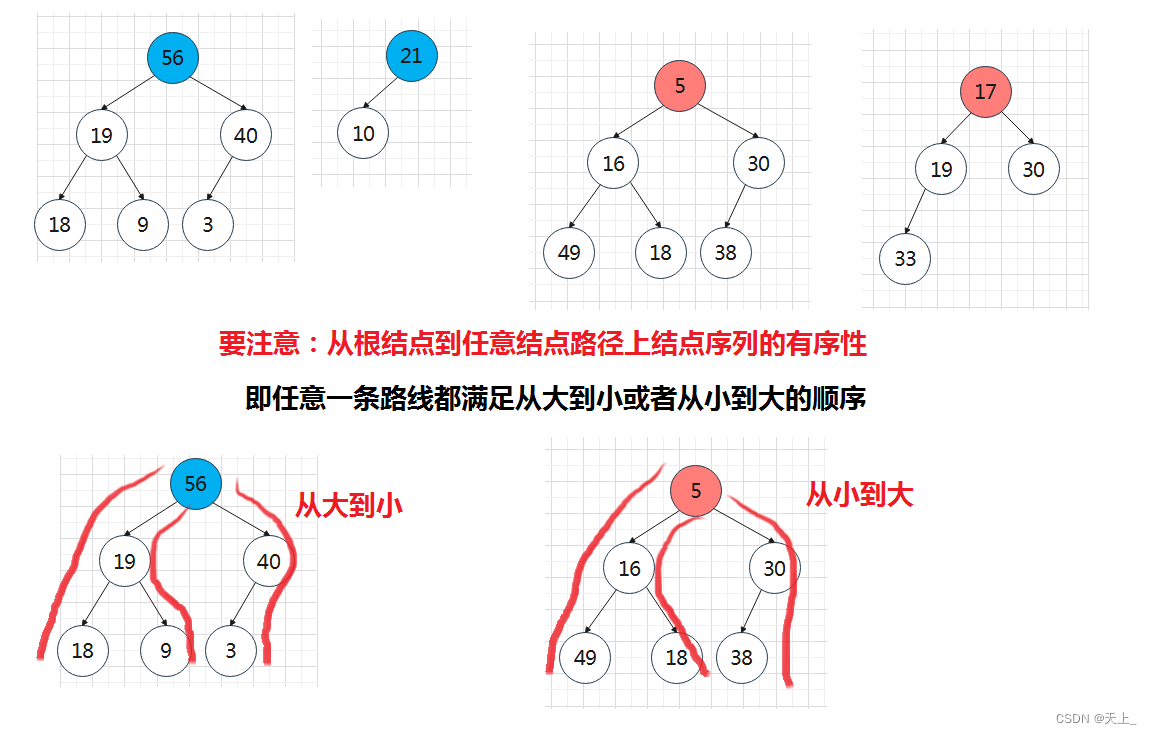
【例】不是堆

堆的抽象数据类型描述
类型名称:最大堆(MaxHeap)
数据对象集:完全二叉树,每个结点的元素值不小于其自子结点的元素值
操作集:最大堆HMaxHeap,元素item
ElementType,主要操作有:
- MaxHeap Create(int MaxSize):创建一个空的最大堆。
- Boolean IsFull(MaxHeap H):判断最大堆H是否已满。
- Insert(MaxHeap H,ElementType item):将元素item插入最大堆H。
- Boolean IsEmpty(MaxHeap H):判断最大堆H是否为空。
- ElementType DeleteMax(MaxHeap H):返回H中最大元素(高优先级)。
end
学习自:MOOC数据结构——陈越、何钦铭