这里写自定义目录标题
- 仿真绘图内容
- 发动机最优曲线
- 最优燃油消耗率曲线
- 最优效率曲线
- 工作时间/能量消耗的分布
- 传统车动力性分析
- 绘制三(或多个)y坐标轴函数
- 统计数据分布情况函数
仿真绘图内容
从传统车到新能源混合动力车型的不同绘制。
发动机最优曲线
发动机最优曲线最常见为最优燃油消耗率曲线,即同一机械输出功率下,燃油消耗率最小的转速转矩对应的发动机工作点。
最优燃油消耗率曲线
最优效率曲线
工作时间/能量消耗的分布
包括转速-转矩工作点的时间统计分布,能够反映出发动机工作点(转速-转矩)的工作点时间的花费情况。
以及转速-转矩工作点的能量统计分布,能够反映出发动机工作点(转速-转矩)的工作点能量(或者油耗)的花费情况。
传统车动力性分析
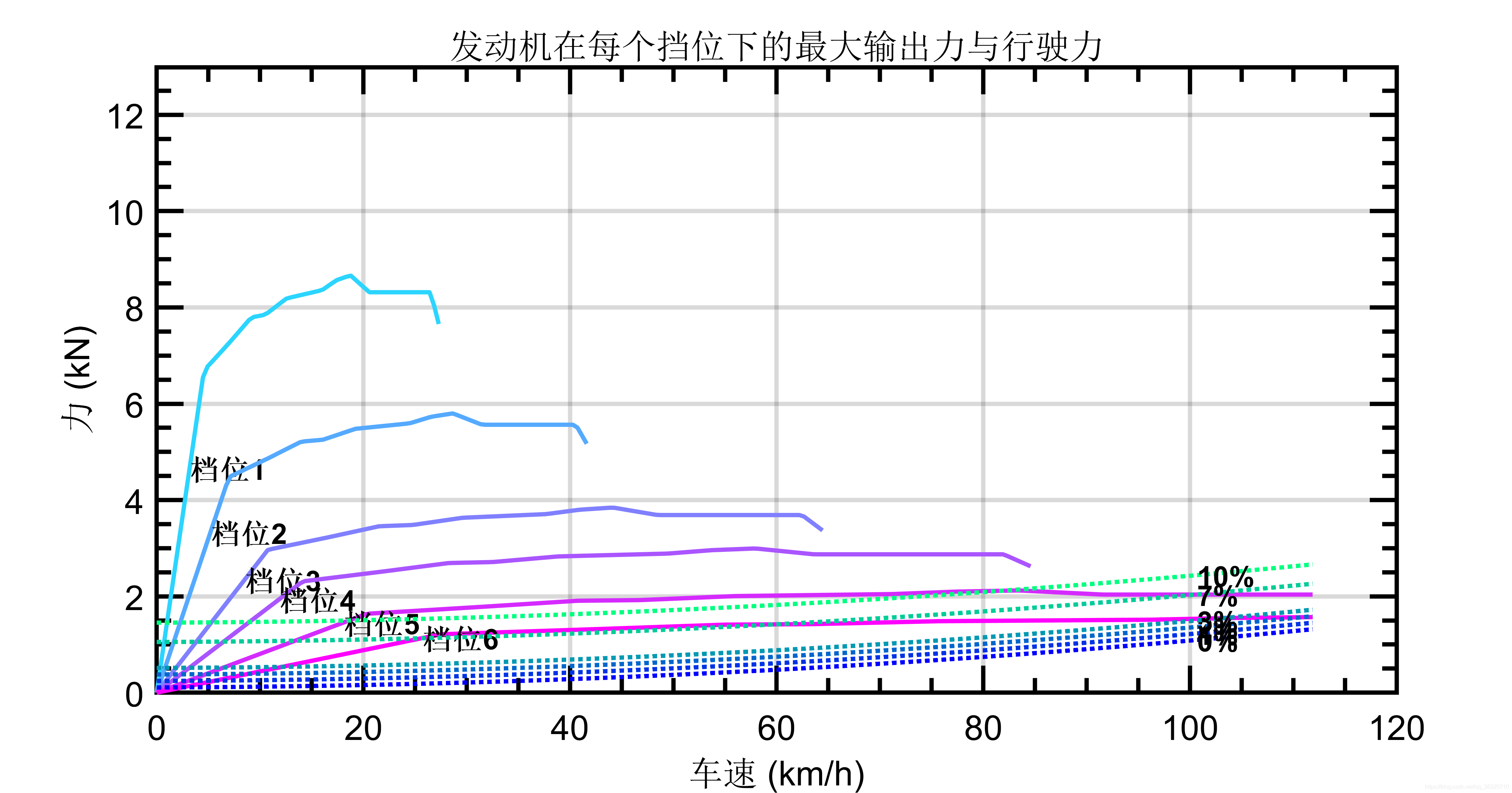
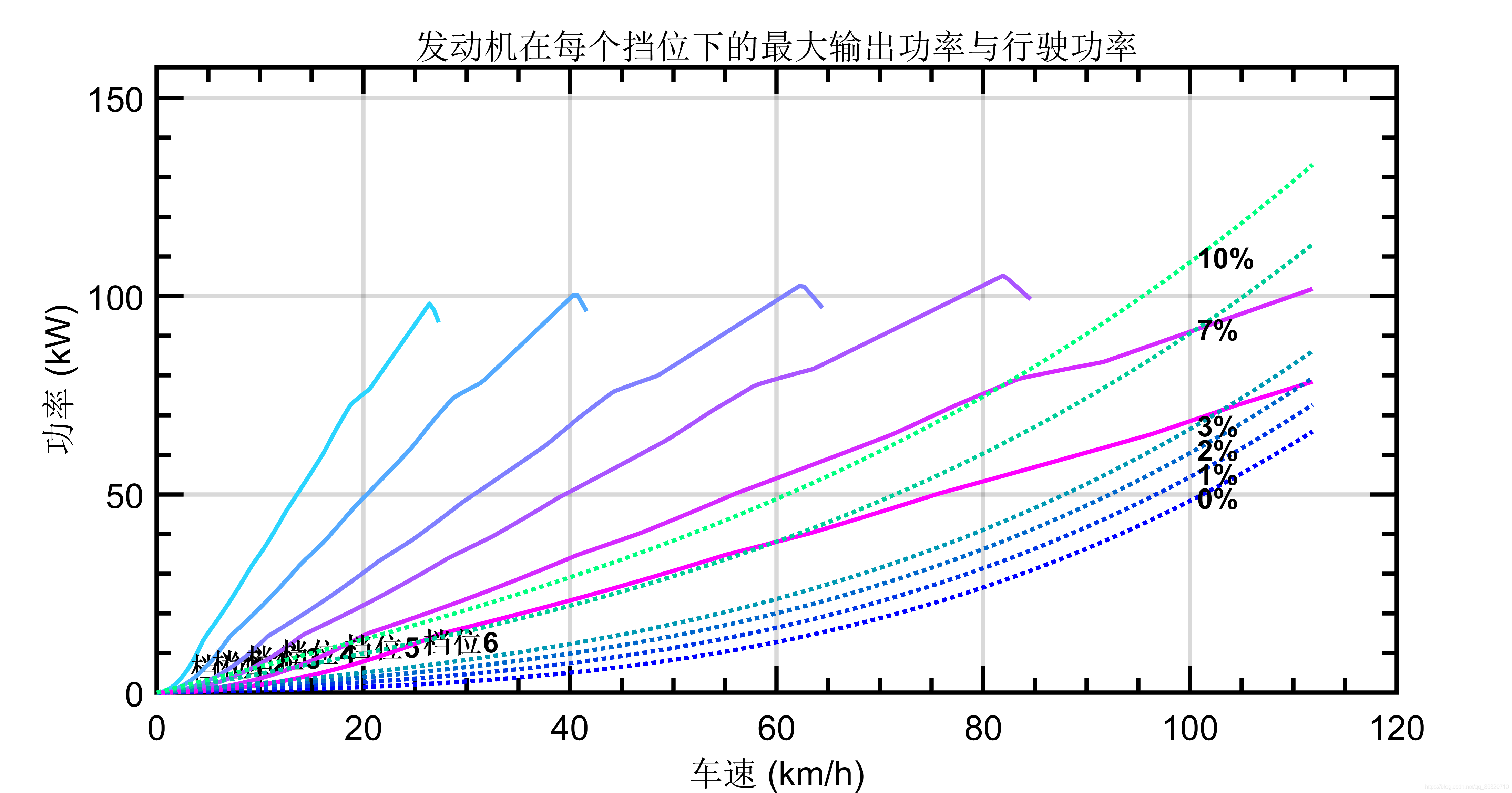
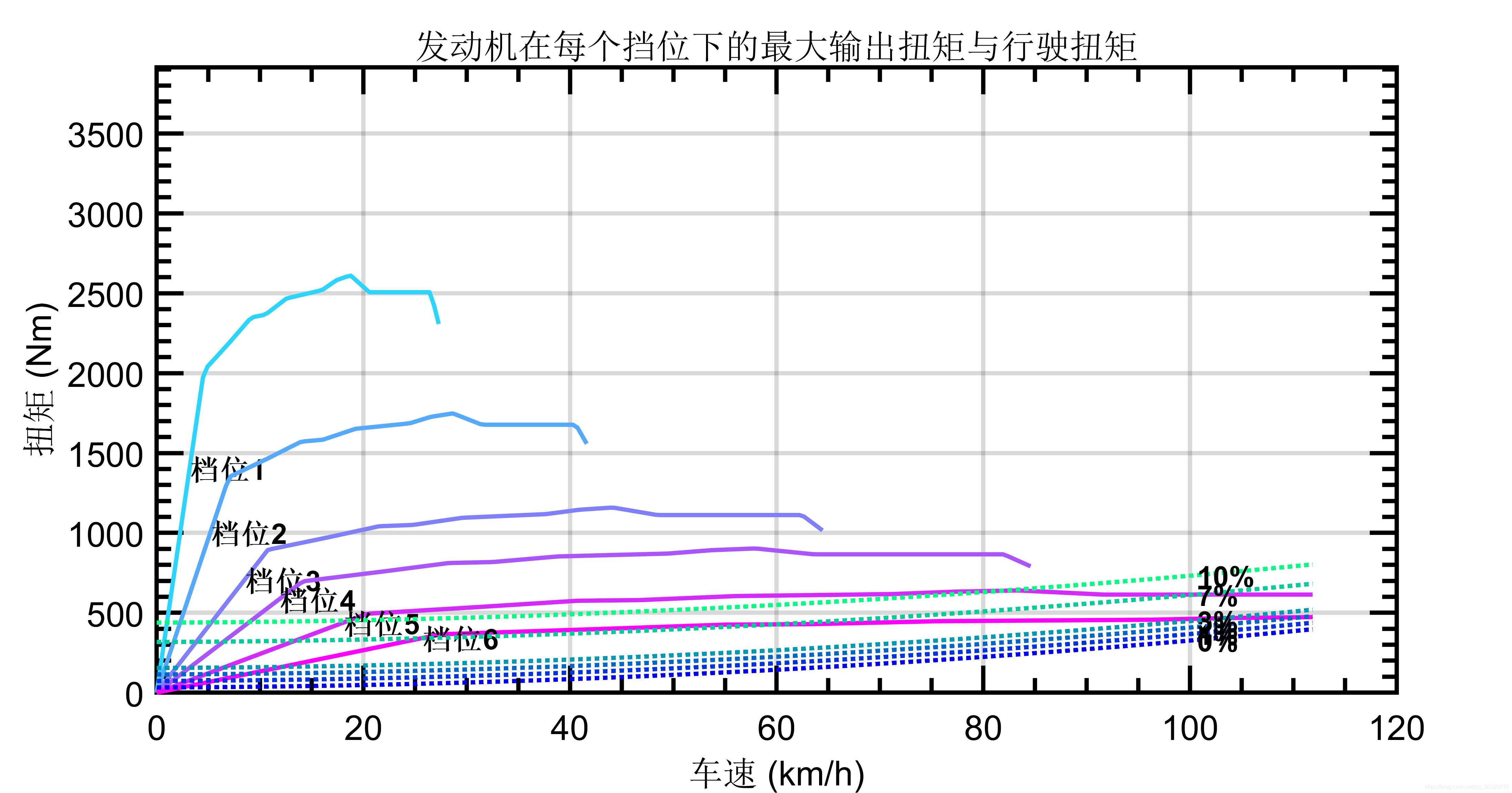
传统车绘制性能分析图像,包括各个档位下的发动机的最大外特性(车速与车轮处最大驱动扭矩/驱动力的关系),行驶阻力(不同坡度下)随车速的变化情况。根据输入绘图函数的类型,分别可绘制出驱动力(force)、驱动扭矩(torque)、驱动功率(power)等多种曲线。
绘制传统车动力性分析图需要提供的参数包括:
- 变速箱挡位个数;
- 主减速器与变速箱的传动效率
- 变速箱与主减速器速比
- 车轮半径
- 行驶阻力方程中涉及到的整车参数
由于力,扭矩,和驱动功率分别为 驱动力,驱动力X车轮半径,扭矩X转速,因此绘制不同曲线时,仅y轴求取的方式不同,绘制图形的主体不变。
绘制三(或多个)y坐标轴函数
该函数分布输入三条需要绘制的x,y向量,以及三个y轴的标签即可(或者不输入),该函数输出包括三个坐标轴的对象和包括三个曲线的对象。可对图像进一步设置和调整。
该函数首先利用plotyy绘制双y轴图像,然后将第三个y轴向右偏移一定的比例后,在对第三条曲线绘制。
例如采用以下测试代码绘制定制化的图像:
由于axes包含 line对象,figure对象又包含axes对象,对axes和 line对象进行合适的配置即可达到定制化的目的。
figure
pos = [0.1 0.1 0.7 0.8];
ax=axes('Position',pos,'box','off',...
'Color','none','XColor','k','YColor','r',...
'xtick',[],'yaxislocation','right');
line([0:0.1:2*pi],sin([0:0.1:2*pi]),'Parent',ax)
采用上述绘制后如下所示的图像:

function [ax,hlines] = plotyyy(x1,y1,x2,y2,x3,y3,ylabels)
%PLOTYYY - Extends plotyy to include a third y-axis
%
%Syntax: [ax,hlines] = plotyyy(x1,y1,x2,y2,x3,y3,ylabels)
%
%Inputs: x1,y1 are the xdata and ydata for the first axes' line
% x2,y2 are the xdata and ydata for the second axes' line
% x3,y3 are the xdata and ydata for the third axes' line
% ylabels is a 3x1 cell array containing the ylabel strings
%
%Outputs: ax - 3x1 double array containing the axes' handles
% hlines - 3x1 double array containing the lines' handles
%
%Example:
% x=0:10;
% y1=x; y2=x.^2; y3=x.^3;
% ylabels{1}='First y-label';
% ylabels{2}='Second y-label';
% ylabels{3}='Third y-label';
% [ax,hlines] = plotyyy(x,y1,x,y2,x,y3,ylabels);
% legend(hlines, 'y = x','y = x^2','y = x^3',2)
% %
if nargin==6
%Use empty strings for the ylabels
ylabels{1}=' '; ylabels{2}=' '; ylabels{3}=' ';
elseif nargin > 7
error('Too many input arguments')
elseif nargin < 6
error('Not enough input arguments')
end
figure('units','normalized',...
'DefaultAxesXMinorTick','on','DefaultAxesYminorTick','on');
%Plot the first two lines with plotyy
[ax,hlines(1),hlines(2)] = plotyy(x1,y1,x2,y2);
cfig = get(gcf,'color');
pos = [0.1 0.1 0.7 0.8];
offset = pos(3)/5.5;
%Reduce width of the two axes generated by plotyy
pos(3) = pos(3) - offset/2;
set(ax,'position',pos);
%Determine the position of the third axes
pos3=[pos(1) pos(2) pos(3)+offset pos(4)];
%Determine the proper x-limits for the third axes
limx1=get(ax(1),'xlim');
limx3=[limx1(1) limx1(1) + 1.2*(limx1(2)-limx1(1))];
ax(3)=axes('Position',pos3,'box','off',...
'Color','none','XColor','k','YColor','r',...
'xtick',[],'xlim',limx3,'yaxislocation','right');
hlines(3) = line(x3,y3,'Color','r','Parent',ax(3));
limy3=get(ax(3),'YLim');
%Hide unwanted portion of the x-axis line that lies
%between the end of the second and third axes
line([limx1(2) limx3(2)],[limy3(1) limy3(1)],...
'Color',cfig,'Parent',ax(3),'Clipping','off');
axes(ax(2))
%Label all three y-axes
set(get(ax(1),'ylabel'),'string',ylabels{1})
set(get(ax(2),'ylabel'),'string',ylabels{2})
set(get(ax(3),'ylabel'),'string',ylabels{3})
统计数据分布情况函数
该函数输入两个需要统计的向量,例如发动机转速随时间变化的向量和转矩随时间变化的向量,然后输入需要给出需要统计数据分布的类型,包括 ‘energy’ 和 ‘time’ 两种情况,分别代表能量分布和时间分布情况。
既然该函数是统计两个向量数据的分布情况,必然对这两个向量组成的xy平面进行划分,默认分别对x,y向量划分20块,然后统计划分xy后每一个小区域内的分布占比(时间或者能量占比)。因此该函数输出为x,y划分后的等间距向量x_index,y_index,以及统计分布情况 map_dens。利用这三个输出参数,即可绘制三维分布情况。
function [x_index,y_index,map_dens] = map_density_cal(x,y,type_dens)
% 初始化网格
N_x=20;
N_y=20;
x_index=linspace(min(x),max(x),N_x);
y_index=linspace(min(y),max(y),N_y);
x_radius=(x_index(2)-x_index(1))/2; % 每个 bin
y_radius=(y_index(2)-y_index(1))/2;
map_dens = zeros(N_x,N_y);
% 计算密度网格
for cpt_x=1:N_x
for cpt_y=1:N_y
idx_count=find((x>=(x_index(cpt_x)-x_radius)) & (x<(x_index(cpt_x)+x_radius))&(y>=(y_index(cpt_y)-y_radius)) & (y<(y_index(cpt_y)+y_radius)));
switch(type_dens)
case('time')
map_dens(cpt_x,cpt_y)=numel(idx_count)/numel(x)*100;
case('energy')
map_dens(cpt_x,cpt_y)=sum(abs(x(idx_count).*y(idx_count)))./sum(abs(x.*y))*100;
end
end
end
end