上次算法导论课讲到了Haffman树,笔者惊叹于Haffman编码的压缩效果,故想自己亲自动手尝试写一个极简的Haffman压缩程序。
首先,我们来了解一下什么是Haffman编码
Haffman编码
赫夫曼编码可以很有效地压缩数据:通常可以节省20%~90%的空间,具体压缩率依赖于数据的特性。我们将待压缩数据看做字符序列。根据每个字符的出现频率,赫夫曼贪心算法构造出字符的最优二进制表示。我们考虑一种二进制字符编码的方法,每个字符用一个唯一的二进制串表示,称为码字。如果使用定长编码,需要使用3位来表示6个字符:a=000,b=001,…,f=101。这种方法需要300000个二进制位来编码文件。是否有更好的编码方案呢?
变长编码(variable-length code)可以达到比定长编码好得多的压缩率,其思想是赋予高频字符短码字,赋予低频字符长码字。下图显示了本例的一种变长编码:1位的串0表示a,4位的串1100表示f。因此,这种编码表示此文件共需(45·1+13·3+12·3+16·3+9·4+5·4)· 1000=224000位,与定长编码相比节约了25%的空间。实际上,我们将看到,这是此文件的最优字符编码。

前缀码
我们这里只考虑所谓前缀码(prefix code),即没有任何码字是其他码字的前缀。虽然我们这里不会证明,但与任何字符编码相比,前缀码确实可以保证达到最优数据压缩率,因此我们只关注前缀码,不会丧失一般性。
任何二进制字符码的编码过程都很简单,只要将表示每个字符的码字连接起来即可完成文件压缩。例如,使用上图所示的变长前缀码,我们可以将3个字符的文件 abc编码为0·101·100-0101100, “·”表示连结操作。
前缀码的作用是简化解码过程。由于没有码字是其他码字的前缀,编码文件的开始码字是无歧义的。我们可以简单地识别出开始码字,将其转换回原字符,然后对编码文件剩余部分重复这种解码过程。在我们的例子中,二进制串001011101可以唯一地解析为0·0·101 · 1101,解码为aabe。
解码过程需要前缀码的一种方便的表示形式,以便我们可以容易地截取开始码字。一种二叉树表示可以满足这种需求,其叶结点为给定的字符。字符的二进制码字用从根结点到该字符叶结点的简单路径表示,其中0意味着“转向左孩子”,1意味着“转向右孩子”。下图给出了两个编码示例的二叉树表示。注意,编码树并不是二叉搜索树,因为叶结点并未有序排列,而内部结点并不包含字符关键字。
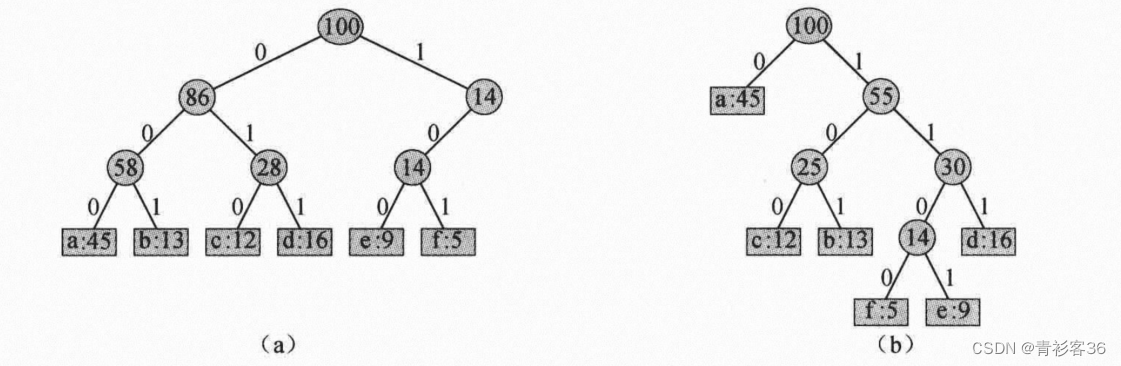
上图为图1中编码方案的二叉树表示。每个叶结点标记了一个字符及其出现频率。每个内部结点标记了其子树中叶结点的频率之和。(a)对应定长编码a=000,…,f=101的二叉树。(b)对应最优前缀码a=0,b=101,…,f=1100的二叉树
给定一棵对应前缀码的树T,我们可以容易地计算出编码一个文件需要多少个二进制位。对于字母表C中的每个字符c,令属性c. freq表示c在文件中出现的频率,令dT(c)表示c的叶结点在树中的深度。注意,dT(c)也是字符c的码字的长度。则编码文件需要
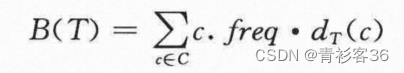
个二进制位,我们将 B(T)定义为T的代价。
Haffman树构造过程
我们假定C是一个n个字符的集合,而其中每个字符c∈C都是一个对象,其属性c. freq给出了字符的出现频率。算法自底向上地构造出对应最优编码的二叉树T。它从|C|个叶结点开始,执行|C|-1个“合并”操作创建出最终的二叉树。算法使用一个以属性 freq为关键字最小优先队列Q,以识别两个最低频率的对象将其合并。当合并两个对象时,得到的新对象的频率设置为原来两个对象的频率之和。
对前文给出的例子,赫夫曼算法的执行过程如下图所示。由于字母表包含6个字母,初始队列大小为n=6,需要5个合并步骤构造二叉树。最终的二叉树表示最优前缀码。一个字母的码字为根结点到该字母叶结点的简单路径上边标签的序列。
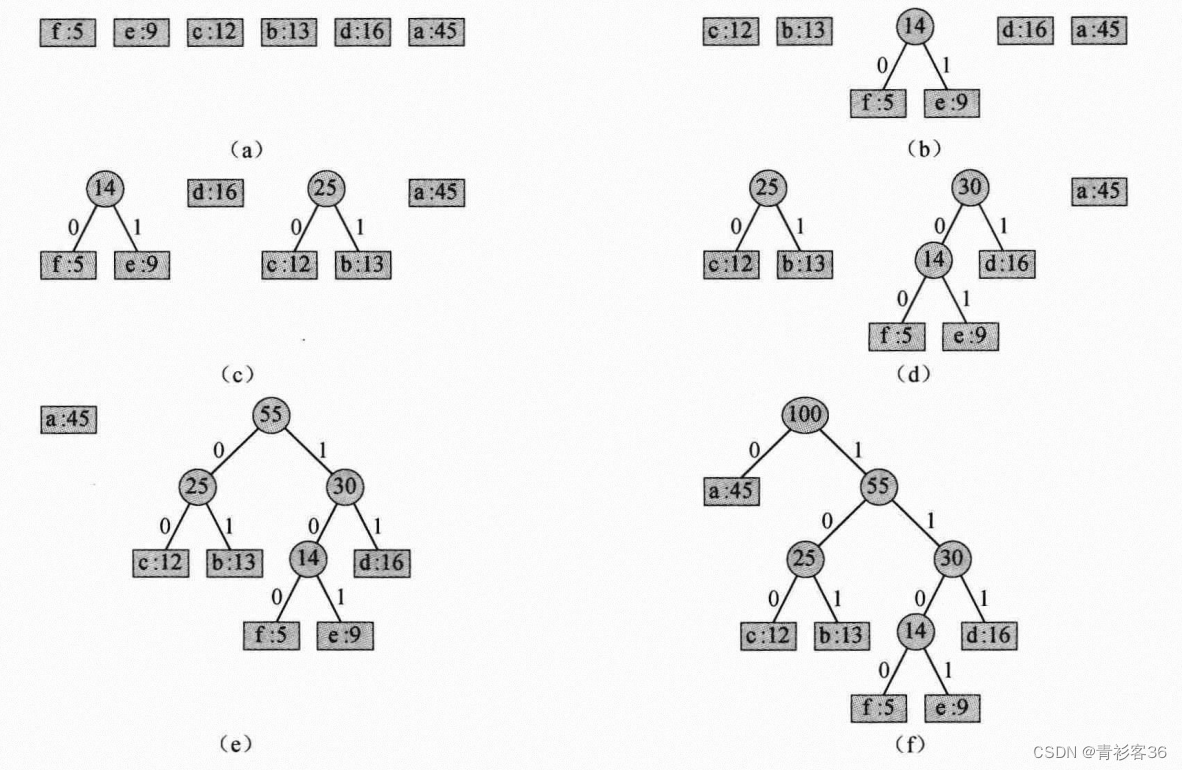
代码实现
哈夫曼编码压缩文件的主要思路:
1. 读取某个文本文件, 统计文件中各个字符出现的次数作为权重
2. 构建哈夫曼树, 生成每个字符对应的编码, 然后将编码保存到压缩文件中
3. 文件解压缩实际就是将压缩文件翻译过来再保存到解压缩文件的过程
HaffmanTree.h
#ifndef HAFFMANTREE_H_INCLUDED
#define HAFFMANTREE_H_INCLUDED
/**
* Haffman树的顺序存储
* 哈夫曼编码压缩文件的主要思路:
* 1. 读取某个文本文件, 统计文件中各个字符出现的次数作为权重
* 2. 构建哈夫曼树, 生成每个字符对应的编码, 然后将编码保存到压缩文件中
* 3. 文件解压缩实际就是将压缩文件翻译过来再保存到解压缩文件的过程
*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX_SIZE 256
#define HALF_MAX MAX_SIZE / 2
#define ASCII_SIZE 128 // ASCII码的数量0~127个字符
/** 哈夫曼树的结点 */
typedef struct haffNode
{
char data; // 用来存放结点字符的数据域
int weight; // 权重
struct haffNode * leftChild;
struct haffNode * rightChild;
} HaffNode;
/** 以顺序结构存储的树节点 - 编码解码的字符映射表 */
HaffNode node[MAX_SIZE];
/** 用来保存所有左孩子节点的数组*/
HaffNode left[HALF_MAX];
/** 用来保存所有右孩子节点的数组*/
HaffNode right[HALF_MAX];
/** 使用二维数组来存储字符的哈夫曼编码, 其中第一维的下标就是这个字符的ASCII码*/
char code[MAX_SIZE][HALF_MAX];
// char code[][] = {
// "00", "10", "1101", ......
// };
/**
* 构造哈夫曼树
* @param node 结点数组
* @param length 节点数组的长度
*/
void CreateHaffmanTree(HaffNode * node, int length);
/** 冒泡排序, 默认以权值大小降序排列*/
void SortHaffmanNode(HaffNode * node, int length);
/**
* 编码过程(压缩)
* @param node 结点数组
* @param tempCode 编码后的字符数组(keepCode)
* @param index 当前字符数组下标
*/
void Coding(HaffNode * node, char * tempCode, int index);
/** 解码过程 flag - 0/1 标志 */
HaffNode * unzip(HaffNode * node, int flag);
#endif // HAFFMANTREE_H_INCLUDED
HaffmanTree.c
#include "HaffmanTree.h"
/**
* 构造哈夫曼树
* @param node 哈夫曼树的(根)节点
* @param length 节点数组的长度
*/
void CreateHaffmanTree(HaffNode * node, int length)
{
if(length <= 1)
{
return ;
}
SortHaffmanNode(node, length);
// 构建一个以node数组最后两个结点组成的父节点
HaffNode parent; // 声明一个父节点
left[length] = node[length - 1]; // 排序后, length-1就是权重最小的结点
right[length] = node[length - 2]; // length-2就是权重次小的结点
parent.weight = left[length].weight + right[length].weight;
parent.leftChild = &left[length];
parent.rightChild = &right[length];
// parent 结点的data不用赋值
// 将倒数第二位替换为parent结点, 数组长度减一, 递归创建哈夫曼树
node[length - 2] = parent;
CreateHaffmanTree(node, length - 1);
}
/**
* 编码过程(压缩)
* @param node 结点数组
* @param tempCode 编码后的字符数组(keepCode)
* @param index 当前字符数组下标
*/
void Coding(HaffNode * node, char * tempCode, int index)
{
if(!node) return ;
// 处理叶节点 - 所有的字符结点都是叶子结点
if(node->leftChild == NULL || node->rightChild == NULL)
{
// 将编码赋值到编码数组中去
tempCode[index] = '\0';
strcpy(code[node->data - 0], tempCode);
return ;
}
// 左分支编码为'0', 右分支编码为'1'
tempCode[index] = '0';
Coding(node->leftChild, tempCode, index + 1);
tempCode[index] = '1';
Coding(node->rightChild, tempCode, index + 1);
}
/** 解码过程 flag - 0/1 标志 */
HaffNode * unzip(HaffNode * node, int flag)
{
if(flag == 0)
{
return node->leftChild;
}
else if(flag == 1)
{
return node->rightChild;
}
return NULL;
}
/** 冒泡排序, 默认以权值大小降序排列*/
void SortHaffmanNode(HaffNode * node, int length)
{
HaffNode tempNode;
for(int i = 0; i < length - 1; ++ i)
{
for(int j = 0; j < length - i - 1; ++ j)
{
if(node[j].weight < node[j + 1].weight)
{
tempNode = node[j];
node[j] = node[j + 1];
node[j + 1] = tempNode;
}
}
}
}
注:此处没有按照算法导论上说的那样,使用优先队列(实际上就是堆嘛),笔者使用了最简单的冒泡排序,每次将最小的两个数合并之后,调用一次冒泡排序,读者可在此处进行扩充,改用堆排序或直接使用C++ STL中的优先队列hh~
main.c
#include <stdio.h>
#include <stdlib.h>
#include "HaffmanTree.h"
int main()
{
unsigned char saveChar = 0; // 保存到二进制文件的无符号字符
unsigned char tempChar;
printf("使用哈夫曼树实现文本文件的压缩: (暂时只支持英文文件)\n");
FILE * inputFile = fopen("pride-and-prejudice.txt", "r"); // 待解码文件
FILE * zipedFile = fopen("ziped.txt", "wb"); // 编码压缩后的文件
int fileLength = 0; // 文件中存放的字符个数
// 存放0-127个字符出现的次数 - 权数组
int asciiCount[ASCII_SIZE] = {0};
// 读取待编码的文件, 统计各字符出现的次数
char readChar;
// 逐字符读取文件
while((readChar = fgetc(inputFile)) != EOF)
{
fileLength ++;
// 读取到的字符就作为asciiCount数组的下标
asciiCount[readChar - 0] ++;
}
int num = 0; // 节点数量(计数器)
for(int i = 0; i < ASCII_SIZE; ++ i)
{
if(asciiCount[i] != 0)
{
node[num].data = i;
node[num].weight = asciiCount[i];
num ++;
}
}
// 创建哈夫曼树
CreateHaffmanTree(node, num);
// 进行哈夫曼编码
char tempCode[HALF_MAX];
Coding(node, tempCode, 0);
// 逐位将编码保存到文件zipedFile中
num = 0;
fseek(inputFile, 0L, 0); // 文件指针复位
int zipedLength = 0; // 压缩后的字符数量
// 遍历读取到的这个字符编码("10", "111", "1101" ......)
while((readChar = fgetc(inputFile)) != EOF)
{
for(int i = 0; i < strlen(code[readChar - 0]); ++ i)
{
saveChar |= code[(int)readChar][i] - '0';
num ++;
if(num == 8)
{ // 每8位写入一次文件
fwrite(&saveChar, sizeof(unsigned char), 1, zipedFile);
zipedLength ++;
num = 0;
saveChar = 0;
}
else
{
saveChar <<= 1;
}
}
}
// 如果最后剩余的编码不足8位, 就移动到最左端, 凑够8位
if(num < 8)
{
saveChar = saveChar << (8 - num);
fwrite(&saveChar, sizeof(unsigned char), 1, zipedFile);
zipedLength ++;
saveChar = 0;
}
fclose(inputFile);
fclose(zipedFile);
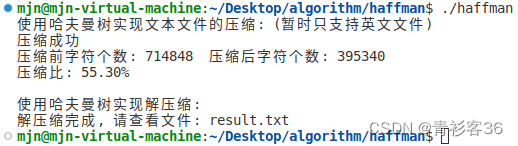
printf("压缩成功\n压缩前字符个数: %d\t压缩后字符个数: %d\n", fileLength, zipedLength);
printf("压缩比: %.2f%%\n", (double)zipedLength / fileLength * 100);
printf("\n使用哈夫曼树实现解压缩: \n");
zipedFile = fopen("ziped.txt", "rb");
FILE * resultFile = fopen("result.txt", "w");
num = 0; // 计数器清零
HaffNode * currNode = &node[0];
while(fread(&readChar, sizeof(unsigned char), 1, zipedFile))
{
if(fileLength == num) break;
// 遍历readChar中的每个二进制数字
for(int i = 0; i < 8; ++ i)
{
tempChar = readChar & 128; // 取readChar得最高位
tempChar >>= 7;
readChar <<= 1; // 因为最高位已经被取, 所以左移1位
currNode = unzip(currNode, tempChar - 0);
// 判断叶节点
if(currNode->leftChild == NULL || currNode->rightChild == NULL)
{
fprintf(resultFile, "%c", currNode->data);
num ++;
currNode = &node[0];
}
}
}
fclose(zipedFile);
fclose(resultFile);
printf("解压缩完成, 请查看文件: result.txt\n");
return 0;
}