学习步骤：

如果我要学习等比数列，我会按照以下步骤进行学习：

1. 定义和性质：首先了解等比数列的定义和性质，包括公比、首项、通项公式、求和公式等。

2. 例题练习：通过练习一些简单的例题来理解等比数列的概念和性质，并能够灵活应用公式解决问题。

3. 深入理解：通过更深入的学习，理解等比数列的本质和特点，掌握等比数列的一些重要性质和结论。

4. 拓展应用：将等比数列应用到实际问题中，例如金融、物理、工程等领域，进一步提升应用能力。

5. 练习题和考试题：通过练习一些难度适中的练习题和考试题，巩固所学知识，提高解题能力。

在学习等比数列时，需要注意以下几点易错点：

1. 计算公比时，需要注意首项和第二项的关系，特别是当首项为0或负数时。

2. 在求等比数列的和时，需要根据等比数列的性质进行变形，注意不要混淆等比数列的通项公式和求和公式。

3. 当涉及到无穷等比数列时，需要特别注意收敛和发散的条件。

4. 在应用等比数列解决实际问题时，需要注意将问题转化为等比数列的形式，并结合具体问题进行分析和求解。

总的来说，学习等比数列需要掌握其基本概念和性质，熟练应用其相关公式，深入理解其本质和特点，同时注意常见易错点和解题技巧。

 

 

 

 

 

 

 

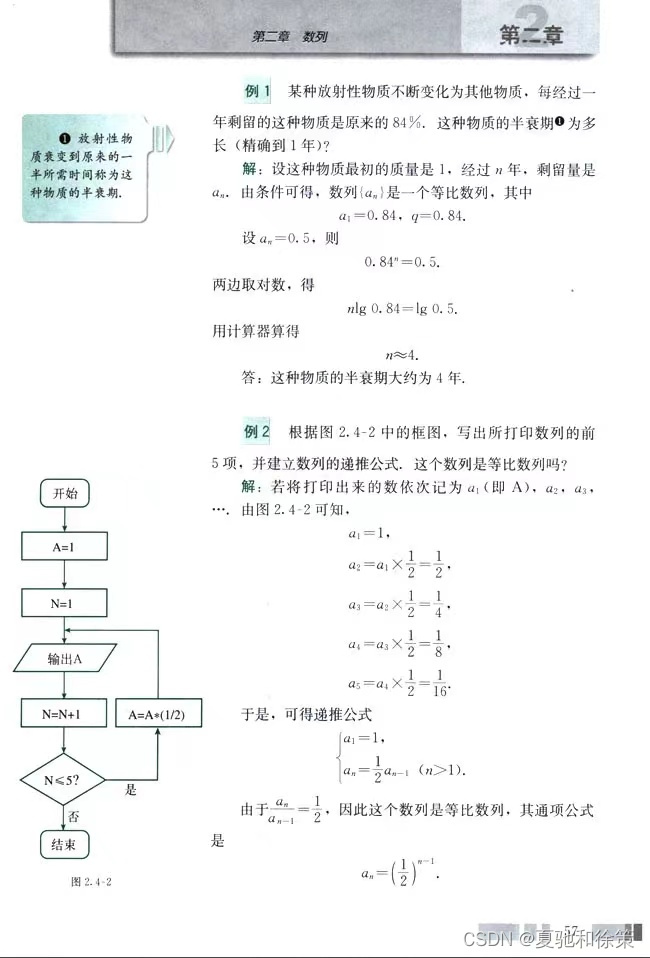
 (此处等比数列求和中无穷的概念便是他与高等数学直接联系)

重点：

等比数列是数列中的一种，它的相邻两项之比为常数，这个常数称为公比。在学习等比数列时，重点、难点和易错点如下：

重点：

1. 等比数列的定义和性质，如公比、首项、通项公式、求和公式等。

2. 等比数列的基本运算，如求某一项的值、求前n项和等。

3. 等比数列与其他数学概念的联系，如指数函数、对数函数等。

难点：

1. 当公比小于1时，等比数列的前n项和具有极限，需要进行证明。

2. 当公比为负数时，等比数列的部分性质会发生变化，需要注意处理。

3. 等比数列的应用，需要根据具体问题进行建模和分析，常常需要一定的创造性思维和解决问题的能力。

易错点：

1. 计算公比时，需要注意首项和第二项的关系，特别是当首项为0或负数时。

2. 在求等比数列的和时，需要根据等比数列的性质进行变形，注意不要混淆等比数列的通项公式和求和公式。

3. 当涉及到无穷等比数列时，需要特别注意收敛和发散的条件。

4. 在应用等比数列解决实际问题时，需要注意将问题转化为等比数列的形式，并结合具体问题进行分析和求解。

总的来说，掌握等比数列需要了解其基本定义和性质，熟练掌握其运算和应用，深入理解其本质和特点，同时注意常见易错点和解题技巧。