学习不是一次性的投资，而是一份长期稳定的收益。

8位锁存器

上篇文章讲到了1位存储器的组成，将8个1位存储器的时钟端连在一起就形成了一个8位锁存器，如下所示：

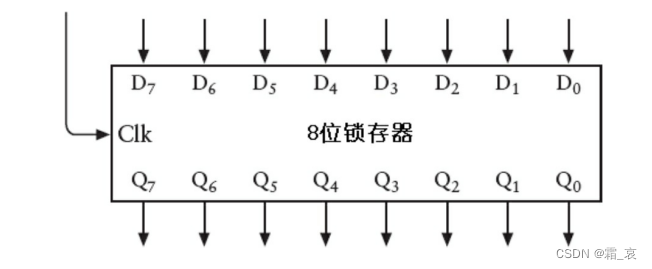
这个锁存器一次存储八位，由统一的时钟端进行管理。为了深入理解这个结构，我们用这个结构实现一个连加的加法器。
连加的原理就是将每次相加的结果存储起来作为下一次进行加法运算的加数。具体电路实现如下：

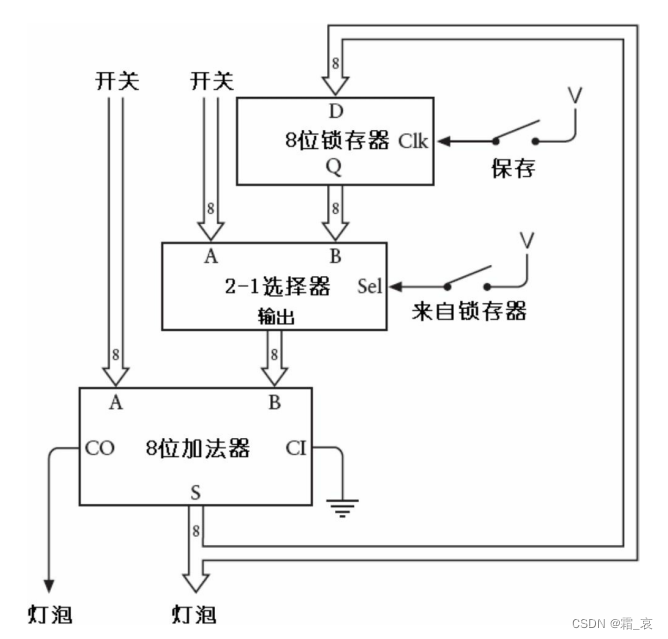
其中，2-1选择器从两个8位输入中选择一个作为输出与左侧的A相加。这个选择器电路组成如下：

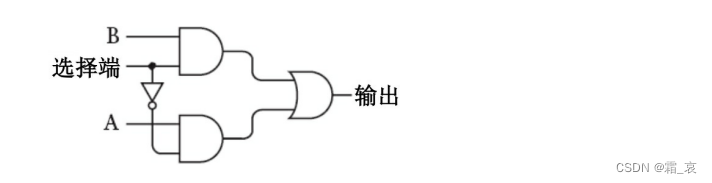
看一下这个电路的运作过程：

1. 2-1选择器选择A输出作为B输入和左边的A输入相加，输出结果
2. 结果传输到右上角D处进行存储，输出到Q被选择器选择，在进入加法器进行相加操作
3. 重复过程。

可以发现，这个加法器处理不了进位符号的累加，但这个问题我们之后再讲，先看一下这个电路的改进。
不难发现，这个电路中锁存器的左边输入只需要用到一次，这样的话，我们能不能省去这八个开关呢？答案是可行的。但在此之前，我们需要为锁存器加一个清零开关，如下图所示：

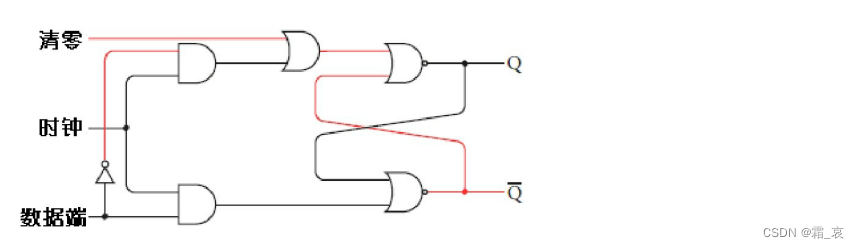
打开这个清零开关，可以让这个锁存器的输出一定为0。当然，也可以通过把时钟置1，数据端置0的方法使输出为0，但很显然，在加法器中我们不能决定锁存器的数据端输入，所以只能通过这个方法。
接下来，我们可以通过调换加法器和锁存器的顺序省去一组开关，如下图所示：

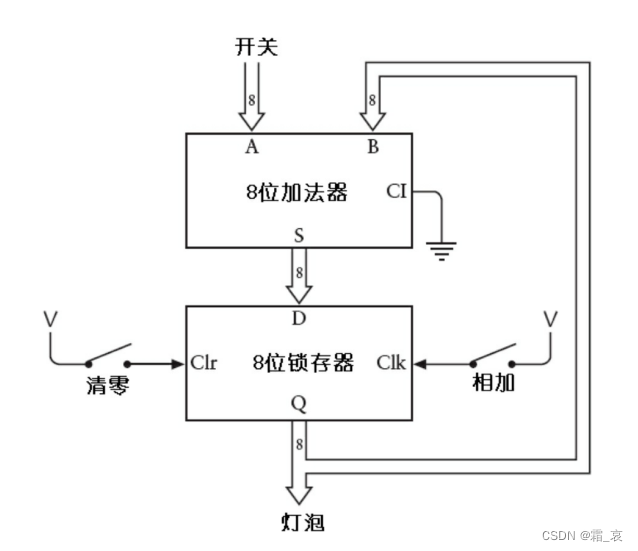
边沿触发器

边沿触发器在时钟端从0到1变化的一瞬间存储数据。其电路如下：

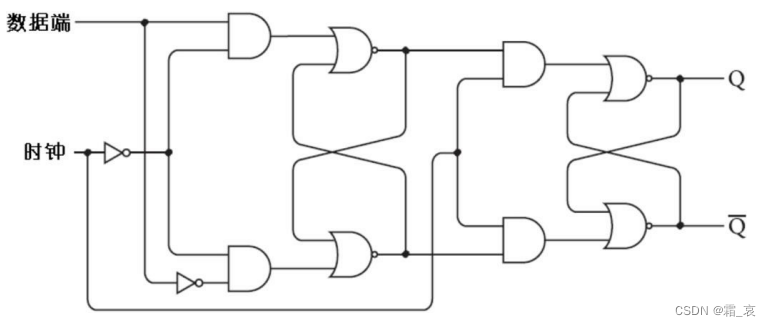
边沿触发器实际上就是两个R-S触发器串联，一个时钟信号同时控制两个触发器，但在第一级触发器取反。同时数据端的输入只在第一级取反，以达到和电平触发器相同的输出。
看一下这个电路存储数据的过程：

1. 时钟端置0，数据端置1，数据传入第一级触发器。
   
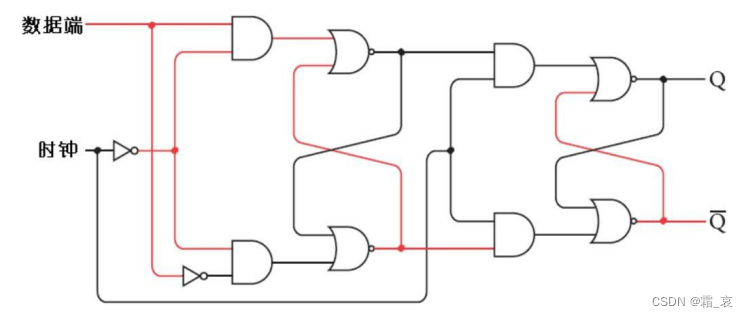
2. 接下来时钟端置1，第一级触发器的时钟输入变为0，像当于把数据存储进第一级触发器；同时第二级触发器时钟输入变为1，数据传入第二级触发器并在输出上显示。
   
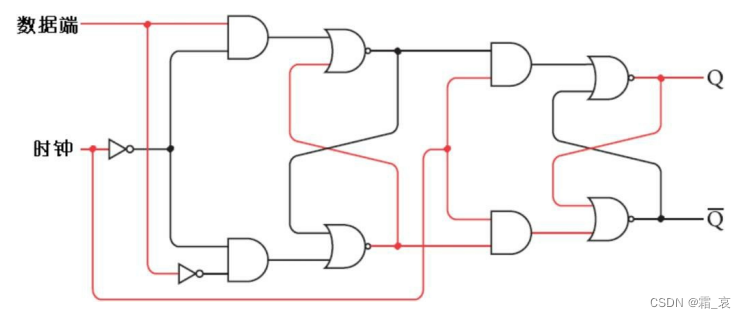
3. 数据端置0，由于第一二级触发器已经存储了数据端的数据，因此电路不变。注意：此时即使时钟端变为0，数据依然会存储在电路中。
   

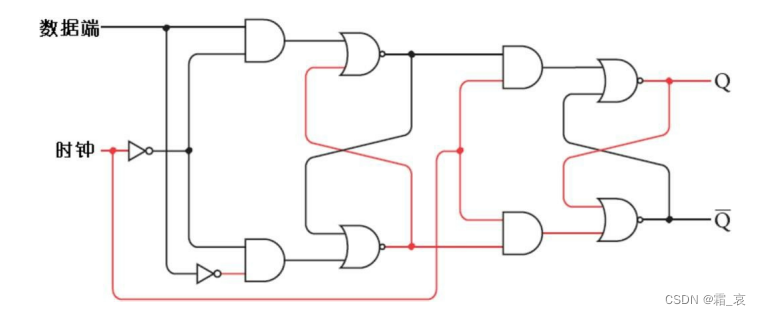
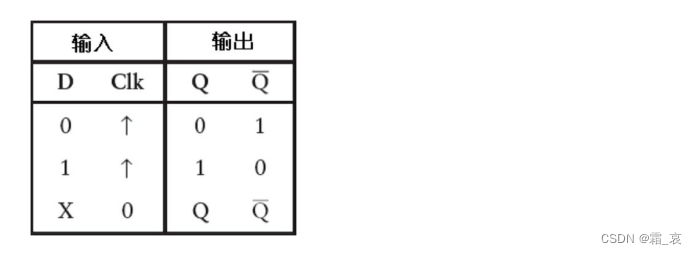
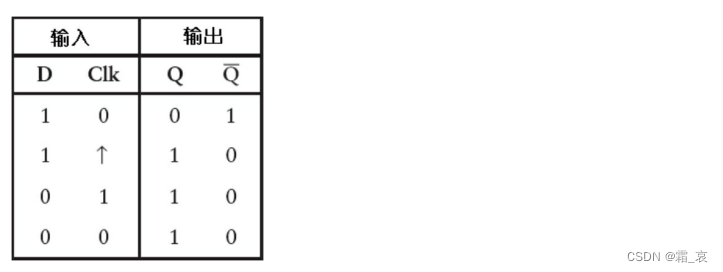
到此这个电路的运作原理也介绍完毕，看一下它的真值表（⬆表示电压从0到1的正跳变）：

边沿触发器的符号如图所示，小三角表示这是一个边沿触发器：

计数器

显然，将边沿触发器连接一个振荡器的话，它会周期性的改变输出：

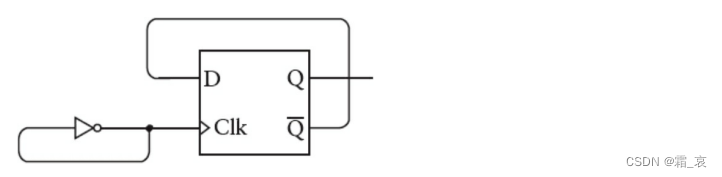
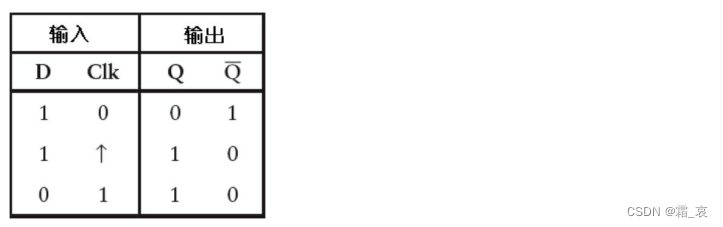
在这个电路中，振荡器周期性的01切换，且每次¬Q变化后都会变化。看一下这个电路的变化过程：

1. 假设启动时时钟端输入为0，D输入为1。
   

2. 时钟正跳变，输出随数据端D改变。
   

3. 由于¬Q变为0，则D变为0，但此时跳变结束，输出数据不改变。
   

4. 时钟输入变为0，负跳变不影响输出。
   

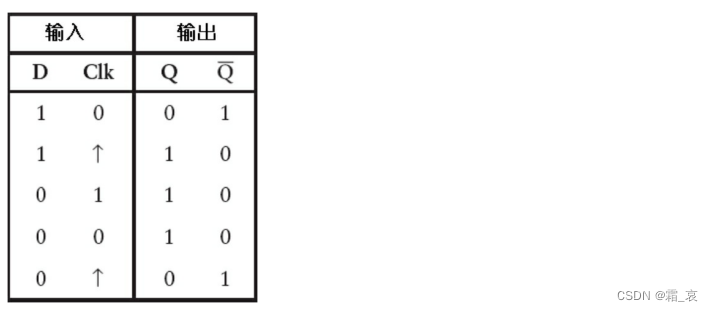
5. 继续正跳变，输出随D变化。
   

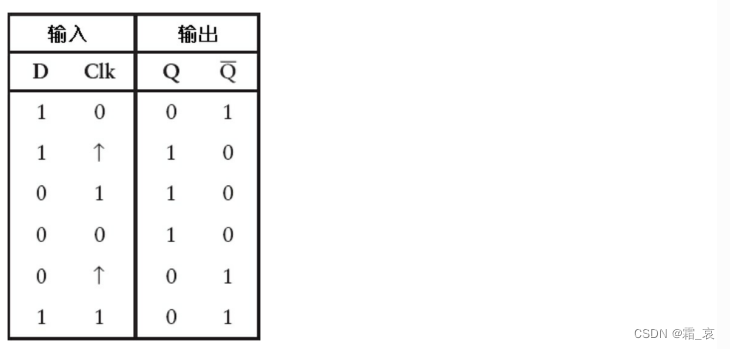
6. ¬Q变为1，D随之改变为1。
   

7. 时钟负跳变，回到最开始的状态。

时钟端和输出端呈周期性变化，由于每次时钟端负跳变时输出端不变，只有正跳变时才变化，因此输出端的变化周期是时钟端的2倍：

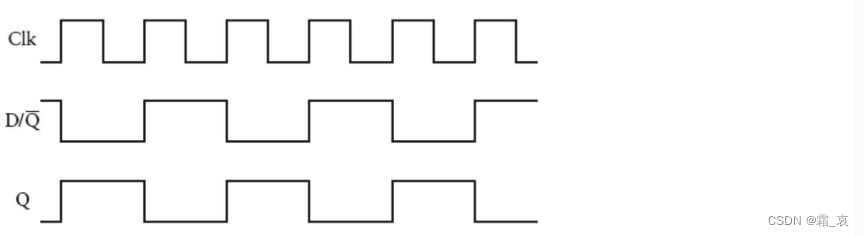
想象一下，如果把多个边沿触发器串联起来，将前面触发器的输出端作为后面触发器时钟端的输入，那么每一个触发器的周期都是前一个的2倍，这种电路称为分频器：


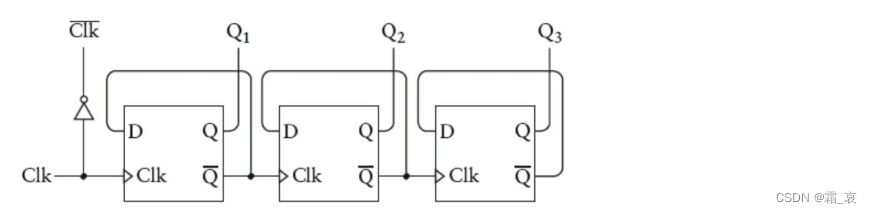
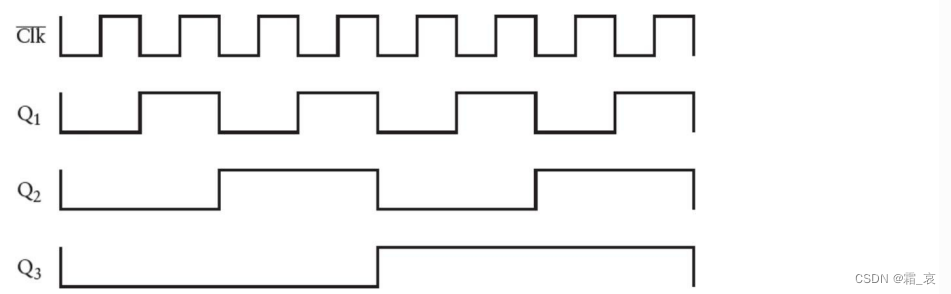
尝试着写一下从0-15的二进制数，你会发现每前一个二进制位从0到1的周期都是后一位的2倍，与这个电路的规律相同。因此这个电路可以做一个计数器，每次时钟信号正跳变或负跳变时计数加1。
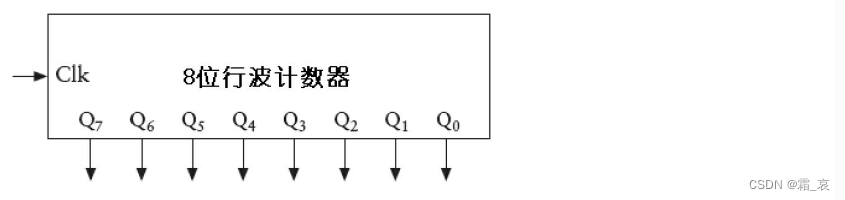
在实际操作中，我们将第一个触发器的输出作为最后一个二进制位，那么将8个边沿触发器串联起来，就是一个八位行波计数器，这种计数器的缺点是电路一级一级传递，到最后一级时会有延迟。下面是八位行波计数器的符号：

改进的边沿触发器

和电平触发器相同，边沿触发器也可以加上预置和清零开关，而且原理和普通边沿触发器相同，我们只是简要介绍。下面是这种触发器的电路表示：

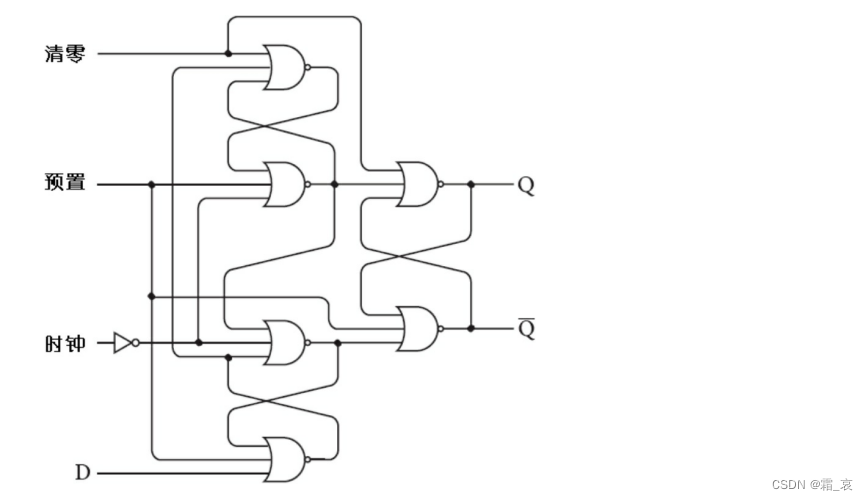
预置信号让Q为1，¬Q为0；清零信号让Q为0，¬Q为1。
这是边沿触发器的符号表示：


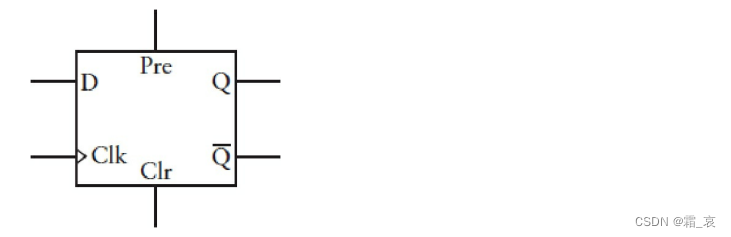
我是霜_哀，在算法之路上努力前行的一位萌新，感谢你的阅读！如果觉得好的话，可以关注一下，我会在将来带来更多更全面的知识讲解！