文章目录
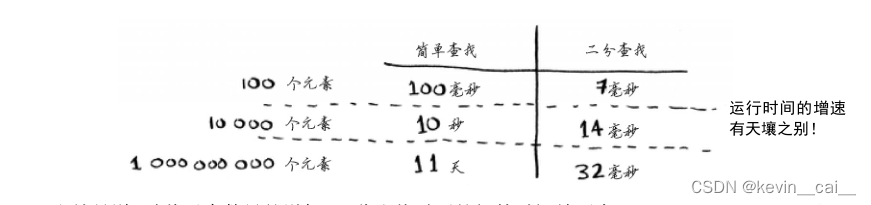
- 一、算法的效率
- 1.1 如何衡量一个算法的好坏
- 1.2 算法的复杂度的概念
- 二、大O的渐进表示法
- 三、时间复杂度
- 2.1 时间复杂度的概念
- 2.2常见时间复杂度计算举例
- 四、空间复杂度
- 2.1 空间复杂度的概念
- 2.2常见空间复杂度计算举例
- 五、解决问题的思路
- LeetCode-exercise
- 总结
一、算法的效率
1.1 如何衡量一个算法的好坏
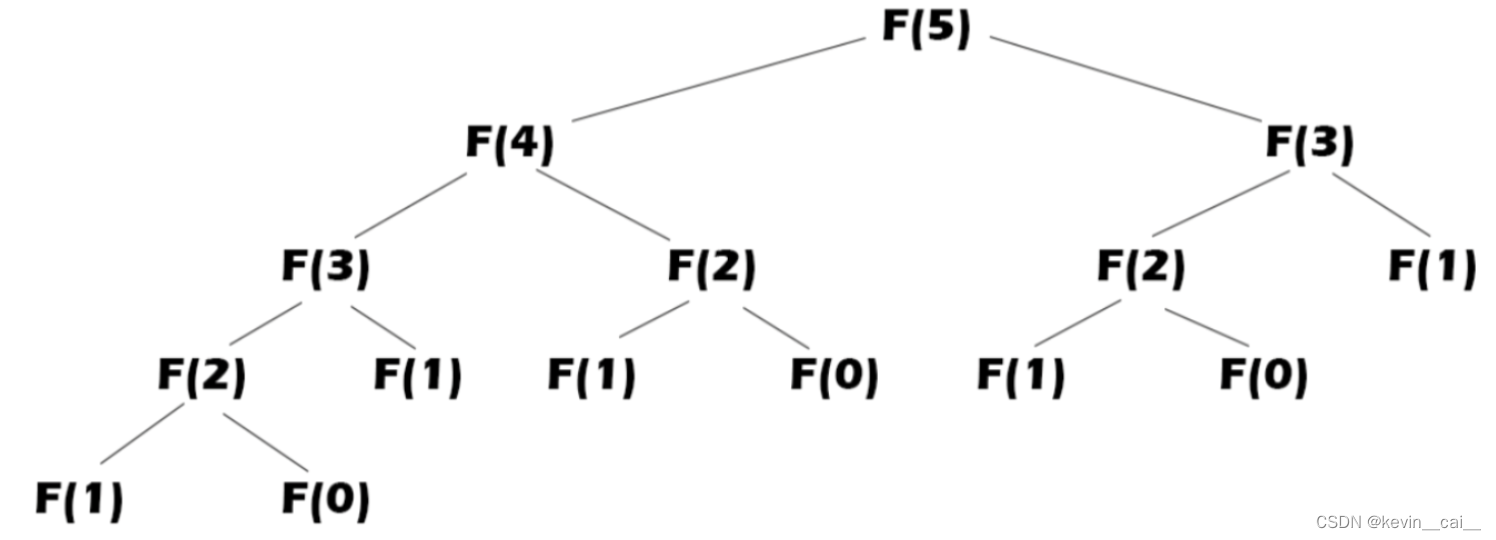
如何衡量一个算法的好坏呢?比如对于以下斐波那契数列:
long long Fib(int N)
{
if(N < 3)
return 1;
return Fib(N-1) + Fib(N-2);
}
- 这里的时间复杂度为:2^N,计算方法请看下文。
- 算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
1.2 算法的复杂度的概念
- 一般而言分析算法效率的方式有两种,即:时间效率和空间效率。时间效率也称为时间复杂度;空间效率也称为空间复杂度。
- 在计算机技术发展的几十年中,空间资源变得不是非常重要了,因此在一般的算法分析中,讨论的主要是时间复杂度,当然空间复杂度的分析也是如此。
- 时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。
二、大O的渐进表示法
- 大O符号是由德国数论学家保罗·巴赫曼(Paul Bachmann)在其1892年的著作《解析数论》(Analytische Zahlentheorie)首先引入的。
- “大O符号(Big Onotation)是用来描述函数渐进行为的数学符号”,假设原有的函数程序执行步为T(n),那么当T(n)=O(f(n))时,当且仅当存在正常数C和n0,使得T(n)≦C*f(n)对于所有n,n≧n0都成立。其中的f(n)这个函数用来描述原来的函数的数量级的渐进上界。使用大O符号时,用的O代表无穷大的渐进,它表示n趋近于无穷大时的一种情况。此时我们把O(f(n))称为算法的渐进时间复杂度,简称时间复杂度。时间复杂度的渐进上界表示如下图所示:
- 当问题规模即要处理的数据增长时, 基本操作要重复执行的次数必定也会增长, 那么我们关心地是这个执行次数以什么样的数量级增长。所谓数量级可以理解为增长率。这个所谓的数量级就称为算法的渐近时间复杂度(asymptotic time complexity), 简称为时间复杂度。
- 食用方法:
1.用常数1来取代运行时间中所有加法常数。
2.修改后的运行次数函数中,只保留最高阶项
3.如果最高阶项存在且不是1,则去除与这个项相乘的常数。
4.在实际中一般情况关注的是算法的最坏运行情况。
三、时间复杂度
2.1 时间复杂度的概念
- 概念:算法的时间复杂度是一个函数,它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述(大O渐近表示法),不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,亦即考察输入值大小趋近无穷时的情况。
- 一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
- 通俗的说,因为计算机的计算能力特别强,所以我们只需要对算法执行次数进行估算,然后再进行优化,就能有效提高算法的效率。我们只需要关心量级,而不用关心具体执行次数。
- 实例:
2.2常见时间复杂度计算举例
实例1:
void Func(int N, int M)
{
int count = 0;
for (int k = 0; k < M; ++ k)
{
++count;
}
for (int k = 0; k < N ; ++ k)
{
++count;
}
printf("%d\n", count);
}
答案:执行了M+N次,未知数M+N,最坏就是(M+N)次,数量很大,所以时间复杂度为O(M+N)
实例2:
long long Fib(size_t N)
{
if(N < 3)
return 1;
return Fib(N-1) + Fib(N-2);
}
答案:O(2^N)
四、空间复杂度
2.1 空间复杂度的概念
概念:空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少bytes的空间,因为对现在计算的存储容量来说也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表示法。
2.2常见空间复杂度计算举例
实例1:
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
答案: O(1)
实例2:O(N)
long long Fib(size_t N)
{
if(N < 3)
return 1;
return Fib(N-1) + Fib(N-2);
}
答案:O(N)
五、解决问题的思路
LeetCode-exercise
- 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
旋转数组
通过上面的学习,我们不难发现
- 思路一:一步一步进行旋转,其时间复杂度是O(K*N),空间复杂度为O(1) 。
- 思路二:创建新数组,分三步走旋转,其时间复杂度为O(N),空间复杂度为O(N)。
- 思路二通过空间换时间,提高了算法效率,对于如今的计算机来说,极大地存储容量,浪费的这一点空间完全是值得的。
//思路一的实现:
void rotate(int* nums, int numsSize, int k) {
int tmp = 0;
while (k >= numsSize)
{
k %= numsSize;
}
for (int i = 0; i < k; i++)
{
tmp = nums[numsSize - 1];
for (int j = 0; j < numsSize - 1; j++)
{
nums[numsSize - 1-j] = nums[numsSize - 2-j];
}
nums[0] = tmp;
}
}
//思路二的实现:
void rotate(int* nums, int numsSize, int k){
k %= numsSize;
//变长数组
int tmp[numsSize];
//后k个拷贝前面
int j = 0;
for(int i = numsSize-k ; i < numsSize ; ++i)
{
tmp[j] = nums[i];
++j;
}
//前n-k拷贝到后面
for(int i = 0; i < numsSize-k ; ++i)
{
tmp[j] = nums[i];
++j;
}
//拷贝回去
for(int i = 0 ; i < numsSize ; ++i)
{
nums[i] = tmp[i];
}
}
总结
- 学习了数据结构以后,遇到问题的时候,我们不应该直接暴力求解,而是通过思考不同的解决方案,估算其时间复杂度和空间复杂度,选择最优解以提升算法效率。
- 先思考,再求解。
- 小伙伴们都学废了吗?












![【群智能算法】一种改进的蜣螂优化算法IDBO[2]【Matlab代码#18】](https://img-blog.csdnimg.cn/be6bbacb0981451bb3f3eea12a48fec9.png)