不少高校的小伙伴找我聊入门人工智能该怎么起步,如何快速入门,多长时间能成长为中高级工程师(聊下来感觉大多数学生党就是焦虑,毕业即失业,尤其现在就业环境这么差),但聊到最后,很多小朋友连人工智能和机器学习、深度学习的关系都搞不清楚。
今天更文给大家科普一下这三者是什么及他们之间的关系,希望能帮到大家
人工智能
人工智能(Artificial Intelligence,简称 AI)这个词学术上是如何定义的呢?
美国麻省理工学院温斯顿教授认为:“人工智能就是研究如何使计算机去做过去只有人才能做的智能工作。另外有说“限制人工智能发展的是人的想象力”更使人工智能技术蒙上了一层浩瀚伟大的神秘外衣
人工智能的发展将会彻底改变人类的生产和生活方式,随之而来的是社会对人才需求的改变,即:就业趋势会逐渐偏向 AI 领域。
事实上,人工智能已经在各行各业的发展中扮演着重要的角色,并且它的地位还在不断地提升。
例如:人脸识别、自动驾驶、智能客服、短视频推荐、金融风控、智慧医疗、智慧农业、机器人技术等,这些都是人工智能在各个行业中的具体应用。
人工智能是一个不断发展和变化的领域,它是一个真正充满希望的行业。人工智能一方面使得其它职业容易被替代,另一方面也增加了 AI 技术人员的不可替代性。
接下来,聊一下机器学习与深度学习的概念以及它们和人工智能的关系,这是许多刚接触 AI 这个领域的人最容易混淆的几个概念。
机器学习
首先,什么是机器学习?它和人工智能有什么关系呢?
机器学习(Machine Learning,简称 ML)是从大量的经验数据中学习一种规律(或者称之为模型),从而实现人类所具备的一些能力。
举个栗子吧,比如我可以根据一个人的身高去预测他的体重,一定是因为我见过很多的人,并且了解了他们的身高和体重,才会有一个比较合理的判断。
那么我的这种判断能力可以让计算机学会吗?答案是肯定的。机器学习是人工智能的一种实现方式,也是最重要的实现方式。
首先,我们需要收集大量的身高和体重数据,然后根据这些数据画一个散点图:
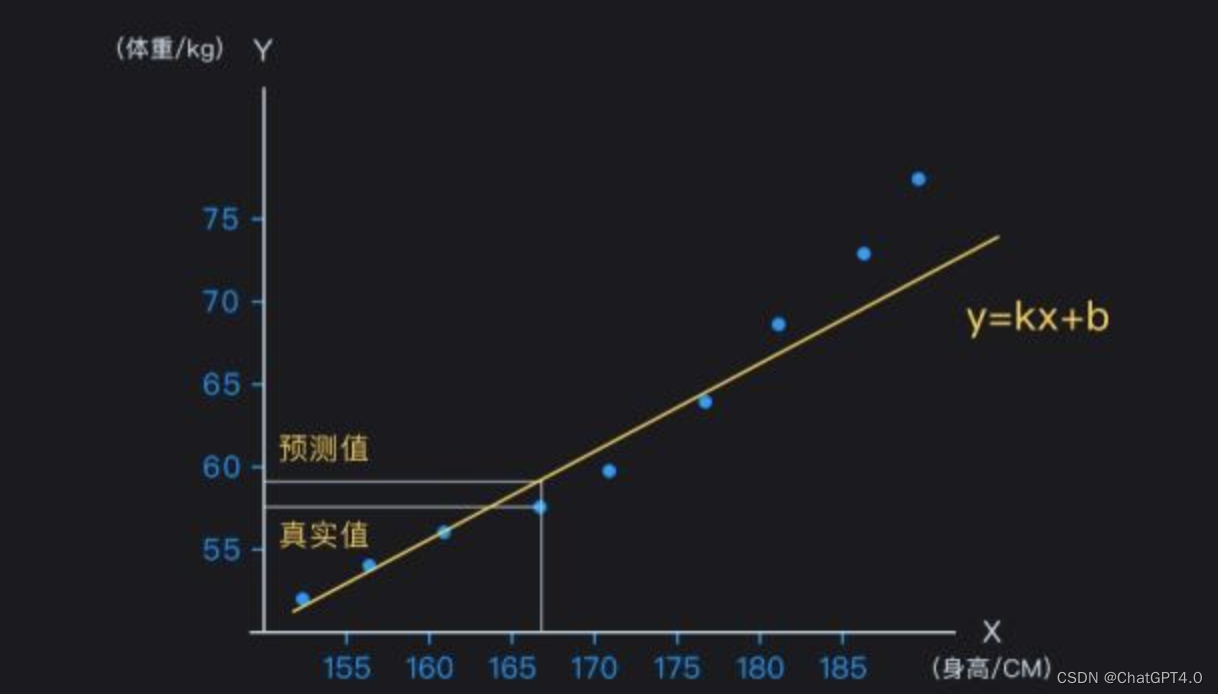
仔细观察,身高和体重的关系其实可以用高中所学的一次线性函数 f(x) = kx+b 来近似刻画,我们假设数据符合这样的规律,然后让计算机从数据中学习到函数的参数 k 和 b。
这里的 f(x) 可以理解为机器学习中的模型,换句话说,模型本质上是一个数学上的函数,也可以称之为从输入到输出的映射。
请你思考一个问题:计算机是如何从数据中学习到参数 k 和 b 的呢?
你可能会想到高中学过的一次线性函数的解法:先根据两点坐标确定斜率,然后得到点斜式直线方程。那么,计算机是这么做的吗?
计算机可不是这么解的。首先,选择哪两个点来确定斜率就是个问题。因为这些数据点并不是严格的一次线性关系,我们是用 f(x) = kx + b 来近似刻画数据的规律,所以计算机要做的是让这个近似的函数最大程度地拟合数据,进而使得误差最小化。
这其实也引出了机器学习的方法:最小化误差函数。这里的误差函数在机器学习中的术语叫做 经验风险或结构风险 。至于如何最小化,这又是一个知识点了,涉及到最优化算法。在后面的课程中,我会详细讲解经验风险、结构风险以及基本的最优化算法。
模型参数学习的思路是:先初始化参数 k 和 b,然后把数据点 (x,y) 的横坐标 x 代入一次线性函数得到预测值 f(x),根据预测值 f(x) 与真实值 y 的误差去调整参数,直到整体误差足够小时,停止学习。如图所示:

这幅图反映了模型 y=kx+b 对蓝色数据点的拟合情况,假如学习到的模型是 y = 0.34x+2,我们就可以根据 y = 0.34x + 2 来预测未知身高 x 对应的体重值 y了。
综上所述,机器学习本质上是数据驱动下的学习,而人类学习是靠过往的经验去学习。
AI、ML、DL的关系
我们经常听到的是深度学习(Deep Learning ,简称 DL)和人工智能这两个词。那么深度学习与人工智能有什么关系呢,机器学习和深度学习哪个概念的范畴更大一些呢?
答案是机器学习的范畴更大一些。具体来讲,深度学习是机器学习现在比较火的一个方向,其本身是神经网络算法的衍生,在图像、语音等富媒体的分类和识别上取得了非常好的效果。
所以,深度学习也是人工智能的一种重要的实现方式。下面这张图反映了AI、ML、DL 的从属关系和研究范畴大小:
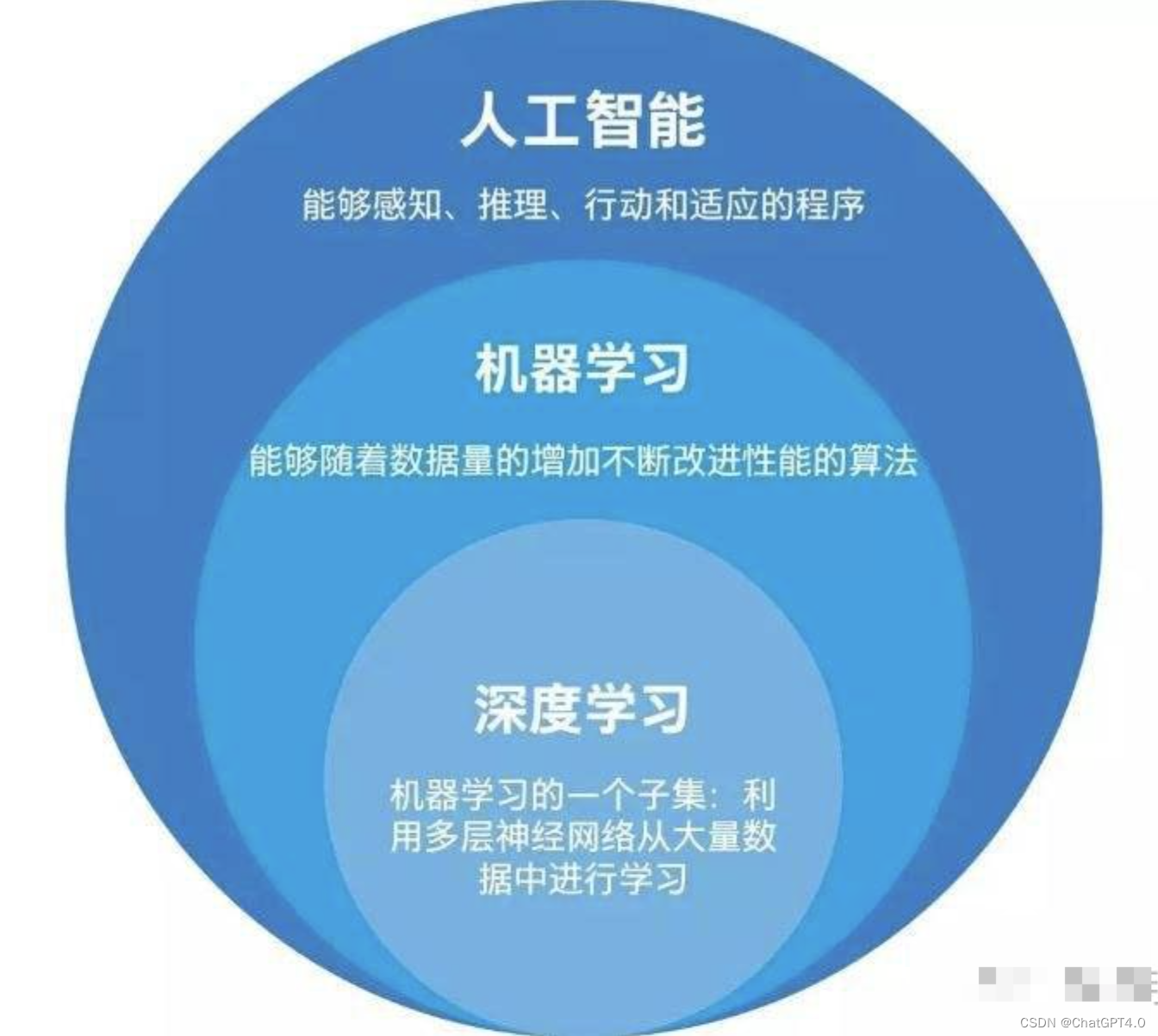
如果你有更简洁更合理的说法欢迎交流。