文章目录
- 1. 原始DBO算法
- 2. 改进后的IDBO算法
- 2.1 Bernoulli混沌映射种群初始化
- 2.2 自适应因子
- 2.3 Levy飞行策略
- 2.4 动态权重系数
- 3. 部分代码展示
- 4. 效果图展示
- 5. 资源获取
1. 原始DBO算法
详细介绍此处略,可参考DBO算法介绍
2. 改进后的IDBO算法
2.1 Bernoulli混沌映射种群初始化
传统的蜣螂优化算法在种群初始化阶段采用的是生成随机数的方式进行初始化种群位置,导种群中蜣螂的位置良莠不齐,同时不能遍历环境中的所有位置,导致其寻优效果差、收敛速度低。所以本文提出在种群初始化阶段引入Bernoulli映射,Bernoulli映射的数学表达式可表示为:
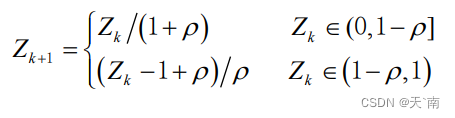
其中,
Z
k
Z_{k}
Zk为产生的第
k
k
k代混沌序列的当前值,
ρ
\rho
ρ为控制参数,经过实验发现,当
ρ
\rho
ρ处于 0.5 附近时能够获得更好的遍历性。
2.2 自适应因子
在繁殖和觅食行为的蜣螂位置更新公式中,会根据目前的个体和群体的最优解来更新自己的位置,一旦这个解陷入局部最优,整个种群就很容易进入停滞状态,为了改善这个问题,平衡全局和局部搜索能力,引入了自适应因子:
k = 2*rand()-1;
z = exp(5*cos(pi*(t/Max_iteration)));
c = exp(z*k) * cos(2*pi*k);
2.3 Levy飞行策略
在偷窃行为蜣螂的位置更新公式中,也会根据目前的个体最优值来更新自己的位置,也容易陷入局部最优,此时可以使用莱维飞行策略进行位置更新使得这部分个体去到更广的搜索空间:

2.4 动态权重系数
基本蜣螂优化算法的偷窃行为更新阶段,在迭代初期就向全局最优解逼近,会导致搜索范围不足,陷入局部最优,使搜索失败。为克服这一弊端,再在其位置更新公式中加入动态权重系数 ω,让它在迭代初期具有较大值,促进
全局搜索,迭代后期自适应变小,促进局部搜索并加快收敛速度。
3. 部分代码展示
function [ bestX,fMin , Convergence_curve ] = HDBO(N, Max_iteration,lb,ub,dim,fobj )
P_percent = 0.2;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
pNum = round( N * P_percent ); % The population size of the producers
lb= lb.*ones( 1,dim ); % Lower limit/bounds/ a vector
ub= ub.*ones( 1,dim ); % Upper limit/bounds/ a vector
%Initialization
% ★★改进1:Bernoulli映射种群初始化★★
x = Bernoulli(N,dim,ub,lb);
for i = 1 : N
fit( i ) = fobj( x( i, : ) ) ;
end
pFit = fit;
pX = x;
XX=pX;
[ fMin, bestI ] = min( fit );
bestX = x( bestI, : );
4. 效果图展示

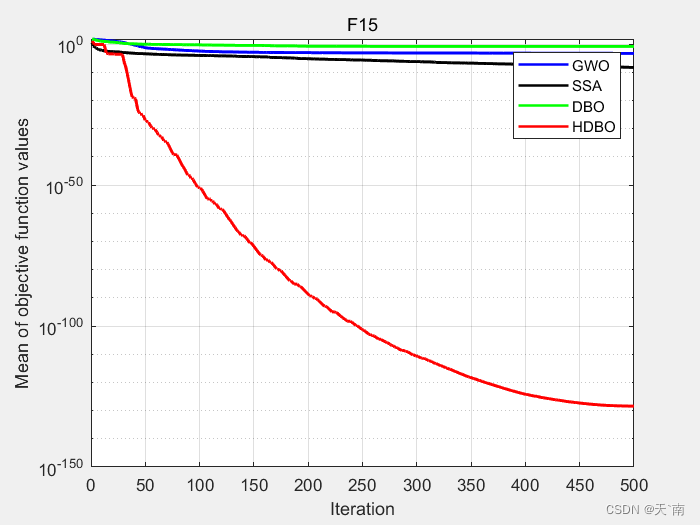
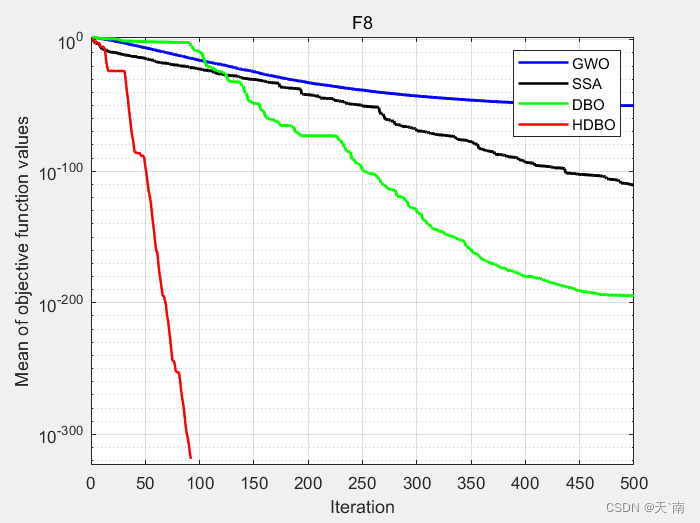

5. 资源获取
A资源获取说明.zip
A资源获取说明.zip