数量性状的遗传率/遗传力(heritability)
(1)表型值及其方差的分量
1. 表型值及其剖分
某数量性状的表型值就是实际所度量或观察到的数值。表型值受许多外界因素如士壤、肥力、水分、光照、温度等的改变而发生变异,这种变异归因于环境因素。任何一个数量性状的表现都是遗传和环境共同作用的结果
所以形状的表型值首先可以剖分为遗传和环境两个组成部分:
P = G + E
其中:P = 表型值;G = 基因型值;E = 环境效应
人的“身高”是一种典型的数量性状,是由多基因的遗传与环境效应共同作用的结果。人类正常身高表型呈正态分布,最高个体及最矮个体出现的频率很低,处在正态分布的两端。我国篮球名将姚明罕见的身高为2.29 m比他的家乡上海男性同期平均身高 (1.68 )高出接近0.61m,高出36.3%。

对公式 P= G +E 中的基因型值进一步剖分,其由3部分组成
- 基因的累加效应(additive effect,A):许多微效基因的累加效应造成的遗传变异,能遗传且固定的组分,又称“育种值”,即表示在动、植物育种工作中实际能够获得的效应。
- 显性离差(dominance deviation,D):等位基因之间若有显隐性关系,因而造成一些不同于累加效应的情况。由于基因在不同世代中的分离和重组,基因间的关系亦会发生变化,显性离差被认为是能遗传而不能被固定的遗传效应
- 互作离差或上位效应(interaction 或epistatic deviation,I):由于非等位基因之间的相互作用对于基因型值所产生的效应,是一种非加性的基因作用,称为互作或上位效应。由于非等位基因间的关系比较复杂,在作遗传分析时常常将其归于环境效应之内,作为环境效应的一部分,连同显性离差在内通称为剩余值(residualvalue,R),即除育种值之外,剩余的数值,这样我们用符号表示时,有:
G =A+D+I 因为 R=D+I+E,所以P=A+R
2. 表型方差及其分量
在群体中,某数量性状的遗传变异属于总的表型变异的一部分表型变异的其余部分是环境变异。在统计学上用方差作为变异的度量。总的表型方差可剖分为遗传方差和环境方差,于是:
总的表型方差 = 遗产方差 + 环境方差
所以:Vp(表型方差)=VG(遗传方差/基因型方差)+VE(环境方差)
如果环境与基因型有互作
则: Vp = VG + VE + 2 COV(GE) ##GE为下标
若G与E不想管
则: Vp = VG + VE
因为基因型方差的组分有:
加性方差
显性方差
互作方差

其中:
VA:=加性方差 (育种值方差) 。由于多基因的累加效应造成的遗传变异,能遗传且固定的组分。
VD=显性方差。由于等位基因间的显隐性关系而造成的一部分非加性的遗传变异,随着自交代数的增加而逐渐消失,所以能遗传但不能固定,是一种杂种优势现象。
Vi=互作方差。由于非等位基因之间上下位关系所产生的非加性的遗传变异,此分量也被认为能遗传而不能固定。
遗传力(遗传率,heritability)
所谓遗传力就是遗传变量在总的表现变量所占的比值,通常它式用百分率(%)来表示的
① 广义遗传力(heritability in the broad sense,H²)
指数量性状基因型方差占表型方差的比例,用公式表示为:

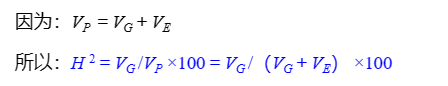
通过广义遗传力的估计,可以了解一个性状受遗传效应影响有多大受环境效应影响多大。
② 狭义遗传力(heritability in the narrow sense, h²)
是指数量性状育种值方差(加性方差)占表型方差的比例:

由于育种值是从基因型效应中已剔除显性效应和上位效应后的加性效应部分,在世代传递中是可以稳定遗传的,因此它在育种上具有重要意义.
- 某数量性状的遗传率大,说明在该数量性状的表现中,由遗传所决定的比率较大,环境对它的影响较小.
- 通常,与生物适应性无关的性状往往比与适应性有关的性状的遗传率要高一些 .
-
- 适应性是指生物体与环境表现相适合的现象。适应性是通过长期的自然选择,需要很长时间形成的。
- 应激性的结果是使生物适应环境,可见它是生物适应性的一种表现 …
- 但生物体的有些适应特征(如北极熊的白色、绿草地中蚱蜢呈绿色等等)是通过遗传传给子代的。并非生物体接受某种刺激后才能产生,这与应激性是不同的。
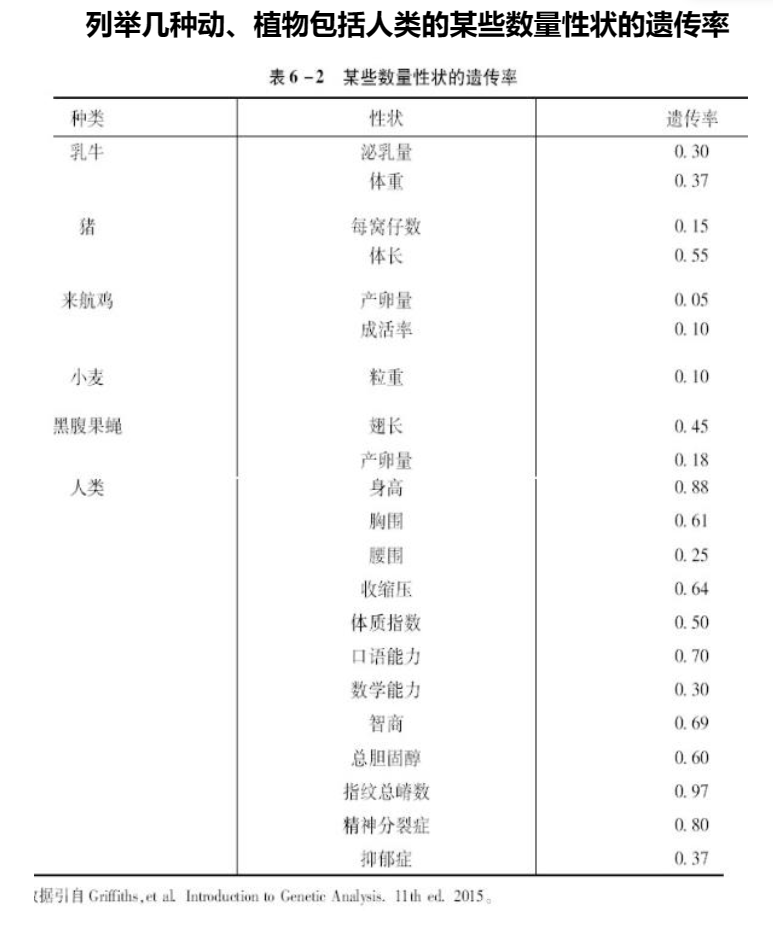
估计遗传率的方法
在自花授粉作物中根据不同来源的资料估计农作物数量性状遗传率的经典方法大致可以分为下列4种
- 利用基因型一致的不分离群体(纯合亲本和其F1群体),估计环境方差,求广义遗传率
- 用不同世代杂种群体消去环境方差和遗传方差中属于显性作用的方差,从而估计遗传方差中纯属于基因累加作用的方差,求狭义遗传率👈加性方差
- 利用上下代,亲代一子代的回归或相关关系估计狭义遗传率
- 用方差分析法分别估计总方差中各种方差组分,求遗传率
(1)人类疾病遗传率的估计
计算人类多基因遗传病遗传度的高低在临床实践上有重要意义,传统的计算方法主要有两种,即Falconer公式和Holzinger公式。
① Falconer公式
从群体和患者亲属发病率估计遗传率
Falconer1965年提出Falconer公式(Falconer method) ,它是根据先证者亲属的患病率与遗传率有关而建立的。亲属患病率越高,遗传率越大,所以可通过调查先证者亲属患病率和一般人群的患病率,算出遗传率(h2或H)

(1)式中,h²为遗传率;b为亲属易患性对先证者易患性的回归系数r为亲属系数
当已知一般人群的患病率时,用下式计算回归系数:

当缺乏一般人群的患病率时,可设立对照组,调查对照组亲属的患病率,用下式计算回归系数:
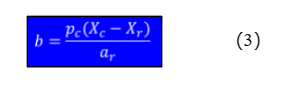
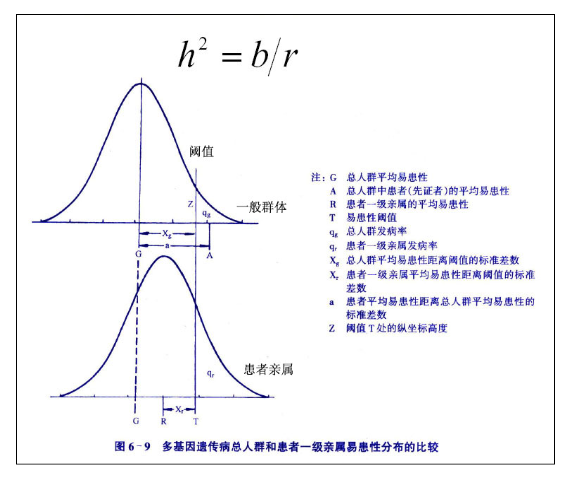
Falconer公式中各符号的意义:





在亲属系数中,一级亲属指一个人与其双亲、子女和同胞之间,其基因有1/2的可能性是相同的;二级亲属指一个人与其叔、伯、姑、舅、姨、祖父母和外祖父母之间,其基因有1/4的可能性是相同的;三级亲属指一个人与其表兄妹、堂兄妹、曾祖父母之间,其基因有1/8的可能性是相同的。
例如,有人调查先天性房间隔缺损在一般群体中的患病率为1/1000(0.1%),在100个先证者的家系中调查,先证者的一级亲属共有669人(双亲200人,同胞279人,子女190人),其中有22人发病,依次求得先证者一级亲属的患病率为22/669x100% =3.3% (q),然后查Falconer表。按群体患病率查得Xg和a,再根据亲属患病率查得Xr和ar,然后代入公式(2)求出b值.


② Holzinger公式--从双生子的发病一致率估计遗传率
Holzinger公式(Holzinger formula)(1929)是根据遗传率越高的疾病,一卵双生的患病一致率与二卵双生患病一致率相差越大而建立的
一卵双生(monozygotictwin,MZ)是由一个受精卵形成的两个双生子,他们的遗传基础理论上是完全相同的,其个体差异主要由环境决定,二卵双生(dizygotictwin,DZ)是由两个受精卵形成的两个双生子,相当于同胞,因此他们的个体差异由遗传基础和环境因素共同决定
所谓患病一致率是指双生子中一个患某种疾病,另一个也患同样疾病的频率
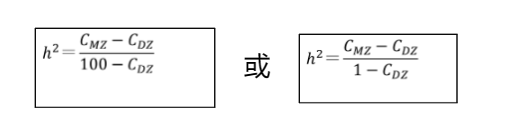
其中,Cmz为一卵双生子的同病率;CDz为二卵双生子的同病率
例如,对躁狂抑郁性精神病的调查表明,在15对单卵双生子中,共同患病的有10对;在40对双卵双生子中,共同患病的有2对。依此来计算单卵双生子的同病率为67%,双卵双生子的同病率为5%。代入上式:
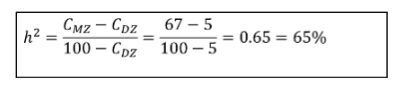
以上结果表明,在躁狂抑郁性精神病中,遗传素的贡献为65%
(2)复杂性疾病的再发风险估计
主要因素:群体发病率和遗传度(heritability)
遗传度的含义是多基因累加效应在复杂性疾病发生中的作用大小.通常用(%)表示.
对遗传度的说明
- 是一个统计学概念,针对群体而不是用于个体
- 相对特定的群体而言,如果遗传变异更改,或者环境变异更改,所得的遗传度自然也随之更改.
- 遗传度的估算仅适合于没有遗传异质性,也没有主基因效应的疾病
-
- 异质性是指一种遗传性状可以由多个不同的遗传物质改变所引起。
- 遗传异质性(genetic heterogeneity)是指某一种遗传疾病或表型可以由不同的等位基因或者基因座突变所引起的现象。在遗传学的现象中,基因型决定表型,但表型相同的个体,可能具有不同的基因型,即一种性状可以由多个不同的基因控制。遗传异质性分为等位基因异质性(是指同一基因,不同突变)和基因座异质性(是指不同基因,不同突变)。
- 控制数量性状的各对基因的效应大小不同,效应大的基因称之为主基因;效应小的基因称之为微效基因或多基因。主基因是指对数量性状能产生明显表型效应的基因


例如:
我国人群中,唇裂+腭裂的患病率为0.17%,其遗传度为76%,患者一级亲属的发病率:
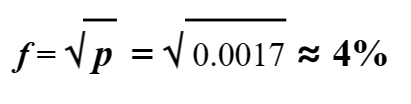
影响多基因遗传病再发风险的因素
1.累积效应
一个家庭中患病人数越多,意味着再发风险越高
2.病情严重程度于发病风险
多基因病中基因的累加效应还表现在病情的程度上。因为病情严重的患者必定带有更多的易感基因,其父母也会带有较多的易感基因使易患性更接近闯值
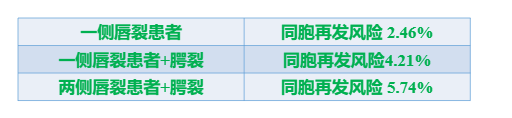
3.性别与发病风险
某种多基因遗传病的发病存在两性差异时,表明不同性别的发病闯值是不同的。群体发病率较低即闯值较高那个性别的个体患病,则患者亲属的发病风险较高。
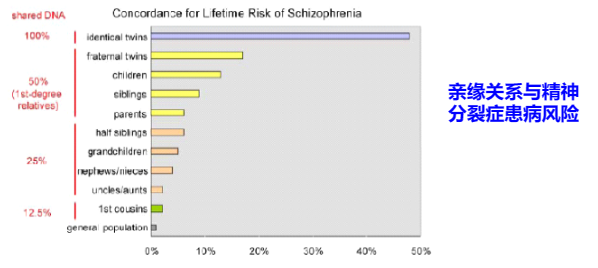
亲缘关系与发病风险
多基因遗传病有家族聚集倾向,患者亲属发病率高于群体发病率,但亲属发病率随着与先证者的亲缘关系级数递增而剧减,向着群体发病率靠扰。
希望能帮到你~

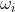





![[Data structure]单链表 | 一文介绍线性数据结构之一的单链表(Java实现)](https://img-blog.csdnimg.cn/f4eedcae0aa84f9084a0ac893f9494e1.png)