模块3-2 图形变换
一 实验目的
- 编写图形各种变换的算法
二 实验内容
1:任意直线的对称变换。要求将变换矩阵写在实验报告中,并与代码匹配。求对任意直线Ax+By+C=0的对称变换矩阵。
实验结果如下图所示:

1:预设图形初始化

2:鼠标左键点击直线起点

3:鼠标右键点击直线终点
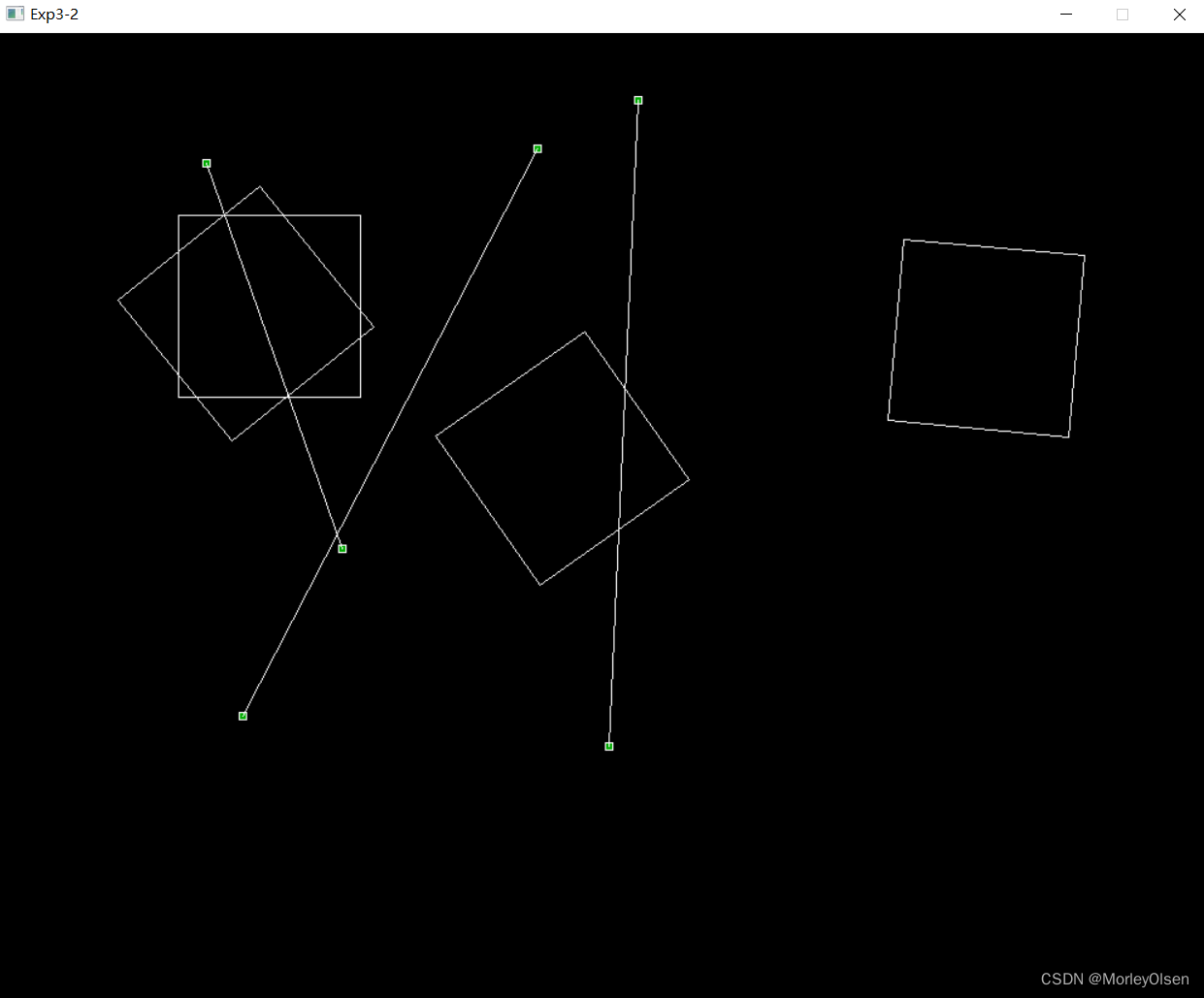
4:继续添加对称情况
求对任意直线Ax+By+C=0的对称变换矩阵:
对于任意直线Ax + By + C = 0,对称变换矩阵为M = (1-2A^2/(A^2+B^2), -2AB/(A^2+B^2), -2AC/(A^2+B^2); -2AB/(A^2+B^2), 1-2B^2/(A^2+B^2), -2BC/(A^2+B^2); 0, 0, 1),其中A和B不同时为0。
| 1-2A^2/(A^2+B^2) | -2AB/(A^2+B^2) | -2AC/(A^2+B^2) |
| -2AB/(A^2+B^2) | 1-2B^2/(A^2+B^2) | -2BC/(A^2+B^2) |
| 0 | 0 | 1 |
三 程序说明
最终的实验代码如下表所示:
| 1题 |
| // // 程序名称:任意直线对称变换 // 功 能:实现图形以任意直线为基准的对称变换 // 编译环境:VS2019,EasyX_20220116 // 最后修改:2022-4-7 #include <graphics.h> #include <conio.h> #include <iostream> #include <math.h> using namespace std; double points[4][2] = { {150,150},{150,300},{300,300},{300,150} }; const double newpoints[4][2] = { {150,150},{150,300},{300,300},{300,150} }; int num = 4, dimension = 3; #define PI 3.1415927 //旋转变换 void rotate(double degree); //平移变换 void trans(double tx, double ty); //矩阵乘法 void mutiply(double a[5][5], int ar, int ac, double b[5][5], int br, int bc); //画图函数 void paint(); //任意对称变换 void anysymmetry(int x1, int y1, int x2, int y2); //坐标轴对称变换 void symmetry(int flag); void anysymmetry(int x1, int y1, int x2, int y2) { double k = 0, b = 0; if (x1 == x2) { trans(-x1, 0); symmetry(1); trans(x1, 0); } else if (y1 == y2) { trans(0, -y1); symmetry(0); trans(0, y1); } else { k = 1.0 * (y1 - y2) / (x1 - x2); b = y1 - k * x1; trans(0, -b); rotate(-atan(k) * 180 * 1.0 / PI); symmetry(0); rotate(atan(k) * 180 * 1.0 / PI); trans(0, b); } } void symmetry(int flag) { int i; if (flag == 0) { for (i = 0; i < num; i++) { points[i][1] = -points[i][1]; } } else if (flag == 1) { for (i = 0; i < num; i++) { points[i][0] = -points[i][0]; } } else { return; } } void paint() { for (int i = 0; i < num; i++) { if (i == num - 1) { line(int(points[i][0]), int(points[i][1]), int(points[0][0]), int(points[0][1])); break; } line(int(points[i][0]), int(points[i][1]), int(points[i + 1][0]), int(points[i + 1][1])); } } void rotate(double degree) { double sita = 1.0 * degree / 180 * PI; double R[5][5] = { {cos(sita),-sin(sita),0},{sin(sita),cos(sita),0},{0,0,1.0} }; double point[5][5]; int i; for (i = 0; i < num; i++) { point[0][0] = 1.0 * points[i][0]; point[1][0] = 1.0 * points[i][1]; point[2][0] = 1; mutiply(R, dimension, dimension, point, dimension, 1); points[i][0] = point[0][0]; points[i][1] = point[1][0]; } } void trans(double tx, double ty) { double T[5][5] = { {1,0,tx},{0,1,ty},{0,0,1} }; double point[5][5]; int i; for (i = 0; i < num; i++) { point[0][0] = 1.0 * points[i][0]; point[1][0] = 1.0 * points[i][1]; point[2][0] = 1; mutiply(T, dimension, dimension, point, dimension, 1); points[i][0] = point[0][0]; points[i][1] = point[1][0]; } } void mutiply(double a[5][5], int ar, int ac, double b[5][5], int br, int bc) { int i, j, k; double c[5][5]; for (i = 0; i < ar; i++) { for (j = 0; j < bc; j++) { c[i][j] = 0; } } for (i = 0; i < ar; i++) { for (j = 0; j < bc; j++) { for (k = 0; k < ac; k++) { c[i][j] += 1.0 * a[i][k] * b[k][j]; } } } for (i = 0; i < ar; i++) { for (j = 0; j < bc; j++) { b[i][j] = c[i][j]; } } } int main() { initgraph(1000, 800); ExMessage m; //绘画初始矩形 setcolor(WHITE); rectangle(points[0][0], points[0][1], points[2][0], points[2][1]); int x0, y0, x1, y1; while (1) { m = getmessage(EX_MOUSE | EX_KEY); switch (m.message) { case WM_LBUTTONDOWN: x0 = m.x; y0 = m.y; //画直线起点 setlinecolor(WHITE); setfillcolor(GREEN); fillrectangle(m.x - 3, m.y - 3, m.x + 3, m.y + 3); break; case WM_RBUTTONDOWN: x1 = m.x; y1 = m.y; //画直线终点 setlinecolor(WHITE); setfillcolor(GREEN); fillrectangle(m.x - 3, m.y - 3, m.x + 3, m.y + 3); //处理直线 line(x0, y0, x1, y1); anysymmetry(x0, y0, x1, y1); paint(); for (int i = 0; i < 4; i++) { points[0][0] = newpoints[0][0]; points[0][1] = newpoints[0][1]; points[1][0] = newpoints[1][0]; points[1][1] = newpoints[1][1]; points[2][0] = newpoints[2][0]; points[2][1] = newpoints[2][1]; points[3][0] = newpoints[3][0]; points[3][1] = newpoints[3][1]; } break; case WM_KEYDOWN: if (m.vkcode == VK_ESCAPE) { return 0; } } } _getch(); closegraph(); return 0; } |