什么是稀疏向量（向量的稀疏表示）

对数据进行预处理时，一般需要对类别型特征进行编码：

序号编码
独热编码
二进制编码
其中独热编码用的是最多的。但是当类别数十分巨大时，独热编码是一个非常稀疏的向量，只有一个值不为0，其他值均为0。可以使用向量的稀疏表示来大大的节省空间，并且目前大多数的算法都接受稀疏向量形式的输入。

举个例子：
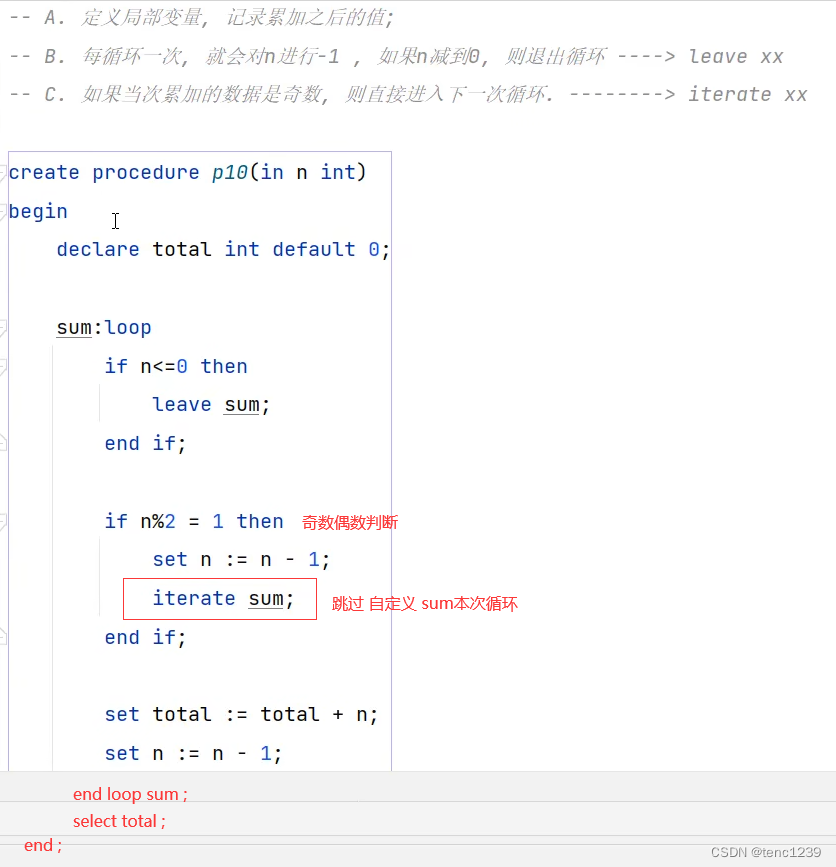
v = [ 0 , 0 , 0 , 0 , 1 , 0 , 3 , 0 , 0 , 0 ]

对于向量 v ，其稀疏表示为
( 10 , [ 4 , 6 ] , [ 1 , 3 ] )

10代表v 的长度，[ 4 , 6 ] 表示非零元素的下标，[ 1 , 3 ] 表示非零元素的值。

准确率和召回率

准确度：正例和负例中预测正确数量占总数量的比例，用公式表示：

$ACC=\frac{TP+TN}{TP+FP+FN+TN}$

召回率 Recall：以实际样本为判断依据，实际为正例的样本中，被预测正确的正例占总实际正例样本的比例。

召回率的另一个名字，叫做“查全率”，评估所有实际正例是否被预测出来的覆盖率占比多少，我们实际黑球个数是3个，被准确预测出来的个数是2个，所有召回率r=2/3。

1、什么情况下精确率很高但是召回率很低？

一个极端的例子，比如我们黑球实际上有3个，分别是1号、2号、3号球，如果我们只预测1号球是黑色，此时预测为正例的样本都是正确的，精确率p=1，但是召回率r=1/3。

2、什么情况下召回率很高但是精确率很低？

如果我们10个球都预测为黑球，此时所有实际为黑球都被预测正确了，召回率r=1，精确率p=3/10。

Precision值和Recall值是既矛盾又统一的两个指标，为了提高Precision值，分类器尽量在更有把握时才把样本预测为正样本，但此时往往会过于保守而漏掉很多没有把握的正样本，导致Recall值降低。

F1 score综合地反映，F1是精准率和召回率的调和平均值。

ROC曲线的横坐标为假阳性率，纵坐标真阳性率。

AUC是ROC曲线下面积的大小，AUC一般在0.5-1之间，越大说明分类器越可能把真正的正样本排在前面，分类性能越好。

训练数据不足

让模型采用特定的内在结构、条件假设或添加一些约束条件；去调整、变换或拓展训练数据，让其展现出更多的更有用的信息。如在图像分类任务中，可对训练集中的每幅图像进行以下变换。

余弦距离

在机器学习问题中，通常将特征表示为向量的形式，所以在分析两个特征向量之间的相似性时，常使用余弦相似度来表示。余弦相似度的取值范围是[-1,1]，相同的两个向量之间的相似度为1。如果希望得到类似于距离的表示，将1减去余弦相似度即 余弦距离。因此，余弦距离的取值范围为[0,2]，相同的两个向量余弦距离为0。

余弦相似度为两个向量夹角的余弦，余弦相似度在高维情况下保持“相同时为1，正交为0，相反为-1” 。余弦距离会认为（1，10）和（10，100）两个距离很近，但显然有很大差异，此时我们更关注数值绝对差异，应当使用欧式距离。

A/B测试

在互联网公司中，A/B测试是验证新模块、新功能、新产品是否有效，新算法、新模型的效果是否有提升，新设计是否受到用户欢迎，新更改是否影响用户体验的主要测试方法。在机器学习领域中，A/B测试是验证模型最终效果的主要手段。

在对模型进行过充分的离线评估之后,为什么还要进行在线A/B测试?

(1)离线评估无法完全消除模型过拟合的影响，因此,得出的离线评估结果无法完全替代线上评估结果。

(2）离线评估无法完全还原线上的工程环境。一般来讲，离线评估往往不会考虑线上环境的延迟、数据丢失、标签数据缺失等情况。因此，离线评估的结果是理想工程环境下的结果。

(3）线上系统的某些商业指标在离线评估中无法计算。离线评估一般是针对模型本身进行评估,而与模型相关的其他指标，特别是商业指标，往往无法直接获得。比如,上线了新的推荐算法，离线评估往往关注的是ROC曲线、P-R曲线等的改进，而线上评估可以全面了解该推荐算法带来的用户点击率、留存时长、PV访问量等的变化。这些都要由A/B测试来进行全面的评估。

超参数调优

一般会采用网格搜索、随机搜索、贝叶斯优化等算法。

超参数搜索算法一般包括：

一是目标函数,即算法需要最大化/最小化的目标

二是搜索范围,一般通过上限和下限来确定;

三是算法的其他参数，如搜索步长。

网格搜索：先使用较广的搜锁范围和较大的步长，来寻找全局最优值可能的位置，然后逐渐缩小搜索范围和步长，但由于目标函数一般是非凸的，所以很可能错过全局最优值。

随机搜索：理论依据是如果样本点集足够大，那么随机采样也能大概率找到全局最优值或其近似值。一般笔网格搜锁快。

贝叶斯优化算法：容易陷入局部最优值。