（3）Density Map Estimation（主流）

这是crowd counting的主流方法

传统方法不好在哪里？object detection-based method和regression-based method无法从图像中提取更抽象的有助于完成人群计数任务的语义特征

概况：给每个像素赋予密度值，总和记为场景中的人数。用高斯核gaussian kernel来模拟simulate人头在原图的对应位置corresponding position，然后去做由每一个高斯核组成的这个矩阵正则化perform normalization in matrix ，we use a gaussian kernel to simulate a head in corresponding position of the original image. After do this action for all heads in the image, we then perform normalization in matrix which is composed by all these gaussian kernels.；学习局部特征和目标密度图之间的映射 learning the mapping between local features and object density maps.，这个映射可以使用random forest regressor来学习这种非线性的映射 learn the non-linear mappings.

定义：

从过程的角度：（1）建立局部位置的特征和目标映射图之间的映射关系is a method to solve this problem by learning a linear mapping between features in the local region and its object density maps_我猜—既然涉及局部，可以解决没有空间信息的问题了（2） 同时这个过程也整合了学习过程中的显著性这一数据It integrates the information of saliency during the learning process（3）这个从图片到density map过程怎么做：用随机森林回归做非线性映射 use random forest regression to learn a non-linear mapping instead of the linear one.（为什么用随机森林回归，随机森林回归有什么特性，满足了你们的需求？；随机森林回归为什么是非线性的）

从人数counting结果这个角度：the density functions in our approaches are real-valued functions 对每一个像素格子做计算over pixel grids, 每个区域的值做积分，得到就是图片中人的数量whose integrals over image regions should match the object counts

1. 优势：（1）提高模型的学习能力，容易克服人群遮挡的问题（2）density map提供的信息更多，既提供了图片中人的数量这个信息，还提供了人分布在哪些区域、每个区域多少人的分布信息： be able to localise the crowd.，但是这种定位不是通过精细化识别每个个体来获得，因为图中人多的地方用密度点表示，颜色越重的这个patch人越多，但是只有这个区域的人数，不知道这个人的头在哪、手在哪、腿在哪，They do not focus on explicitly detecting each individual.（3）比起regression method 解释性更强

2. 劣势：泛化能力差，对于训练数据中人群的分布依赖性较强

生成density map有三种方法

（1）Fixed-size density map.对于每个头，都使用相同大小的高斯核来模拟头的位置Use the same gaussian kernel to simulate all heads.这个方法仅适用于，照片中所有的人距离镜头的远近都差不多的情境下。我们想象一下，距离镜头近的人，在照片中头颅的大小就会更大吗；距离镜头远的人，在照片中的头颅就会偏小；这种现象称为perspective distortion。应对这种场景，我们应该给离镜头近、头看着大的人分配一个更大的高斯核，我们应该给距离镜头远、头看着小的人分配一个更小的高斯核。因此就出来了下面这两种方法。This method applies to scene without severe perspective distortion.

（2）Perspective透视 density map（根据透视图调整人头大小）：用行人的身高做线性回归enerated by linear regression of pedestrians' height，来生成对于不同脑袋大小的不同size的高斯核generate gaussian kernels with different sizes to different heads。我猜，透视图指的是，近处的人的平均身高我提供给你，远处人的平均身高我也给你，你根据这个远处和近处人的身高比例，对于人头大小进行调整，也就是对高斯核进行调整。代表作：https://www.ee.cuhk.edu.hk/~xgwang/papers/zhangLWYcvpr15.pdf

（3）KNN density map.使用K近邻算法去生成不同大小脑袋的不同大小的高斯核。这种方法适用于极度拥挤的场景。代表作：https://www.semanticscholar.org/paper/Single-Image-Crowd-Counting-via-Multi-Column-Neural-Zhang-Zhou/2dc3b3eff8ded8914c8b536d05ee713ff0cdf3cd?p2df

也有用CNN-based aproaches去预测密度图的，因为its success in classification and recognition

可以用

（S1）输入图像，输出一张与输入一样大小的人群密度图，

生成密度图的过程就是将只有0和1的矩阵经过高斯卷积计算得出的。

Xi为每个人头标注点的二维坐标位置，在像素点xi处如果有人头（xi表示的是(x,y)在图片上的二维坐标），我们将其表示为函数δ(x−xi)，即当x=xi，δ(x−xi)=1；x≠xi，δ(x−xi)=0，其他地方全为0的函数，H(x)就是一个只有0或1的矩阵。那么，一张图有N个人头的话，可以描述为下列函数H(x)。具有N个人头的标签可以表示为H（x）。

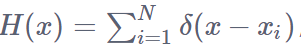
为什么输入信号卷积冲激响应就能得到输出信号？ - Zhu Xuxx的回答 - 知乎https://www.zhihu.com/question/39753115/answer/1475105933

H(x）是冲激函数求和得来的。 $$\delta$$这个函数，是冲激函数，输入的只要不是0，输出都是0，输入如果是0，输出就是1.上面把输入改成了 $$x-x_{i}$$。（疑问，如果输入两个0，那输出还是1啊？）

在 H(x) 中的密度图（H(x)就是dot map）是离散的，为了将其转化为连续函数（我对这个表示怀疑），我们拿着高斯函数G(x)对H(x)做卷积运算 进行平滑。然后我们拿着二维高斯核函数G(x,y)对H(x)进行卷积运算，得到F(x)。为了将H(X)转为一个连续密度函数，使用高斯核Gσ，密度可以描述为F(x)，σ是指的standard deviation

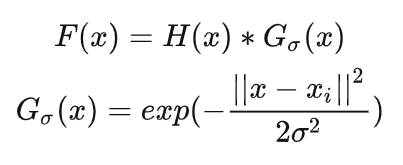
在图像处理中一般使用的高斯函数获取高斯核模版，需要给定相应的参数：高斯核大小 ksize (奇数)，和标准差 σ 。生成一个大小为 ksize 大小的模版，整个模版和为1，有中心到远离中心像素点的值的大小逐渐减小。

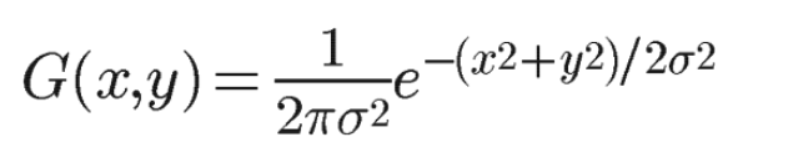
$$\sigma$$是可以调节的参数，决定了从一个点向外blur 摊开的面积，可以理解为头的大小。x,y为相对于中心点的坐标参数

有一个计算高斯卷积过程的例子：https://blog.csdn.net/erkey/article/details/127500631

高斯核函数G(x,y)的输入是二维坐标(x,y)。下面第二行、第三行的公式中的x，表示的其实是(x,y)这个二维坐标

为什么要使用高斯核函数？

讲解很深入的文章：运行代码指导：https://blog.csdn.net/qq_40356092/article/details/108140273

高斯核做卷积运算的数学原理讲的更深入的：https://zhuanlan.zhihu.com/p/566375016

论文原文：ICCV2019 Adaptive Density Map Generation for Crowd Counting （ADMG）在过去的方法中，密度图一旦制作完成就不再去修改；该论文提出了一种在训练过程中微调密度图的方法。

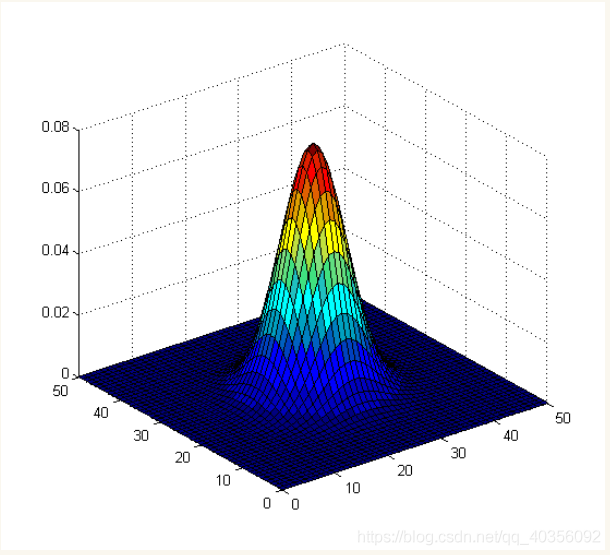
高斯核函数是一个正态分布钟形线，坐标越趋近中心点，值就越大，反之越小。也就是说离中心点越近权值就越大，离中心点越远，权值就越小。使用高斯函数，是因为有下面这个场景

  在真实图片中，每个人头是具有一定大小的，对应图片中的一小片区域。但是，数据集提供的标注的点信息只能提供位置信息，并不能提供人的尺度信息（哪一片是脑袋）。但是在数据标注annotation文件中，我们这样来标注一个“头”，将矩阵中一个像素点的坐标的值设定为1来表示这个人头，这个坐标以外其他的点如果不是“人头”就标注为0。这显然是十分不合理的，因为一个人头不可能只占据一个像素点的面积，而应该是一片区域。非0即1的像素级标签显然不符合卷积神经网络的特性，我们需要用高斯核，来使得标签在空域变得平滑一些呢。换句话说，我们通过将点信息通过高斯模糊转换为密度图信息对于网络的训练可以提供更多的监督信息。各种各样的模型其实做的是，通过各种方式建立原图像与密度图之间的映射关系

  （第一步）比如下面这个图，本来标注的时候只有中心这个一个点标注了有人头，为1，其他周围的八个点都是0，没有人头。我拿着你规定好的高斯卷积核对中间一个1其他全是0的这个矩阵做卷积运算，最终得出下面这个图，八个本来是0的位置也有了数值

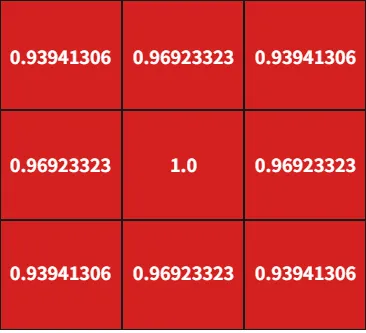
  （第二步）计算出9个格子的和，然后上图每个格子都除以和，得出一个值。这样九个格子的和就是1了。这样就满足“对density map整个做积分等于图中所有人数”这一要求了。

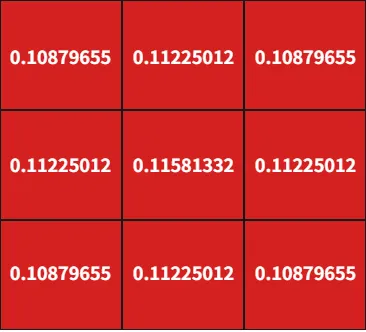
  如何解决呢？我们使用高斯核函数将这个中心点的像素值用它周围点的像素值的加权平均代替，周围像素点的权值相加起来等于1。我们将这个像素点（数值为1的这个点）这个“1”这个值摊开，使得这个像素点周围一定半径的像素点也是有数值的（而不是设定为0）。至于摊多么大面积呢，由δ决定，摊开多大体现了我们认为一个人的“脑袋”有多大。——这样做的好处：既不影响生成的密度图中总人头数，又能够比较真实的反应每个人头在空间里面的位置特征（就是这个脑袋在什么位置、占了多大面积）。

这个σ可否不fixed,是否可以自适应的确定呢？

为什么要在一张图片里使用不同的σ？：——我们需要考虑到透视畸变对人头大小的影响。透视畸变指的是，在拍摄照片时，距离镜头越远的物体在照片上显得越小，占用的空间像素点较少；距离镜头近的人头较大，占用的空间像素点较多。所以在使用高斯核函数时需要根据不同人头大小设置不同的模糊半径，即根据图像中每个人头部大小来确定参数σ，这样制作出的密度图更加精细。

怎么做：但是在实际情况下，我们不可能准确的获得每个头部的尺寸大小，那么我们可以找到什么替代的数据呢？用这个人头与相邻人头中心点的距离来等价代替“人头的尺寸大小”这一数据。因为人头尺寸越大的情况下，人头之间的距离往往越大。比如下面这幅，打黄框，下面有一个女士，上面也有一个女士。明显可以看到下面这个女士距离镜头近，所以头大；上面那个女士距离镜头远，所以头小。而下面这个女士的头距离周围人脑袋的距离大于上面那个女士。因此这个等价替换是合理的。

在拥挤场景中，我们可以使用相邻k个人头与该人头的平均距离来作为高斯核函数的参数σ，这样就能够更好地表示人头大小的特征信息。确定这个脑袋和附件的k个其他脑袋的距离使用“KDTree”这个模型

这个 $$\sigma$$随着情况变的高斯核被称为自适应高斯核（geometry-adaptive kernels）（每个人头的高斯核会根据自身与临近人头之间的距离进行自适应的变化）

但是也有一些研究者在一些数据集上采用固定的 $$\sigma$$比如下面这些数据集，他们的照片中人的脑袋可能大小都比较接近所以用了相同的 $$\sigma$$,比如 15 10 3

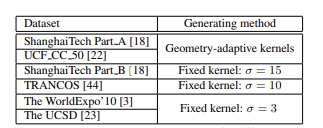
在生成密度图时涉及到的参数还有k（相邻k个人头的平均距离），以及系数beta，在进行人群计数时可以根据不同的数据集进行改变和调参。

几何适应高斯核(Geometry-adaptive Kernels)

这个东西是用来制作ground truth标签label的。你拿到一张图，图里面每个点表示人头所在的位置，成为dot map。然后你拿着这个高斯核把这张点图，转化为density map图，也就是ground truth。

高斯核的大小可以根据位置自动化的调整。为了使得密度图能够更好地与不同视角（[1]距离相机近，头大；距离相机远，头小;[2]不拥挤的场景，人的头部往往更大；极度拥挤的场景，人的头部往往更小。）且人群很密的图像对应起来，我们对传统的基于高斯核(Gaussian Kernel)的密度图做了改进，提出了基于几何适应高斯核(Geometry-adaptive Kernels)的密度图

其中参数是σ，作用是控制函数的径向作用范围。根据图像中每个人的头部大小确定传播参数σ。发现人头大小通常与拥挤场景中两个相邻人的中心之间的距离有关。不拥挤的场景，人的头部往往更大；极度拥挤的场景，人的头部往往更小。对于那些拥挤场景的密度图，通常根据每个人与邻域的平均距离来自适应地确定每个人的传播参数（确定这幅图中人头部的大小）。

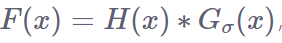
然后拿着这个平均距离 $$\bar{d^{i}}$$乘以一个系数 $$\beta$$,得到这个传播参数 $$\sigma$$（也是高斯核的标准差）

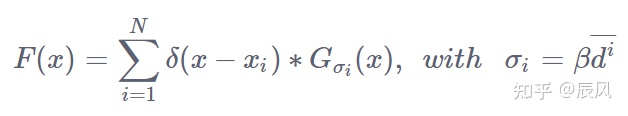
对于参数 $$\sigma_{i}$$里面的 $$\overline{d_{i}}$$是怎么回事，这里说明一下。有 $$i$$个人头，对于图像中给定的每个头部xi，我们定义到每个头颅最近的 $$k$$个（ $$m$$个）头颅的距离的集合为 $$d_{i}$$， $$d_{i}$$第一个元素表示距离这个人头最近的那个头到这个头的距离。然后把这一堆距离取个平均，得出平均距离 $$\bar{d_{i}}$$

缺点：无法给出准确的人的位置信息（我不认同这句话）

拿到了密度图density map，如何得出人数？

训练过程，输入是原图像，输出是密度图，通过对比ground truth密度图和你预测的密度图来做反向传播优化模型。测试过程就是输入图像，输出预测的密度图。至于人数，密度图的积分就是人数。

在整个过程中使用了三个数据： image，dot Map, density Map。image是原图。dot Map是把原图上的人头都用dot标注下来的annotation图。density map是用高斯核对dot Map做卷积得来的。

有另一种描述方式：

https://zhuanlan.zhihu.com/p/59764673

Learning To Counting Objects in Images

Regression-based model：把图片放进一个特征提取器里面，然后将提取到的特征，丢入回归模型中，进而得到人数，用数学公式的话是下面这样的表示

Density map model——整个过程——:先把原图$$I $$丢进$$\phi$$里面得到提取好的特征 $$x_{p}$$,然后通过把 $$x_p$$乘以矩阵 $$w$$做一个投影，从一些特征映射出一个density map,这个过程被称作 $$F(x_{p})$$，同时这也是密度图的结果。然后拿着特征图 $$F(x_{p})$$来做积分1求和得到 $$c$$，这个 $$c$$就是图片中人的数量。

$$\huge x_{p} = x_{p}\phi(I) \\ F(x_{p}) = w ^\mathrm{T} x_{p} \\ c = \sum _{p} ^ {} F(x_{p})$$

构造density map的方法

我也不知道为什么下一步就是求解这个，我也不知道loss function为什么就是这个样子。我估计下面这个不是loss function，而是另外一个东西——他应该是笔误了

（第一种）平方求和——MSE, mean squared erroe

真正的loss function应该是下面这个，预测的和真实的差别才是loss function

（第二种）绝对值求和

是先将density map上的值求和，再计算 LP Metric，这样本质上属于公式(1)的建模方式，忽略了人工标注的位置信息：(不知道说的是啥意思。我不认同他的观点。只是度量的方式一个是平方，一个是绝对值，和是否引入人工标注的信息没关系）

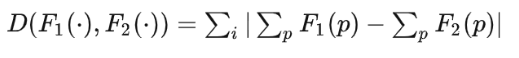
基于上述2种loss的缺陷，Victor提出了MESA distance：

  其中，B指density map上所有子区域(subarray)

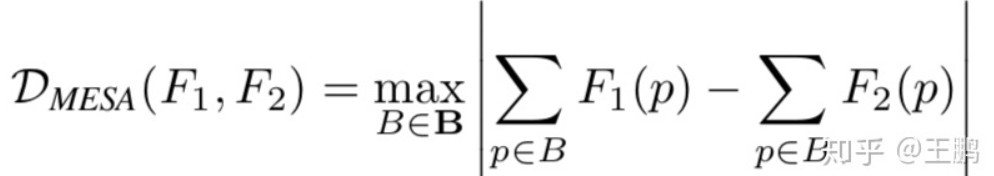
随机森林density map

不知道哪篇论文，博客看见的https://blog.csdn.net/uestcbyl/article/details/82970670

文章提到没有一种单独的方法可以计算低分辨率、严重遮挡、透视和透视导致的图片记数问题，发现了一种数学空间关系，可以约束邻近区的计数估计，因此通过将拥挤人群看成不规则非均匀的纹理，使用傅里叶分析和头部检测，并在邻近筛选信息点，通过傅里叶，信息点，和头部检测进行结合，在局部的补丁内进行计算，并在一个多尺度的MRF框架内进行全局约束（没看懂）

当遇到稀疏和不平衡的数据时，提出了学习回归模式的累积属性表示，将特征映射到一个累积的属性空间内。

（4）Deep Learning based methods

比任何传统的方法都好， achieve better accuracy over the other above discussed conventional approaches

前面三种方法都可以用深度学习来替代他们原本的机器学习方法，就得到了基于深度学习的行人检测/人数回归/人群密度估计方法

优势

（1）深度学习网络的复杂程度决定了它的学习能力/记忆能力更强,

（2）在数据量足够充足的前提下，深度学习模型的泛华能力更强。深度学习之前的模型，其训练集和测试集基本都是将同一个场景中的一段视频分为两部分，一部分训练，另一部分测试，如果跨场景测试，结果不堪入目。而引入深度学习后，现在的人群密度估计方法都是跨场景的，结果还可以，测试集中的场景都是千变万化的，更为符合日常应用中的模式。

（3）在监控视频的人群计数算法中，前景分割是不可或缺的步骤，然而前景分割本事就是一个比较困难的任务，算法性能很大程度地受其影响。卷积神经网络实现了端对端训练，无需进行前景分割以及人为地设计和提取特征，经过多层卷积之后得到的高层特征(High-level Features)使得算法性能更加优秀。