前言

此篇文章为MATLAB矩阵运算笔记，需要先学习线性代数的知识，一些线性代数概念性的知识，本文章不再说明。

一、矩阵的输入与结构操作

1-1 矩阵输入

例1-1：输入矩阵值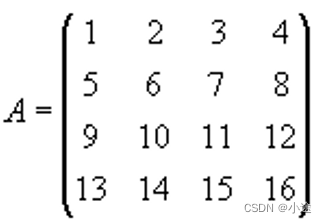

A=[1 2 3 4; 5 6 7 8; 9 10 11 12; 13 14 15 16]

1-2 矩阵扩充

（1）扩充行

% 例如扩充例1-1矩阵
A(5,:)=[17 18 19 20]在第五行添加17 18 19 20


%｛
% 运行结果：
% A =
% 
%    1     2     3     4
%    5     6     7     8
%    9    10    11    12
%   13    14    15    16
%   17    18    19    20
% ｝%

（2）扩充列

%例如扩充例1-1列
A(:,5)=[10,20,30,40]

%运行结果略。。。

（3）其他命令

A(m, n)%提取第m行，第n列元素
A(:, n)%提取第n列元素
A(m, :)%提取第m行元素
A(m1:m2, n1:n2)%提取第m1行到第m2行和第n1列到第n2列			的所有元素
A(m:end, n)	%提取从第m行到最末行和第n列的子块
A(:)%得到一个长列矢量，该矢量的元素按矩阵的列进行排列

对于上三角、下三角部分和主对角线上的元素可以用以下命令：

triu(A)%提取矩阵A的上三角部分
tril(A)%提取矩阵A的下三角部分
diag(A)%提取矩阵的主对角线上的元素

对于矩阵的翻转和旋转，可以使用下述命令

fliplr(A)%矩阵A左右翻转
flipud(A)%矩阵A上下翻转
rot90(A)%矩阵A整体逆时针旋转90°

（4）矩阵的修改和元素的删除

A(2,:)=[] %删除第二行元素
A(1,1)=0 %将第一行第一列元素修改为‘0’

1-3 特殊矩阵生成

zeros(m,n)%生成一个mXn的零矩阵
ones(m,n)%生成一个元素都是1的mXn的矩阵
eye(n)%生成一个n阶单位矩阵
rand(m,n)%生成一个mXn的随机矩阵
vander(V)%生成一个以向量V为基础向量的范蒙德矩阵
magic(n)%生成一个n阶魔方矩阵
hilb(n)%生成一个n阶希尔伯特矩阵
invhilb(n)%求n阶希尔伯特的逆矩阵

二、矩阵的计算

2-1 、矩阵的基本运算

如果已经输入了矩阵A和B，则可由下述命令对其进行运算

A' %矩阵的转置
K*A %数K乘以A
inv(A) %A的逆矩阵
A\B %A的逆矩阵乘以B
A+B %加法
A*B %乘法
A^x %A的x次方
B/A %B乘以A的逆矩阵

2-2、线性方程组的求解

在MATLAB中有很多求解线性方程组的方法，本文就举两个命令

rref(A) %A的最简行阶梯矩阵
bull(A,'r') %求解齐次线性方程组 Ax=0

2-3、矩阵的特征值

矩阵的特征值与特征向量在矩阵的相似对角化和求解微分方程组等问题广泛应用，在MATLAB直接输入命令即可直接求解

f=Poly(A) %f为A的特征多项式
lambda=roots(f) %计算多项式f的全部根

参考文献
[1] 王东、赵海霞.线性代数.北京：北京大学出版社，2020年1月第1版