说明

闵老师的文章链接：日撸 Java 三百行（总述）_minfanphd的博客-CSDN博客
自己也把手敲的代码放在了github上维护：https://github.com/fulisha-ok/sampledata

day39 关键路径

1.关键路径

AOV网顶点表示活动的网络，且每个活动是有前驱和后继关系存在的。
AOE网用边表示活动的网络，顶点表示事件，有向边表示活动，边上的权值表示完成活动需要的时间
从开始节点到到各个顶点所有路径中，最大路径长度的路径是关键路径（一般简单的图可以直接看出来那些是关键路径，但是复杂的就需要进行计算了）求关键路径过程中会涉及事件（顶点）Vi最早发生时间和最迟发生时间；活动（边）最早发生时间和最迟发生时间。
结合一个例子来说明。（例子网上找的）
在求关键路径时，把每个顶点（事件）的最早和最晚发生时间算出，如果最早和最晚相等即可求出关键路径。去计算活动最早和最晚发生时间进而可以求出关键路径上的关键活动。

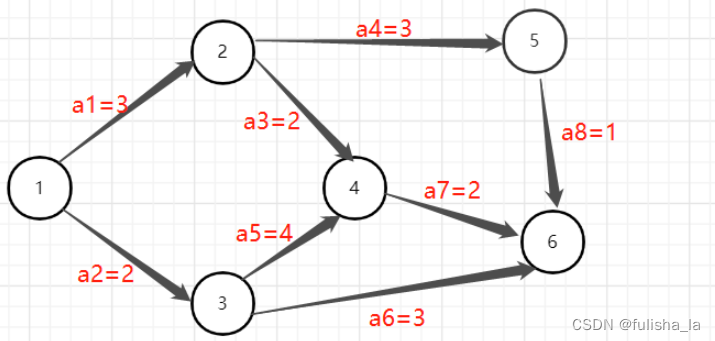
如图为各个顶点的最早最晚发生时间：
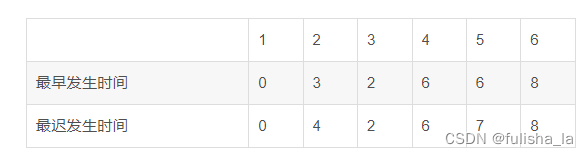
在这里插入图片描述
关键路径上的节点：1，3，4，6

各个活动的最早最晚发生时间（结合顶点的最早和最晚好观察些）：
a1,a2最早开始时间看1节点最早时间,a3最早开始时间看2最早开始时间…a7看节点4最早时间
a1看节点2最迟发生时间是4,4-3=1，a2看节点3最迟发生时间2-2=0…a7看节点6最迟发生时间8-2=6

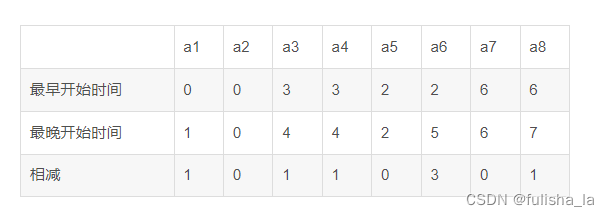
在这里插入图片描述
关键活动为a2->a5->a7

2. 代码分析

1.算出各个节点的入度，找到入度为0的节点
2.从入度为0节点开始，到每个顶点的最早开始时间，并用数组记录（注意：有多个顶点汇聚到一个顶点，要找其中最大的那个最为最早开始时间。这就好比组装车，a组装发动机，b组装车身底盘，c组装车架，只有三者都完成，才能开始进行d 组装整个车，d最早开始时间要看a,b,c中最晚时间）
3.算出各个节点的出度，找到出度为0的节点，
4.从出度为0的节点开始，到每个顶点的最晚开始时间，在拓扑排序是正着找入度为0的就移除掉这个顶点，接着再找入度为0的，再这里我们可以将拓扑排序反着来，找出度为0再移除，这样我们就能去找最晚时间。节点最晚时间是看这个节点所有的后继节点到终点最长的的时间那个。

 /**
     * Critical path. Net validity checks such as loop check not implemented.
     * The source should be 0 and the destination should be n-1.
     */
    public boolean[] criticalPath(){
        //One more value to save simple computation.
        int tempValue;

        //step1. the in-degree of each code
        int[] tempInDegrees = new int[numNodes];
        for (int i = 0; i < numNodes; i++) {
            for (int j = 0; j < numNodes; j++) {
                if (weightMatrix.getValue(i, j) != -1) {
                    tempInDegrees[j]++;
                }
            }
        }
        System.out.println("In-degree of nodes: " + Arrays.toString(tempInDegrees));

        //step2 Topology sorting
        int[] tempEarliestTimeArray = new int[numNodes];
        for (int i = 0; i < numNodes; i++) {
            if (tempInDegrees[i] > 0) {
                continue;
            }
            System.out.println("Removing " + i);

            for (int j = 0; j < numNodes; j++) {
                if (weightMatrix.getValue(i, j) != -1) {
                    tempValue = tempEarliestTimeArray[i] + weightMatrix.getValue(i, j);
                    if (tempEarliestTimeArray[j] < tempValue) {
                        tempEarliestTimeArray[j] = tempValue;
                    }
                    tempInDegrees[j]--;
                }
            }
        }

        System.out.println("Earliest start time: " + Arrays.toString(tempEarliestTimeArray));

        //step3.The out-degree of each node.
        int[] tempOutDegrees = new int[numNodes];
        for (int i = 0; i < numNodes; i++) {
            for (int j = 0; j < numNodes; j++) {
                if (weightMatrix.getValue(i, j) != -1) {
                    tempOutDegrees[i]++;
                }
            }
        }
        System.out.println("Out-degree of nodes: " + Arrays.toString(tempOutDegrees));

        //step4. reverse topology sorting
        int[] tempLatestTimeArray = new int[numNodes];
        for (int i = 0; i < numNodes; i++) {
            tempLatestTimeArray[i] = tempEarliestTimeArray[numNodes - 1];
        }

        for (int i = numNodes -1; i >=0; i--) {
            // This node cannot be removed.
            if (tempOutDegrees[i] > 0) {
                continue;
            }
            System.out.println("Removing " + i);

            for (int j = 0; j < numNodes; j++) {
                if (weightMatrix.getValue(j, i) != -1) {
                    tempValue = tempLatestTimeArray[i] - weightMatrix.getValue(j, i);
                    if (tempLatestTimeArray[j] > tempValue) {
                        tempLatestTimeArray[j] = tempValue;
                    }
                    tempOutDegrees[j]--;
                    System.out.println("The out-degree of " + j + " decreases by 1.");
                }
            }

        }
        System.out.println("Latest start time: " + Arrays.toString(tempLatestTimeArray));
        boolean[] resultCriticalArray = new boolean[numNodes];
        for (int i = 0; i < numNodes; i++) {
            if (tempEarliestTimeArray[i] == tempLatestTimeArray[i]) {
                resultCriticalArray[i] = true;
            }
        }

        System.out.println("Critical array: " + Arrays.toString(resultCriticalArray));
        System.out.print("Critical nodes: ");
        for (int i = 0; i < numNodes; i++) {
            if (resultCriticalArray[i]) {
                System.out.print(" " + i);
            }
        }
        System.out.println();

        return resultCriticalArray;
    }

在求关键路径的代码中，计算每一个结点的入度和出度，这还是比较简单，只是赋值的时候是i还是j有区别;计算每一个结点最早开始时间（tempEarliestTimeArray）采用拓扑排序思想，计算每一个结点最晚开始时间（tempLatestTimeArray）采用逆拓扑排序思想；在实现关键路径代码的过程中，每一个步骤都是清晰明了，他们之间的耦合性不大。在求节点最早和最晚时间时，用拓扑排序思想（正反）去求解这个思路学习到了。这突然让我想到Day26写的后序遍历算法，结合栈采用逆向思维输出~

单元测试
虽然代码几个循环就写出来，我还是准备根据代码debug出相应的过程更容易去理解。
根据测试中画出的图例（在线画图工具）

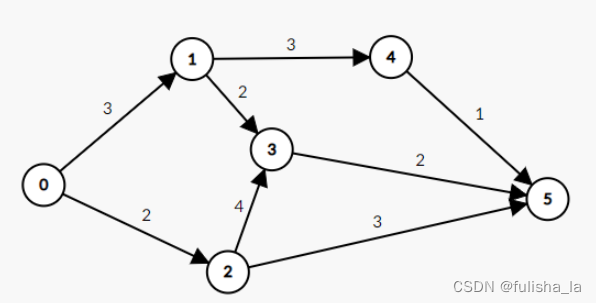
根据图例画出矩阵：
$\begin{array}{c} % 总表格 \begin{array}{c|cccc} % 第二行 Delta 值数组 \Delta & 0 & 1 & 2 & 3 & 4 & 5\\ \hline 0 & -1 & 3 & 2 & -1 & -1 & -1 \\ 1 & -1 & -1 & -1 & 2 & 3 & -1 \\ 2 & -1 & -1 & -1& 4 & -1 & 3 \\ 3 & -1 & -1 & -1 & -1 & -1 & 2 \\ 4 & -1 & -1 & -1 & -1 & -1 & 1\\ 5 & -1 & -1 & -1 & -1 & -1 & -1 \\ \end{array} % 第二行表格结束 \end{array} % 总表格结束$
1.各结点的入度
2.从入度为0节点开始，到每个顶点的最早开始时间，并用数组记录
3…算出各个节点的出度，找到出度为0的节点，
4.从出度为0的节点开始，到每个顶点的最晚开始时间
算出最晚和最早相等的